[人工智能]Apollo规划代码ros移植-混合A*

前言

今天学习移植一下混合A*（Hybrid a）。想要工程代码的看我这一篇：
Apollo6.0规划代码ros移植-路径规划可跑工程分享

原理基础

1.A start算法
使用A Star 算法实现自动寻路详解

2.Rs曲线
Reeds-Shepp和Dubins曲线简介

[运动规划算法]Dubins曲线和Reeds-Shepp曲线

流程

Hybrid A star是一种带有半径约束的路径平滑规划算法，算法思想来自A算法，但A是没有考虑平滑和半径约束的路径规划算法，且基于栅格地图的网格搜索算法，它们的目标代价函数是为了形成一条路径最短的无碰撞路径。而HybirdAstar是在二者的基础上加入半径约束，进行路径不同曲率方向采样，同时采用reedsheep曲线，进行目标点的衔接，来加速路径的生成效率。
plan代码：

// Hybrid A star的核心过程
//输入：起点（sx, sy, sphi）、终点（ex, ey, ephi）、地图边界（XYbounds，好像要4个：xmin, xmax, ymin, ymax）、障碍物顶点信息（obstacles_vertices_vec）
//输出：*result
bool HybridAStar::Plan(
    double sx, double sy, double sphi, double ex, double ey, double ephi,
    const std::vector<double> &XYbounds,
    const std::vector<std::vector<Vec2d>> &obstacles_vertices_vec,
    HybridAStartResult *result)
{
    // clear containers
    //每次规划，清空之前的缓存数据
    open_set_.clear();
    close_set_.clear();
    open_pq_ = decltype(open_pq_)();
    final_node_ = nullptr;

    std::vector<std::vector<LineSegment2d>> obstacles_linesegments_vec;
    //构造障碍物轮廓线段容器
    for (const auto &obstacle_vertices : obstacles_vertices_vec)
    {
        size_t vertices_num = obstacle_vertices.size(); // 拿到每个障碍物的边
        std::vector<LineSegment2d> obstacle_linesegments;
        //我认为这里有错，少构造了一条线段
        for (size_t i = 0; i < vertices_num - 1; ++i) // 依次对该障碍物的每个边读取
        {
            LineSegment2d line_segment = LineSegment2d(obstacle_vertices[i], obstacle_vertices[i + 1]); // 遍历各个顶点得到边，这里应该少了end至start的情况
            obstacle_linesegments.emplace_back(line_segment);
        }
        //因为我觉得有问题，所以补充了一条线段
        LineSegment2d line_segment = LineSegment2d(obstacle_vertices[0], obstacle_vertices[vertices_num - 1]);
        obstacle_linesegments.emplace_back(line_segment);

        obstacles_linesegments_vec.emplace_back(obstacle_linesegments); // 该障碍物的所有边得到
    }

    obstacles_linesegments_vec_ = std::move(obstacles_linesegments_vec);

    // load XYbounds
    XYbounds_ = XYbounds;
    // load nodes and obstacles
    //构造规划的起点和终点，并检查其有效性
    start_node_.reset(new Node3d({sx}, {sy}, {sphi}, XYbounds_));
    end_node_.reset(new Node3d({ex}, {ey}, {ephi}, XYbounds_));

    if (!ValidityCheck(start_node_))
    {
        std::cout << "start_node in collision with obstacles";
        return false;
    }
    if (!ValidityCheck(end_node_))
    {
        std::cout << "end_node in collision with obstacles";
        return false;
    }

    //使用动态规划DP来计算目标点到某点的启发代价（以目标点为DP的起点）
    //生成graph的同时获得了目标点到图中任一点的cost，后续只需要查表，空间换时间
    grid_a_star_heuristic_generator_->GenerateDpMap(ex, ey, XYbounds_,
                                                    obstacles_linesegments_vec_);

    // std::cout << "map time " << Clock::NowInSeconds() - map_time;
    //  load open set, pq
    open_set_.emplace(start_node_->GetIndex(), start_node_);
    open_pq_.emplace(start_node_->GetIndex(), start_node_->GetCost());

    // Hybrid A* begins
    size_t explored_node_num = 0;
    double heuristic_time = 0.0;
    double rs_time = 0.0;
    while (!open_pq_.empty())
    {
        // take out the lowest cost neighboring node
        const std::string current_id = open_pq_.top().first;
        open_pq_.pop();
        std::shared_ptr<Node3d> current_node = open_set_[current_id];
        // check if an analystic curve could be connected from current
        // configuration to the end configuration without collision. if so, search
        // ends.
        // true：如果生成了一条从当前点到目标点的ReedShepp曲线，就找到了最短路径
        // false：否则，继续Hybrid A*扩展节点
        if (AnalyticExpansion(current_node)) // 用RS曲线试试运气，运气爆棚可以到达终点，则搜索结束
        {
            break;
        }
        close_set_.emplace(current_node->GetIndex(), current_node);
        // 从current_node出发，依次以不同steering，前进arc(对角线长度)
        for (size_t i = 0; i < next_node_num_; ++i)
        {
            //一个grid内的最后一个路径点叫node，该grid内可以有多个路径点，
            //该node的next_node一定在相邻的其他grid内
            std::shared_ptr<Node3d> next_node = Next_node_generator(current_node, i);
            // boundary check failure handle
            if (next_node == nullptr)
            {
                continue;
            }
            // check if the node is already in the close set
            if (close_set_.find(next_node->GetIndex()) != close_set_.end())
            {
                continue;
            }
            // collision check, 负责碰撞检测，输入参数节点所连接的、在同一grid内的其他路径点也一起检测了
            if (!ValidityCheck(next_node))
            {
                continue;
            }
            // 从未被探索，进行初始化
            // open_set_其实是close_set_和 open_pq_的合集
            // 每个栅格的index由 x_grid_、y_grid_、phi_grid_共同决定，而不只是x_grid_、y_grid，
            // 不过这里phi_grid_根据 phi_grid_resolution 做了离散化，所以重叠程度还是有的
            if (open_set_.find(next_node->GetIndex()) == open_set_.end())
            {
                explored_node_num++;
                CalculateNodeCost(current_node, next_node);
                open_set_.emplace(next_node->GetIndex(), next_node);
                open_pq_.emplace(next_node->GetIndex(), next_node->GetCost());
            }
        }
    }

    if (final_node_ == nullptr)
    {
        std::cout << "Hybrid A searching return null ptr(open_set ran out)";
        return false;
    }

    if (!GetResult(result))
    {
        std::cout << "GetResult failed";
        return false;
    }

    return true;
}

输入：
起点（sx, sy, sphi）、终点（ex, ey, ephi）、地图边界（XYbounds，好像要4个：xmin, xmax, ymin, ymax）、障碍物顶点信息（obstacles_vertices_vec）。
输出：
HybridAStartResult *result

struct HybridAStartResult
{
    std::vector<double> x;
    std::vector<double> y;
    std::vector<double> phi;
    std::vector<double> v;
    std::vector<double> a;
    std::vector<double> steer;
    std::vector<double> accumulated_s;
};

流程代码注释挺清楚的。

测试效果

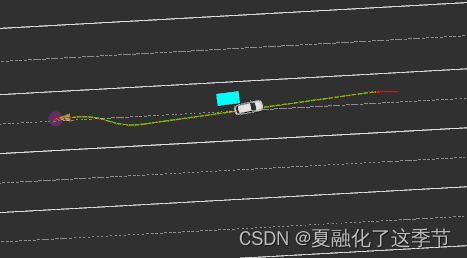
1.第一种可以直接在道路上测试，为了好看，可以关闭Map话题，只开地图的话题：

视角为Orbit(rviz):

定义的起点和终点在同一车道

2.第二种可以切换打开Map的话题，关闭地图的话题，视角为TopDowmOrtho，这时可以出现open_sapce的地图：

open_sapce的地图可以在src/planning/dynamic_routing/maps/map.yaml里面修改图片路径。图片出自https://github.com/karlkurzer/path_planner，感谢大佬。

这里提一下，图里面的黑色原本是障碍物，但是我没有去读里面障碍物的信息，而是用map_empty自己去加障碍物。于是有了下面：

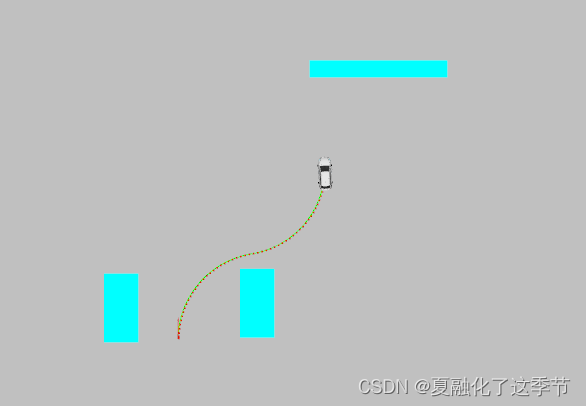
顺便订阅混合A星专用障碍物测试。障碍物发布在src/planning/dynamic_routing/src/Obstacle/Obstacle.cpp文件中。

待修复的bug

1.调用jerk优化的时候，轨迹的纵向长度如果超过26的话（grid的尺寸是1），会求解失败，这是为啥，哪个参数影响，从原理上想还是没想明白，目前还在学习。希望有人可以指导！
我目前先尝试另外的优化公式：
wSmoothness * (xim2 - 4 * xim1 + 6 * xi - 4 * xip1 + xip2);
利用后面2个点，当前点，前面2个点，5个点去优化。
出自：
https://github.com/karlkurzer/path_planner
话说回来，不调用jerk优化，低速的大多数情况也可以跑。

2.用stanly控制不能多段倒车，可能得换个控制算法，目前要换成lqrd, 但是，据说
LQR前提假设：
1，小角度转向，故规划路径的曲率不能变化过快；
2，认为车速恒定，故加速度不能过大或过小，加速度尽可能小；

所以低速可能用不了。。。

参考链接

感谢下面的大佬们，大家原理和代码可以参考这些一起学习。
Apollo 6.0 的 Hybrid A star planner

Baidu Apollo代码解析之Open Space Planner中的Hybrid A*

HybirdAstar算法原理

基于Hybrid A*和ReedSheep曲线的Open Space规划器