开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 面向优化科学研究领域的软件包 -> 正文阅读

[人工智能]面向优化科学研究领域的软件包

面向优化科学研究领域的软件包

项目介绍

??optimtool采用了北京大学出版的《最优化：建模、算法与理论》这本书中的部分理论方法框架，运用了 Numpy 包高效处理数组间运算等的特性，巧妙地应用了 Sympy 内部支持的 .jacobian 等方法，并结合 Python 内置函数 dict 与 zip 实现了 Sympy 矩阵到 Numpy 矩阵的转换，最终设计了一个用于最优化科学研究领域的Python工具包。研究人员可以通过简单的 pip 指令进行下载与使用。项目内无约束优化与约束优化板块的算法仍然需要不断更新、维护与扩充，并且应用于混合约束优化板块的算法将在日后上线。我们非常欢迎广大热爱数学、编程的各界人士加入开发与更新最优化计算方法的队伍中，提出新的框架或算法，成为里程碑中的一员。

项目结构

|- optimtool
    |-- constrain
        |-- __init__.py
        |-- equal.py
        |-- mixequal.py
        |-- unequal.py
    |-- example
        |-- __init__.py
        |-- Lasso.py
        |-- WanYuan.py
    |-- functions
        |-- __init__.py
        |-- linear_search.py
        |-- tools.py
    |-- hybrid
        |-- __init__.py
        |-- approximate_point_gradient.py
    |-- unconstrain
        |-- __init__.py
        |-- gradient_descent.py
        |-- newton.py
        |-- newton_quasi.py
        |-- nonlinear_least_square.py
        |-- trust_region.py  
    |-- __init__.py

??因为在求解不同的目标函数的全局或局部收敛点时，不同的求取收敛点的方法会有不同的收敛效率以及不同的适用范围，而且在研究过程中不同领域的研究方法被不断地提出、修改、完善、扩充，所以这些方法成了现在人们口中的最优化方法。此项目中的所有内部支持的算法，都是在范数、导数、凸集、凸函数、共轭函数、次梯度和最优化理论等基础方法论的基础上进行设计与完善的。

??optimtool内置了诸如Barzilar Borwein非单调梯度下降法、修正牛顿法、有限内存BFGS方法、截断共轭梯度法-信赖域方法、高斯-牛顿法等无约束优化领域收敛效率与性质较好的算法，以及用于解决约束优化问题的二次罚函数法、增广拉格朗日法等算法。

Github源码：linjing-lab/optimtool

开始使用

无约束优化算法（unconstrain）

import optimtool.unconstrain as ou
ou.[方法名].[函数名]([目标函数], [参数表], [初始迭代点])

梯度下降法（gradient_descent）

ou.gradient_descent.[函数名]([目标函数], [参数表], [初始迭代点])

方法头	解释
solve(funcs, args, x_0, draw=True, output_f=False, epsilon=1e-10, k=0)	通过解方程的方式来求解精确步长
steepest(funcs, args, x_0, draw=True, output_f=False, method=“wolfe”, epsilon=1e-10, k=0)	使用线搜索方法求解非精确步长（默认使用wolfe线搜索）
barzilar_borwein(funcs, args, x_0, draw=True, output_f=False, method=“grippo”, M=20, c1=0.6, beta=0.6, alpha=1, epsilon=1e-10, k=0)	使用Grippo与Zhang hanger提出的非单调线搜索方法更新步长

牛顿法（newton)

ou.newton.[函数名]([目标函数], [参数表], [初始迭代点])

方法头	解释
classic(funcs, args, x_0, draw=True, output_f=False, epsilon=1e-10, k=0)	通过直接对目标函数二阶导矩阵（海瑟矩阵）进行求逆来获取下一步的步长
modified(funcs, args, x_0, draw=True, output_f=False, method=“wolfe”, m=20, epsilon=1e-10, k=0)	修正当前海瑟矩阵保证其正定性（目前只接入了一种修正方法）
CG(funcs, args, x_0, draw=True, output_f=False, method=“wolfe”, epsilon=1e-6, k=0)	采用牛顿-共轭梯度法求解梯度（非精确牛顿法的一种）

拟牛顿法（newton_quasi）

ou.newton_quasi.[函数名]([目标函数], [参数表], [初始迭代点])

方法头	解释
bfgs(funcs, args, x_0, draw=True, output_f=False, method=“wolfe”, m=20, epsilon=1e-10, k=0)	BFGS方法更新海瑟矩阵
dfp(funcs, args, x_0, draw=True, output_f=False, method=“wolfe”, m=20, epsilon=1e-4, k=0)	DFP方法更新海瑟矩阵
L_BFGS(funcs, args, x_0, draw=True, output_f=False, method=“wolfe”, m=6, epsilon=1e-10, k=0)	双循环方法更新BFGS海瑟矩阵

非线性最小二乘法（nonlinear_least_square）

ou.nonlinear_least_square.[函数名]([目标函数], [参数表], [初始迭代点])

方法头	解释
gauss_newton(funcr, args, x_0, draw=True, output_f=False, method=“wolfe”, epsilon=1e-10, k=0)	高斯-牛顿提出的方法框架，包括OR分解等操作
levenberg_marquardt(funcr, args, x_0, draw=True, output_f=False, m=100, lamk=1, eta=0.2, p1=0.4, p2=0.9, gamma1=0.7, gamma2=1.3, epsilon=1e-10, k=0)	Levenberg Marquardt提出的方法框架

信赖域方法（trust_region）

ou.trust_region.[函数名]([目标函数], [参数表], [初始迭代点])

方法头	解释
steihaug_CG(funcs, args, x_0, draw=True, output_f=False, m=100, r0=1, rmax=2, eta=0.2, p1=0.4, p2=0.6, gamma1=0.5, gamma2=1.5, epsilon=1e-6, k=0)	截断共轭梯度法在此方法中被用于搜索步长

约束优化算法（constrain）

import optimtool.constrain as oc
oc.[方法名].[函数名]([目标函数], [参数表], [等式约束表], [不等式约数表], [初始迭代点])

等式约束（equal）

oc.equal.[函数名]([目标函数], [参数表], [等式约束表], [初始迭代点])

方法头	解释
penalty_quadratic(funcs, args, cons, x_0, draw=True, output_f=False, method=“gradient_descent”, sigma=10, p=2, epsilon=1e-4, k=0)	增加二次罚项
lagrange_augmented(funcs, args, cons, x_0, draw=True, output_f=False, method=“gradient_descent”, lamk=6, sigma=10, p=2, etak=1e-4, epsilon=1e-6, k=0)	增广拉格朗日乘子法

不等式约束（unequal）

oc.unequal.[函数名]([目标函数], [参数表], [不等式约束表], [初始迭代点])

方法头	解释
penalty_quadratic(funcs, args, cons, x_0, draw=True, output_f=False, method=“gradient_descent”, sigma=10, p=0.4, epsilon=1e-10, k=0)	增加二次罚项
penalty_interior_fraction(funcs, args, cons, x_0, draw=True, output_f=False, method=“gradient_descent”, sigma=12, p=0.6, epsilon=1e-6, k=0)	增加分式函数罚项
penalty_interior_log(funcs, args, cons, x_0, draw=True, output_f=False, sigma=12, p=0.6, epsilon=1e-10, k=0)	增加近似点梯度法解决了迭代点溢出的问题
lagrange_augmented(funcs, args, cons, x_0, draw=True, output_f=False, method=“gradient_descent”, muk=10, sigma=8, alpha=0.2, beta=0.7, p=2, eta=1e-1, epsilon=1e-4, k=0)	增广拉格朗日乘子法

混合等式约束（mixequal）

oc.mixequal.[函数名]([目标函数], [参数表], [等式约束表], [不等式约束表], [初始迭代点])

方法头	解释
penalty_quadratic(funcs, args, cons_equal, cons_unequal, x_0, draw=True, output_f=False, method=“gradient_descent”, sigma=10, p=0.6, epsilon=1e-10, k=0)	增加二次罚项
penalty_L1(funcs, args, cons_equal, cons_unequal, x_0, draw=True, output_f=False, method=“gradient_descent”, sigma=1, p=0.6, epsilon=1e-10, k=0)	L1精确罚函数法
lagrange_augmented(funcs, args, cons_equal, cons_unequal, x_0, draw=True, output_f=False, method=“gradient_descent”, lamk=6, muk=10, sigma=8, alpha=0.5, beta=0.7, p=2, eta=1e-3, epsilon=1e-4, k=0)	增广拉格朗日乘子法

混合优化算法（hybrid）

import optimtool.hybrid as oh

近似点梯度下降法（approximate_point_gradient）

oh.approximate_point_gradient.[邻近算子名]([可微函数], [系数], [函数2], [参数表], [初始迭代点])

方法头	解释
L1(funcs, mu, gfun, args, x_0, draw=True, output_f=False, t=0.01, epsilon=1e-6, k=0)	L1范数邻近算子
neg_log(funcs, mu, gfun, args, x_0, draw=True, output_f=False, t=0.01, epsilon=1e-6, k=0)	负对数邻近算子

方法的应用（example）

import optimtool.example as oe

Lasso问题（Lasso）

oe.Lasso.[函数名]([矩阵A], [矩阵b], [因子mu], [参数表], [初始迭代点])

方法头	解释
gradient_descent(A, b, mu, args, x_0, draw=True, output_f=False, delta=10, alp=1e-3, epsilon=1e-2, k=0)	光滑化Lasso函数法
subgradient(A, b, mu, args, x_0, draw=True, output_f=False, alphak=2e-2, epsilon=1e-3, k=0)	次梯度法Lasso避免一阶不可导
penalty(A, b, mu, args, x_0, draw=True, output_f=False, gamma=0.1, epsilon=1e-6, k=0)	罚函数法
approximate_point_gradient(A, b, mu, args, x_0, draw=True, output_f=False, epsilon=1e-6, k=0)	邻近算子更新

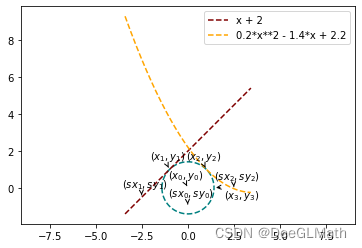
曲线相切问题（WanYuan）

oe.WanYuan.[函数名]([直线的斜率], [直线的截距], [二次项系数], [一次项系数], [常数项], [圆心横坐标], [圆心纵坐标], [初始迭代点])

问题描述：

给定直线的斜率和截距，给定一个抛物线函数的二次项系数，一次项系数与常数项。 要求解一个给定圆心的圆，该圆同时与抛物线、直线相切，若存在可行方案，请给出切点的坐标。

方法头	解释
gauss_newton(m, n, a, b, c, x3, y3, x_0, draw=False, eps=1e-10)	使用高斯-牛顿方法求解构造的7个残差函数

测试案例

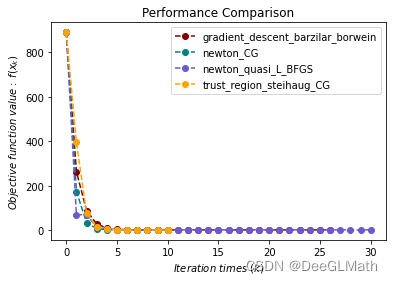
无约束优化问题测试

import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

f, x1, x2, x3, x4 = sp.symbols("f x1 x2 x3 x4")
f = (x1 - 1)**2 + (x2 - 1)**2 + (x3 - 1)**2 + (x1**2 + x2**2 + x3**2 + x4**2 - 0.25)**2
funcs = f # [f] \ (f) \ sp.Matrix([f])
args = [x1, x2, x3, x4] # (x1, x2, x3, x4) \ sp.Matrix([args])
x_0 = (1, 2, 3, 4)

f_list = []
title = ["gradient_descent_barzilar_borwein", "newton_CG", "newton_quasi_L_BFGS", "trust_region_steihaug_CG"]
colorlist = ["maroon", "teal", "slateblue", "orange"]
_, _, f = oo.unconstrain.gradient_descent.barzilar_borwein(funcs, args, x_0, False, True)
f_list.append(f)
_, _, f = oo.unconstrain.newton.CG(funcs, args, x_0, False, True)
f_list.append(f)
_, _, f = oo.unconstrain.newton_quasi.L_BFGS(funcs, args, x_0, False, True)
f_list.append(f)
_, _, f = oo.unconstrain.trust_region.steihaug_CG(funcs, args, x_0, False, True)
f_list.append(f)

# draw
handle = []
for j, z in zip(colorlist, f_list):
    ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
    handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()

非线性最小二乘问题测试

import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

r1, r2, x1, x2 = sp.symbols("r1 r2 x1 x2")
r1 = x1**3 - 2*x2**2 - 1
r2 = 2*x1 + x2 - 2
funcr = [r1, r2] # (r1, r2) \ sp.Matrix([funcr])
args = [x1, x2] # (x1, x2) \ sp.Matrix([args])
x_0 = (2, 2)

f_list = []
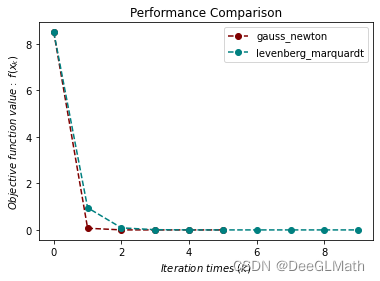
title = ["gauss_newton", "levenberg_marquardt"]
colorlist = ["maroon", "teal"]
_, _, f = oo.unconstrain.nonlinear_least_square.gauss_newton(funcr, args, x_0, False, True)
f_list.append(f)
_, _, f = oo.unconstrain.nonlinear_least_square.levenberg_marquardt(funcr, args, x_0, False, True)
f_list.append(f)

# draw
handle = []
for j, z in zip(colorlist, f_list):
    ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
    handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()

等式约束优化问题测试

import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

f, x1, x2 = sp.symbols("f x1 x2")
f = x1 + np.sqrt(3) * x2
c1 = x1**2 + x2**2 - 1
funcs = f # [f] \ (f) \ sp.Matrix([f])
cons = [c1] # c1 \ (c1) \ sp.Matrix([cons])
args = [x1, x2] # (x1, x2) \ sp.Matrix([args])
x_0 = (-1, -1)

f_list = []
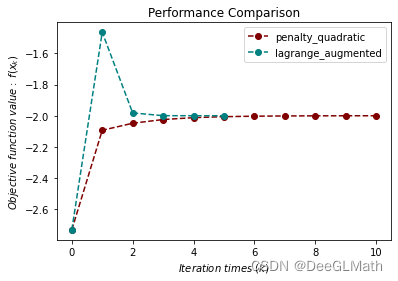
title = ["penalty_quadratic", "lagrange_augmented"]
colorlist = ["maroon", "teal"]
_, _, f = oo.constrain.equal.penalty_quadratic(funcs, args, cons, x_0, False, True)
f_list.append(f)
_, _, f = oo.constrain.equal.lagrange_augmented(funcs, args, cons, x_0, False, True)
f_list.append(f)

# draw
handle = []
for j, z in zip(colorlist, f_list):
    ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
    handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()

不等式约束优化问题测试

import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

f, x1, x2 = sp.symbols("f x1 x2")
f = x1**2 + (x2 - 2)**2
c1 = 1 - x1
c2 = 2 - x2
funcs = f # [f] \ (f) \ sp.Matrix([f])
cons = [c1, c2] # (c1, c2) \ sp.Matrix([cons])
args = [x1, x2] # (x1, x2) \ sp.Matrix([args])
x_0 = (2, 3)

f_list = []
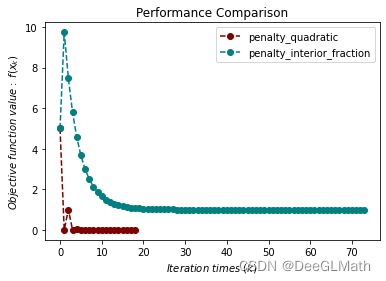
title = ["penalty_quadratic", "penalty_interior_fraction"]
colorlist = ["maroon", "teal"]
_, _, f = oo.constrain.unequal.penalty_quadratic(funcs, args, cons, x_0, False, True, method="newton", sigma=10, epsilon=1e-6)
f_list.append(f)
_, _, f = oo.constrain.unequal.penalty_interior_fraction(funcs, args, cons, x_0, False, True, method="newton")
f_list.append(f)

# draw
handle = []
for j, z in zip(colorlist, f_list):
    ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
    handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()

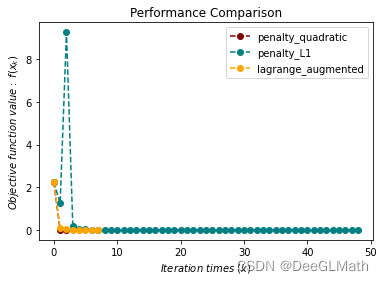
混合等式约束优化问题测试

import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

f, x1, x2 = sp.symbols("f x1 x2")
f = (x1 - 2)**2 + (x2 - 1)**2
c1 = x1 - 2*x2
c2 = 0.25*x1**2 - x2**2 - 1
funcs = f # [f] \ (f) \ sp.Matrix([f])
cons_equal = c1 # [c1] \ (c1) \ sp.Matrix([c1])
cons_unequal = c2 # [c2] \ (c2) \ sp.Matrix([c2])
args = [x1, x2] # (x1, x2) \ sp.Matrix([args])
x_0 = (0.5, 1)

f_list = []
title = ["penalty_quadratic", "penalty_L1", "lagrange_augmented"]
colorlist = ["maroon", "teal", "orange"]
_, _, f = oo.constrain.mixequal.penalty_quadratic(funcs, args, cons_equal, cons_unequal, x_0, False, True)
f_list.append(f)
_, _, f = oo.constrain.mixequal.penalty_L1(funcs, args, cons_equal, cons_unequal, x_0, False, True)
f_list.append(f)
_, _, f = oo.constrain.mixequal.lagrange_augmented(funcs, args, cons_equal, cons_unequal, x_0, False, True)
f_list.append(f)

# draw
handle = []
for j, z in zip(colorlist, f_list):
    ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
    handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()

Lasso问题测试

import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

import scipy.sparse as ss
f, A, b, mu = sp.symbols("f A b mu")
x = sp.symbols('x1:9')
m = 4
n = 8
u = (ss.rand(n, 1, 0.1)).toarray()
A = np.random.randn(m, n)
b = A.dot(u)
mu = 1e-2
args = x # list(x) \ sp.Matrix(x)
x_0 = tuple([1 for i in range(8)])

f_list = []
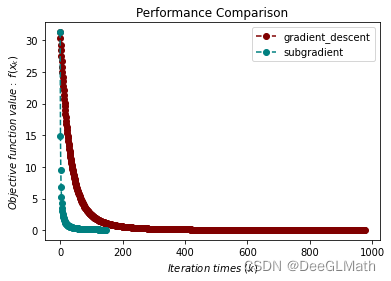
title = ["gradient_descent", "subgradient"]
colorlist = ["maroon", "teal"]
_, _, f = oo.example.Lasso.gradient_descent(A, b, mu, args, x_0, False, True, epsilon=1e-4)
f_list.append(f)
_, _, f = oo.example.Lasso.subgradient(A, b, mu, args, x_0, False, True)
f_list.append(f)

# draw
handle = []
for j, z in zip(colorlist, f_list):
    ln, = plt.plot([i for i in range(len(z))], z, c=j, marker='o', linestyle='dashed')
    handle.append(ln)
plt.xlabel("$Iteration \ times \ (k)$")
plt.ylabel("$Objective \ function \ value: \ f(x_k)$")
plt.legend(handle, title)
plt.title("Performance Comparison")
plt.show()

曲线切点问题测试

# import packages
import sympy as sp
import matplotlib.pyplot as plt
import optimtool as oo

# make data
m = 1
n = 2
a = 0.2
b = -1.4
c = 2.2
x3 = 2*(1/2)
y3 = 0
x_0 = (0, -1, -2.5, -0.5, 2.5, -0.05)

# train
oo.example.WanYuan.gauss_newton(1, 2, 0.2, -1.4, 2.2, 2**(1/2), 0, (0, -1, -2.5, -0.5, 2.5, -0.05), draw=True)