PID控制和阻抗控制在形式上是相似的,都是利用偏差,将偏差输入控制器,经过控制器的模型后产生输出。
PID控制和阻抗控制的根本不同是控制器模型的不同。模型的不同导致输出结果是不同的。
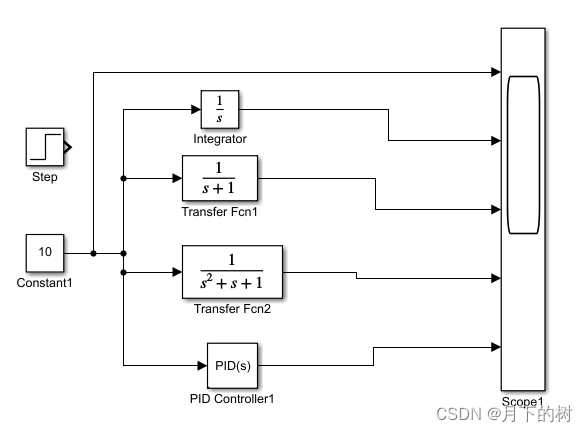
 PID的模型如下:
PID的模型如下:

PID的这个模型不能给予明确的物理解释,所以说PID的控制是没有道理的。
同时PID的作用是降低干扰尽快到达设定目标处,因为只知道尽快到达设定目标处,所以这种模型没有柔顺性,最典型的就是利用PID的位置控制
阻抗控制,天然和柔顺性结合在一起,说阻抗控制时都会把阻抗比喻成弹簧阻尼系统,阻抗模型中的系数代表着弹性和阻尼的大小。阻抗控制的形式是二阶系统,是可以和弹簧阻尼对应的二阶系统,也就是阻抗模型可以由物理意义解释
阻抗模型,PID模型和阻抗控制器、PID控制器是一回事,不作区分。阻抗控制器的模型、PID控制器的模型,和动力学没有关系,和动力学模型没有丝毫关系,这是两个完全不同的概念,PID控制器后也有可能接动力学模型。阻抗模型的二阶形式和动力学模型的二阶形式非常类似,以至于有时将阻抗模型和动力学模型混为一谈。在机器人阻抗控制中,的确有时会用到动力学模型,但是仍然要明确,阻抗模型和动力学模型没有关系,他们只是同时出现在了阻抗控制环路中,并且恰好形式一致
阻抗模型和动力学怎么关联,动力学模型和阻抗模型有个共同的力矩,通过这个力矩进行关联。
基于动力学前馈的阻抗控制,就是把阻抗控制和动力学组合到一块。
没有动力学照样可以做阻抗控制
基于位置的阻抗控制:
输入位置(理想位置和接触位置的差值)进入阻抗模型输出力,输出的力和理想力的差值通过力控制器控制机器人。这个力控制器可以是多种形式。
基于力的阻抗控制:
输入力(理想力和接触力的差值)进入阻抗模型输出位置,输出的位置和理想位置的差值通过位置控制器控制机器人。这个位置控制器可以是多种形式。
******************************分割线
阻抗控制目的:通过阻抗控制对机器人末端与环境之间的接触力进行调节,实现机器人末端与环境接触的柔顺性,保证接触作业的安全完成。
1.阻抗控制的作用
对于切削、磨光、装配等需要与外界环境接触的作业而言,仅有位置控制难以保证工作任务的安全完成。这是因为位置控制无法做到运动轨迹与期望轨迹的完美吻合,会存在一定的位置误差,这种误差可能会导致机器人末端与接触物体之间的接触力过大,严重的话会造成机器人或接触物体的损坏。
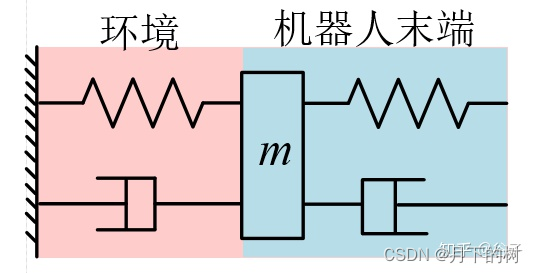
为了减缓位置偏差造成的过大接触力,直接的想法是我们可以在机器人末端加一个弹簧(K)。为了避免震荡可以再并联一个阻尼器(B)。惯性是物体(弹簧+阻尼器)的一种固有属性,质量(M)是对物体惯性大小的量度。这样机器人末端就相当于添加了一个质量-阻尼-弹簧系统。
阻抗控制其实就相当于在机器人末端添加的一个质量-阻尼-弹簧系统,建立末端位置与接触力的关系。根据机器人末端的位置和作用力之间的关系,通过调整位置误差来间接控制机器人末端的接触力。
- 阻抗控制公式

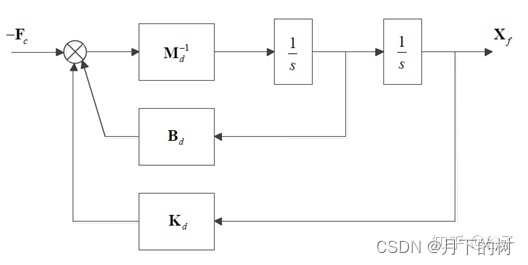
严格讲这个图配的是导纳的图
参考:基于阻抗控制的机器人力控制技术研究. 丁润泽. 哈尔滨工业大学
https://www.cnblogs.com/21207-iHome/p/12148726.html
动力学方程:
通常可将根据动量矩定理或牛顿-欧拉法推导出的等式写为如下形式:
τ=M(θ)θ¨+C(θ,θ˙)+G(θ)
如果机械臂自由度为n,M(θ)为n×n阶正定对称矩阵,M(θ)θ¨代表惯性力项。M(θ)中的主对角线元素表示各连杆本身的有效惯量,代表给定关节上的力矩与产生的角加速度之间的关系,非对角线元素表示连杆之间的耦合惯量,即是某连杆的加速运动对另一关节产生的耦合作用力矩的度量 ;C(θ,θ˙)为n×1阶向心力和科氏力项;G(θ)为n×1阶的重力项,与机器人的形位θ有关。
在纯位置控制下施加在机械臂末端的外力并不会影响末端的运动,因为这种情况可以认为机械臂是完全刚性的。而如果要实现主动柔顺控制,即使机械臂表现出一定的柔性就需要考虑其与环境之间的相互作用。这时关节驱动力矩可写为:
τ=M(θ)θ¨+C(θ,θ˙)+G(θ)+JT(θ)Ftip
上面等式中,Ftip为机械臂末端与外界环境之间的交互力,J为机械臂的雅可比矩阵,用于将关节空间速度映射到操作空间:v=Jθ˙,雅可比矩阵的转置也可将操作空间中的力映射到关节空间中:τ=JTF。对于本例,机器人雅可比矩阵可用MATLAB中的函数jacobian来计算,J=jacobian(rae,[θ1,θ2])。JT(θ)Ftip代表作用于机器人关节上的外界环境力矩,等式左边的τ为机器人关节驱动力矩,计算出该力矩后就可以输入给机器人驱动系统,实现期望的运动。
机械臂与环境交互产生的力矩可写为τext=JT(θ)Ftip=JT(θ)[M(xd¨?x¨)+D(xd˙?x˙)+K(xd?x)],xd和x分别代表目标位置和实际位置,xd˙和x˙分别代表目标速度和实际速度。注意这里的M D K和动力学中的M C G不是一回事,所以为了区分,用另外的字母表示:
τext=JT(θ)Ftip=JT(θ)[Md(xd¨?x¨)+Dd(xd˙?x˙)+Kd(xd?x)]
基于位置的阻抗控制
图1 这个图里面有理想接触力Fd(这个图其实有了动力学前馈)
这个图比较完整,里面体现了动力学
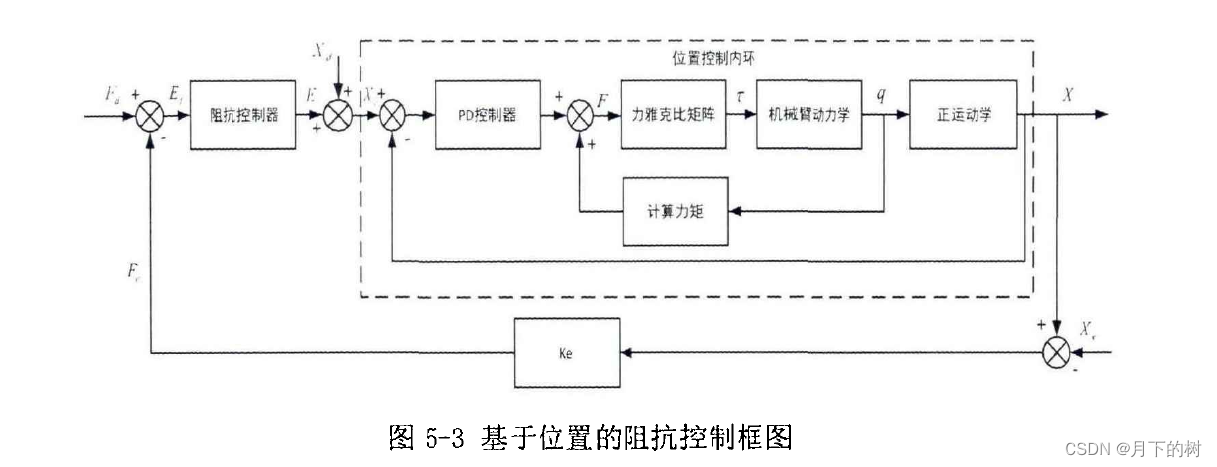
图2 这个图里面也有理想接触力Fr
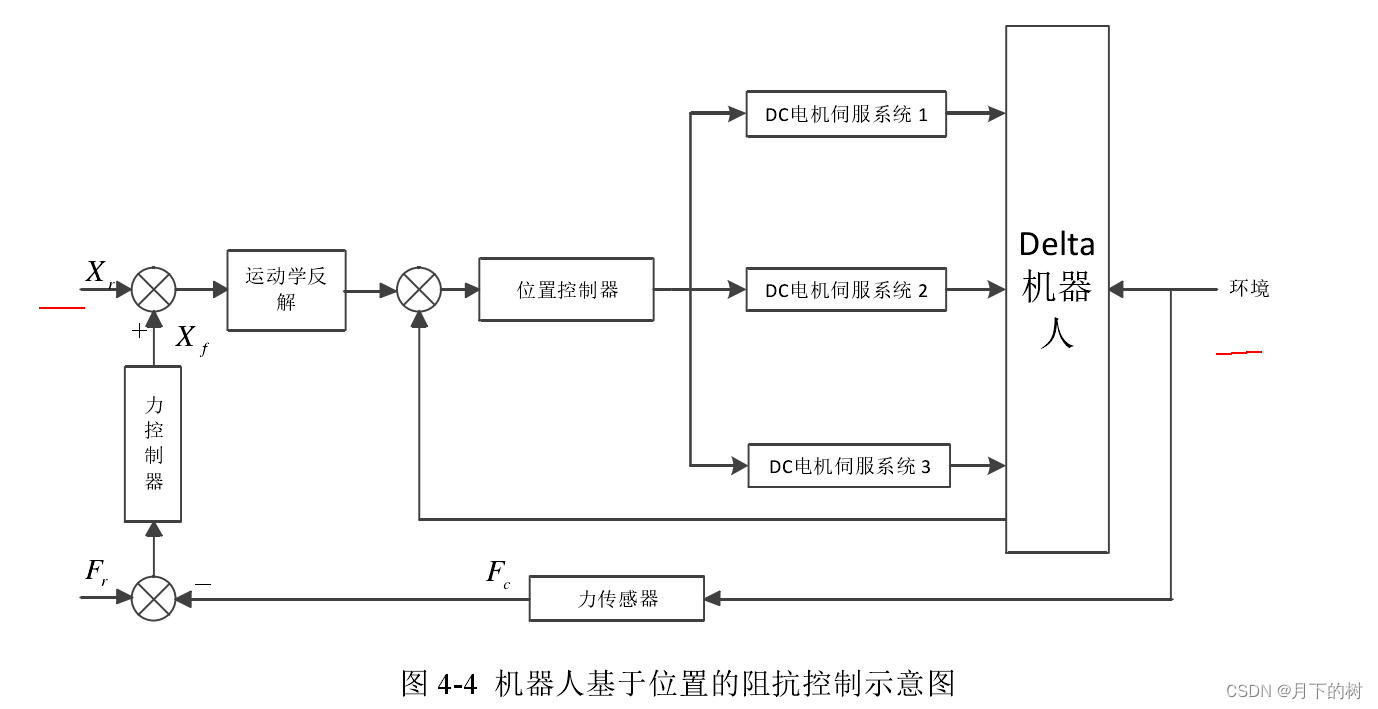
图3 这个图里面没有理想接触力 由位置偏差转化成了力Fe
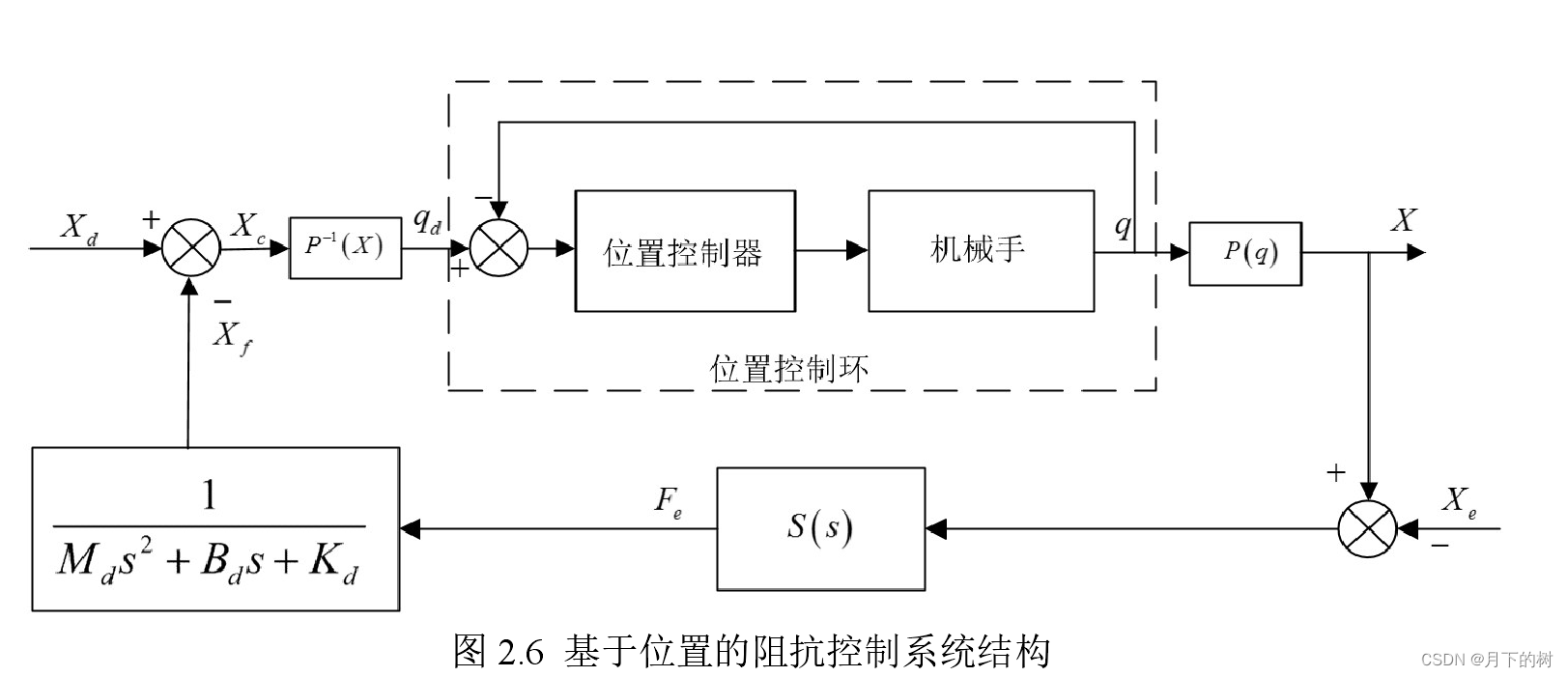
图4 自适应阻抗控制器(严格来说,图1-图4中的阻抗控制器都是导纳控制)
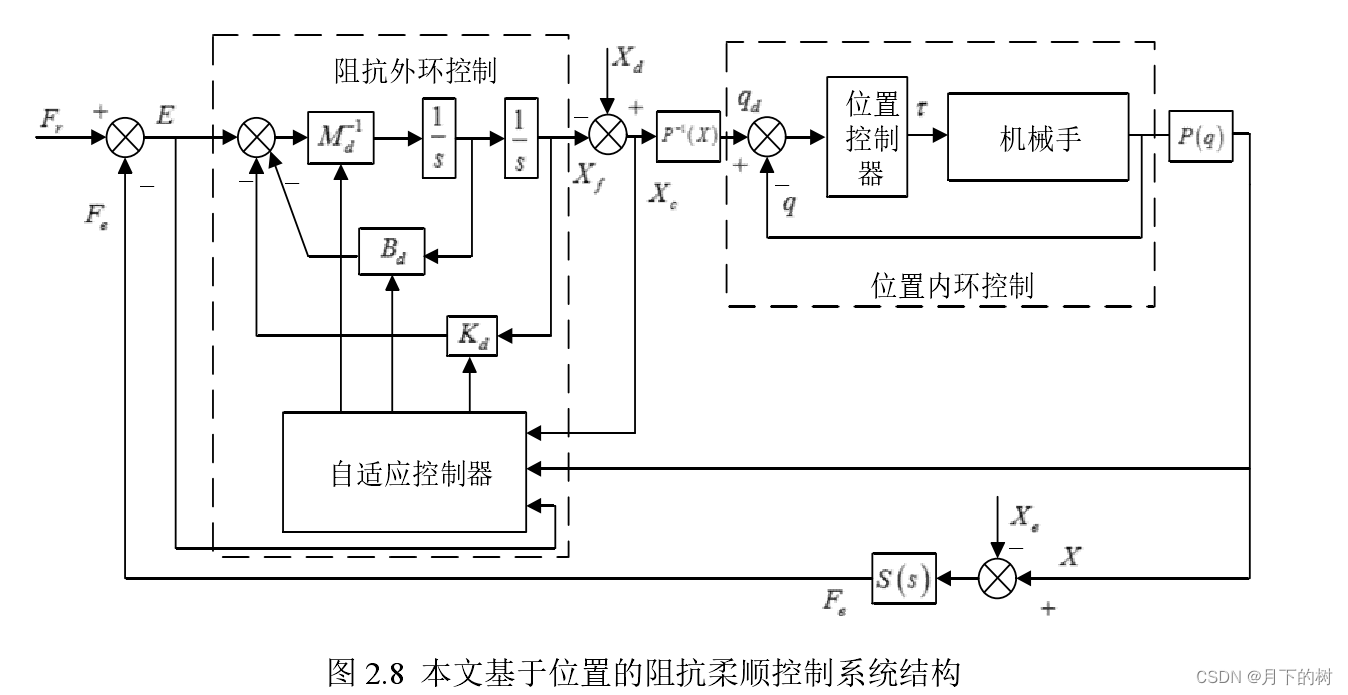
图5 动力学前馈
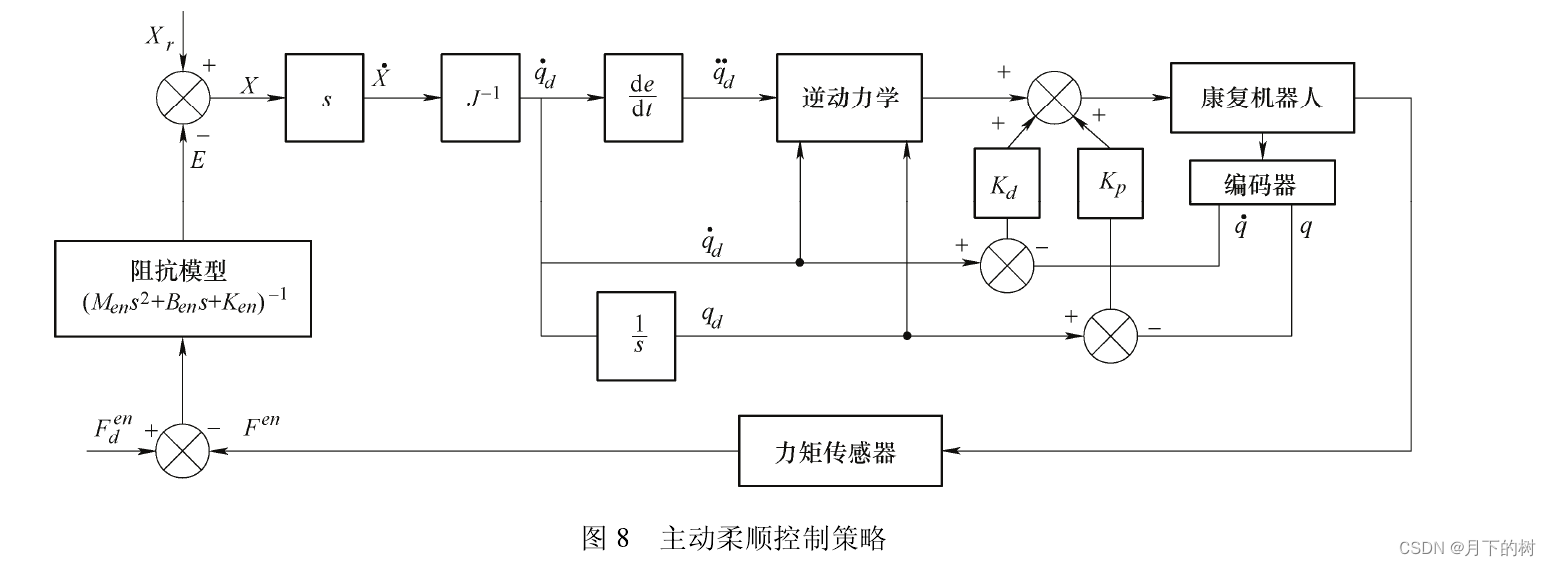
动力学前馈:
动力学方程:τ=M(θ)θ¨+C(θ,θ˙)+G(θ)
阻抗方程(环境接触力):Ftip =Md(xd¨?x¨)+Dd(xd˙?x˙)+Kd(xd?x)
动力学方程中考虑阻抗(基于动力学前馈的阻抗控制):
τ=M(θ)θ¨+C(θ,θ˙)+G(θ)+JT(θ)Ftip
基于动力学前馈的阻抗控制,就是把阻抗控制和动力学组合到一块。
没有动力学照样可以做阻抗控制
图6 基于力的阻抗控制系统
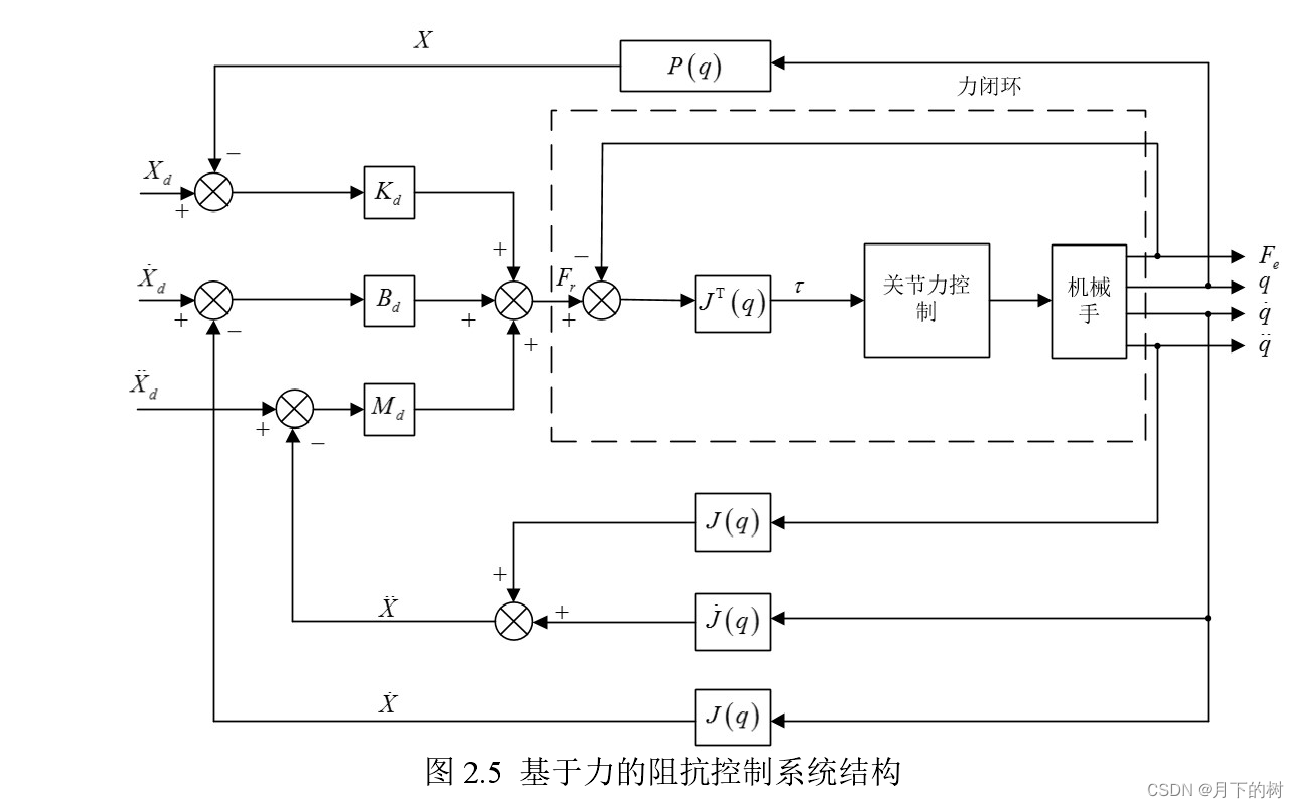
图6 没有用动力学,但是该模型是阻抗控制。
基于位置的阻抗控制:
输入位置(理想位置和接触位置的差值)进入阻抗模型输出力,输出的力和理想力的差值通过力控制器控制机器人。这个力控制器可以是多种形式。
基于力的阻抗控制:
输入力(理想力和接触力的差值)进入阻抗模型输出位置,输出的位置和理想位置的差值通过位置控制器控制机器人。这个位置控制器可以是多种形式。
阻抗和导纳可参考:
https://blog.csdn.net/xiaohejiaoyiya/article/details/105057619
https://zhuanlan.zhihu.com/p/165587437
从力到位置是导纳,从位置到力是阻抗