开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器学习中的几个重要概念 -> 正文阅读

[人工智能]机器学习中的几个重要概念

1.No free lunch theorem

机器学习中存在大量的各类不同模型，想要找到一个最好的模型适用不同的场合和不同的数据，这通常是不可能的，没有一个简单的所谓最好的模型能够适应不同的问题，这就是没有免费的午餐定理（No free lunch theorem）。原因在于不同的模型可能基于一定的假设（或称之inductive bias），而这些假设在特定的domain内表现的很好但在另一些domain可能表现很差。

2.Occam's Razor

? 奥卡姆剃刀（Occam's Razor）原理是指，在各种科学研究任务中，应该优先使用较为简单的公式或原理，而不是复杂的。应用到机器学习任务中，可以通过减小模型的复杂度来降低过拟合的风险，即模型在能够较好拟合训练集（经验风险）的前提下，尽量减小模型的复杂度（结构风险）。

3.BIC

在机器学习涉及多个模型的选取的问题（model selection）时，除了采用K折交叉验证外，一个更为有效的方法是计算模型的后验分布，具体如下

???????????????????????????????????????????????? $p(m|\mathcal D)=\frac{p( \mathcal D|m)p(m)}{\sum_{m\in \mathcal M}p(m,\mathcal D)}$

通过计算得到，? ? ? $\hat{m}=argmax\ p(m,\mathcal D)$ ,这就是所谓的Bayesian model selection。

如果选择模型的先验分布为均匀分布， $p(m) \propto 1$ ,上述 $p(m|\mathcal D)$ 的计算只与 $p(\mathcal D|m)$ 有关，这就等价于最大化

???????????????????????????????????????????????? $p(\mathcal D|m)=\int p(\mathcal D|\theta)p(\theta|m)d{\theta}$

上述结果称为边缘似然（marginal likelihood）或积分似然（integrated likelihood）或模型 $m$ ?的证据(evidence）。通常情况下计算上述边缘似然对应的积分表达式有点困难，一个通行的简化做法是计算Bayesian information criterion（BIC），

???????????????????????????????????????? $BIC \triangleq log \ p(\mathcal D|\hat{\theta})-\frac{dof(\hat{\theta})}{2}log {N} \approx log p(\mathcal D)$

如果定义模型的自由度?? $dof(\hat{\theta})=D$ ， $D$ ?是模型中变量的数量，就能得到：

????????????????????????????????????? ? ? ? ?? $BIC \triangleq log \ p(D)\approx log \ p(\mathcal D|\hat{\theta})-\frac{D}{2}log {N}$

BIC方法非常接近于最小描述长度MDL（minimum description length principle），也就是一个模型拟合数据的评分（log-likelihood）减去定义模型的复杂度,可以理解为带有惩罚项的log-likelihood。

4.AIC

与上述BIC/MDL非常相似的一个就是AIC信息准则（Akaike information criterion），定义如下

???????????????????????????????????????? $AIC(m,\mathcal D) \triangleq log\ p(\mathcal D|\hat{\theta}_{MLE})-dof(m)$

这个所谓的AIC源于频率派视觉得出，不同于贝叶斯派，所以上述不能理解为边缘似然的一个近似，然而这个表示形式与BIC非常相似。通过对比两者可知，AIC的惩罚项小于BIC，这使得AIC通常能选择更为复杂的模型，最终能够得到更好的预测准确性。

5.第一类最大似然

在统计与概率论中，估计统计模型参数的一个常用方法是使用MLE（Maximum likelihood estimation），具体定义如下

???????????????????????????????????????????????????????? $\hat{\theta} \triangleq \mathop{\arg\max}\limits_{\theta}log \ p(\mathcal D |\theta)$

上述MLE对应的似然通常称之为第一?类最大似然。

6.第二类最大似然

当使用Bayesian 方法时，为了评价边缘似然的效果，并不局限于采用网格法取有限值进行比较，而是采用数值优化方法，具体如下

???????????????????????????????????????????????????????????????? $\lambda ^ {*}=\mathop{\arg\max}\limits_{\lambda}p(D| \lambda)$

上述参数 $\lambda$ 是超参数，这种方法叫做经验贝叶斯方法或者第二类最大似然估计方法，与采用交叉验证评价不同超参数的模型，采用该方法更有效。

7.Simpson's paradox

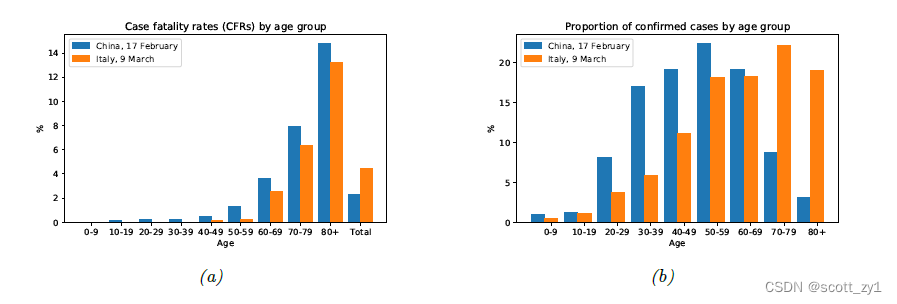
辛普森悖论（Simpson’s paradox）指的是统计上在各个分组中得到的趋势或结论，当各个分组合并到一起统计时得出的结论会出现刚好相反的结果，举例如下。在图a中统计对比中国和意大利各年龄段感染新冠病毒的致死率，各个年龄段的致死率中国都比意大利高，但是汇总的致死率却是意大利高于中国，原因在于意大利有更高的老龄化（老年人比例）。图a给出的是? $p(F=1|A,C)$ ,其中 $A,C$ 分别表示年龄和国家， $F$ ?表示感染新冠致死这一事件。图b给出的是? $p(A|C)$ ?表示在给定国家? $C$ ?时在人群在各个年龄组的概率，对比下图a,b主要的差异在于

???????????????? $p(F=1|A_i,C=China)>p(F=1|A_i,C=Italy),1\leq i(AgeIdx) \leq 9$

???????????????? $p(F=1|C=Italy)>p(F=1|C=China)$

8.Berkson's paradox

比如以预测下雨这一事件为例， $R=1,R=0$ 分别表示下雨和不下雨事件， $p(R=1)$ ?表示下雨的概率,根据先验知识满足? $p(R=1)=0.5$ ,?如果看到草地是湿的推测会下雨的概率达到了? $p(R=1|W=1)=0.7$ ，其中? $W=1$ ?表示草地湿的这一事件， $W=0$ 表示草地是干的，在此基础上如果看到了有洒水器 $S=1$ ?这一事件，此时推测下雨的概率为 $p(R=1|W=1,S=1)=0.3$ , 上述一些观察结果的多种原因之间的这种消极相互作用被称为解释效应，也被称为伯克森悖论。

9.black swan paradox

在bayes估计中为了避免zero-count的问题，通过平滑法 add-one smoothing ,比如投掷硬币试验只试验了一次，那么直接基于bayes估计得到头朝上的概率

??????????????????????????????????????????????????????????????? $\theta_{map}=\frac{N_1}{N_1+N_0}=0$ ，

采用 add-one smoothing(可以通过基于一个先验分布计算后验概率)，

?????????????????????????????????????????????????????????????????????? $\theta_{map}=\frac{N_1+1}{N_0+N_1+2}$

这也就是通过经验数据与先验知识来避免不可能存在的这种推测结果（黑天鹅悖论即不可能出现的情形）。

10.one-standard error rule

对于机器学习的训练任务，训练数据的经验风险 loss-function 定义如下

???????????????????????????????????????????????? $\mathcal L(\theta)=\frac{1}{N}\sum_{n=1}^{N}\mathit L(y_n,\theta;x_n)$

通过经验风险最小化来得到需要的模型。当训练样本有限时，通常使用交叉验证方法Cross-validation 训练数据集分为 K-folds 可以得到多个不同的模型对应有不同的超参数 $\lambda$ ，

???????????????????????????????????????? $R^{cv}_{\lambda}=\frac{1}{K}\sum_{k=1}^{K}R_0(\hat{\theta}_{\lambda(\mathcal D_{-k})},\mathcal D_k)$

其中 $\mathcal D_k$ 表示K-fold 数据集，? $\mathcal D_{-k}$ ???????表示K-fold 数据集外的其它数据?,那么，第n个样本集对应的loss

???????????????????????????????????????? $L_n=\mathit L(y_n,f(x_n;\hat{\theta}_{\lambda(\mathcal D_{-n})}))$

其中的超参数? $\lambda$ ?基于除了第 n 个样本集之外的数据训练得到。计算经验均值与经验方差如下

???????????????????????????????????????? $\hat{\mu}=\frac{1}{N}\sum_{n=1}^{N}L_n$

???????????????????????????????????????? $\hat{\sigma^2}=\frac{1}{N}\sum_{n=1}^{N}(L_n-\hat{\mu})^2$

假定我们应用交叉验证（cross validation）于一组模型，并计算其估计loss的平均值 $\hat{\mu}$ 与标准差 $\hat{\sigma}$ ，从这些带噪声估计值中选择模型的一种常见的启发式方法就是，选择与最佳模型的经验风险不超过一个标准误差的最简单模型；这被称为一个标准差准则（one-standard error rule），具体如下：