[人工智能]GrabCut分析

像素间相似性

中心像素和邻域像素的相似性有两个部分：位置相似和像素值相似

位置相似性：两个像素位置越接近，我们认为越相似。如以C为中心的邻域内，A和C的距离是$dis=\sqrt{2}$，B和C的距离是$dis=1$，相似性可以用$s_{pos}=\frac{1}{dis}$来衡量

$s_{pos}$值越大，越两个像素越相似

像素值相似：两个像素颜色越接近，我们认为越相似。如A和C的L2距离是$d_{L2}=|v(a)?v(b){|}^2$。这是一种简单的衡量方式，但它是值越小像素越相似，我们可以改进一下：

1、计算取反$?d_{L2}=?|v(a)?v(b){|}^2$，这样就变成了值越大越相似
2、再取指数$e^{?d_{L2}}$，这样变化范围就变成[0,1]区间了，但随之而来的问题是，随着变化量越大，计算结果差别会越小
3、再加一项调整指数范围$e^{?\beta \times d_{L2}}$，采用很小的β参数，可以解决2的问题

令像素相似性为$s_{pix}=e^{?\beta \times d_{L2}}$，值越大，越两个像素越相似

我们把两则综合一下，由于我们知道两者的范围其实差不多，所以直接相乘即可：

两个像素相似性计算公式：$s=s_{pos}\times s_{pix}$

图能量

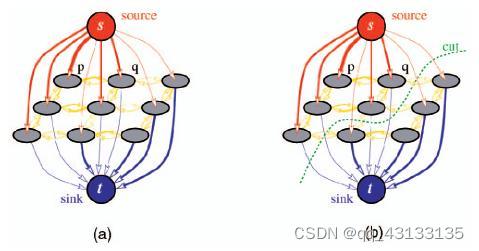
图中的边分为两类：n-links（黄色部分）和t-links（蓝色和橙色部分）。

n-links的n是neighbour的缩写，表示节点间的连接边，衡量节点不连续性（两节点差异越大，惩罚值越大）；

t-links的t是terminal的缩写，表示节点与终点（terminal）相连，衡量节点赋予所连接终点须耗费的代价值。

所以图的能量可以由n-links的惩罚值，和t-links的代价值描述：
$E=\sum V(p,q)+\sum D(p)$

最大流最小割

通过切断图的某些边，将图划分为S，T两个集合。并使得这些被切断的边的代价总和最小（即S,T集合的能量总和最大）。

也就是一个图的没分割之前，具有一定能量，我们要使得分割以后，两个图的能量之和最大

原理详细参考装逼之二 最小割与最大流（mincut & maxflow）
b站有个课程讲的很清晰，推荐观看：理解最大流最小割定理

grabcut源码分析

void cv_grabCut(InputArray _img, InputOutputArray _mask, Rect rect,
	InputOutputArray _bgdModel, InputOutputArray _fgdModel,
	int iterCount, int mode)
{
	Mat img = _img.getMat();
	Mat& mask = _mask.getMatRef();
	Mat& bgdModel = _bgdModel.getMatRef();
	Mat& fgdModel = _fgdModel.getMatRef();

	if (img.empty())
		CV_Error(CV_StsBadArg, "image is empty");
	if (img.type() != CV_8UC3)
		CV_Error(CV_StsBadArg, "image mush have CV_8UC3 type");

	GMM bgdGMM(bgdModel), fgdGMM(fgdModel);
	Mat compIdxs(img.size(), CV_32SC1);

	if (mode == GC_INIT_WITH_RECT || mode == GC_INIT_WITH_MASK)
	{
	    //初始化掩码窗口
		if (mode == GC_INIT_WITH_RECT)
		    //将窗口内所有mask像素都指明为可能是前景点，值为GC_PR_FGD
			initMaskWithRect(mask, img.size(), rect);
		else // flag == GC_INIT_WITH_MASK
		    //确保mask像素值取值是(GC_BGD , GC_FGD , GC_PR_BGD ,GC_PR_FGD)中的一个
			checkMask(img, mask);
		//将mask分为前景的背景两类，使用kmeans对每个类的数据聚类为componentsCount个标签
		//然后初始化前景和背景的GMM模型为componentsCount个分布，并利用之前的标签进行学习，得到GMM模型对应的参数
		initGMMs(img, mask, bgdGMM, fgdGMM);
	}

	if (iterCount <= 0)
		return;

	if (mode == GC_EVAL)
		checkMask(img, mask);

	const double gamma = 50;
	const double lambda = 9 * gamma;
	const double beta = calcBeta(img); //计算beta参数，用于n-link权重计算

	Mat leftW, upleftW, upW, uprightW;
	//计算像素每个像素8邻域的nlink权重，由于i->j的权重会再j->i里重复计算，所以只需要计算一半
	//  uL  u  uR
	//  L   p
	//
	calcNWeights(img, leftW, upleftW, upW, uprightW, beta, gamma);
	//进行迭代
	for (int i = 0; i < iterCount; i++)
	{
		GCGraph<double> graph;
		
		//高斯混合模型部分：
		
		//分别判断像素属于前景或者背景GMM模型的哪个分布，结果放在compIdxs
		assignGMMsComponents(img, mask, bgdGMM, fgdGMM, compIdxs);
		//将compIdxs的结果作为下一轮GMM学习的标签，对前景和背景GMM参数重新计算
		learnGMMs(img, mask, compIdxs, bgdGMM, fgdGMM);
		
		//图割部分：
		
		//每个像素作为一个图节点，初始化其n-link权重和t-link权重
		constructGCGraph(img, mask, bgdGMM, fgdGMM, lambda, leftW, upleftW, upW, uprightW, graph);
		//对图graph进行最大流最小割， 并对未指明的像素(GC_PR_BGD ， GC_PR_FGD)重新划分可能属于的类别
		estimateSegmentation(graph, mask);
	}
}