一、谱减法+维纳滤波+卡尔曼滤波语音去噪简介
1 维纳滤波算法
在传统的去噪算法中,维纳滤波因其操作简单、去噪效果好,被公认为一种经典的去噪算法。语音信号在时域的表示为: yi( t) = si( t) + ni( t) ,其中si( t) 、ni( t) 和yi( t) 分别是第i帧原始语音信号、噪声和被噪声污染的语音信号。维纳滤波原理是寻求一个线性滤波器H( n) ,使含噪语音yi( t) 经过线性滤波器后的估计值 ^si( t) = yi( t) * Hi( n) 与si( t) 之间的均方误差最小,进而从噪声ni( t) 干扰的含噪语音中分离出原纯净语音的理论。在si( t) 和ni( t) 都是平稳信号而且不相关的情况下,维纳滤波器在频域的最优估计函数为:
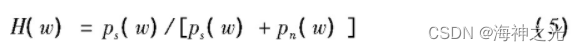
其中ps( w) 和pn( w) 分别是原始信号的功率谱和噪声的功率谱,则第i帧信号滤波后有用信号的谱估计为:

2 基本谱减法
S.Boll假设噪声信号是平稳的或变化缓慢的加性噪声,且在语音信号和噪声信号不相关的前提下提出谱减法,假定噪声是平稳的,人耳对相位信息不敏感,将含噪语音的相位作为处理后语音的相位,根据处理后的幅度和相位进行IFFT变换,得到增强后的时域信号。
设含噪语音为y (n),纯净语音为s (n),平稳加性高斯白噪声为d (n),有:
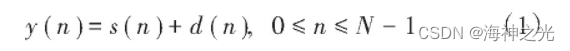
由傅里叶变换和纯净语音与含噪语音不相关,有:
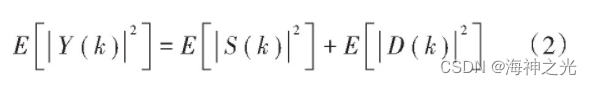
选取适当帧长语音信号为短时平稳过程后:
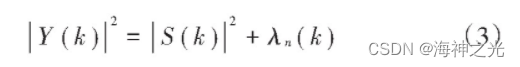
式中λn (k)为|D(k)|2的统计平均,这样就得到基本谱减法求出原始语音信号的估计值|S(k)|。
3 基于卡尔曼滤波的语音增强
现实中的噪声大都是非平稳的,因而研究非平稳噪声状态下的语音增强具有重要意义。
卡尔曼滤波在语音去噪已有许多研究应用,其结合语音生成模型,用信号的线性预测系数作为状态转移矩阵,增强后语音中残留的音乐噪声减少,语音自然度提高,其模型参数估计的准确与否直接影响增强语音的质量。卡尔曼滤波算法在语音信号去噪方面的应用研究较多,主要归功于其处理数据和计算算法实现等较为方便。
卡尔曼滤波器的主要过程有两个,分别是预估和校正。预估就是根据时间更新方程建立对当前状态的先验估计,方便构造下一状态的先验估计值;校正即是反馈过程,根据更新方程预估的先验估计值和当前测量值对现状态分析,改进后验估计值。
对含噪语音信号的计算式为:
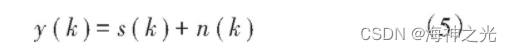
式中:s (k)为纯净语音;n (k)为与s (k)不相关的背景噪声。纯净语音s (k)在短时间段内认为是平稳的,其p阶AR预测方程为:
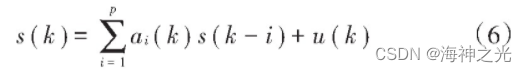
进一步得到系统的状态空间方程为:
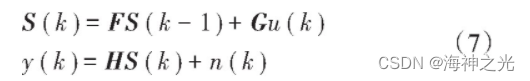
式中:S (k)是k时刻的系统状态,即语音实际值;F是LPC系数构成的状态转移矩阵;y (k)是k时刻的测量值;n (k)和u (k)分别为测量噪声和过程噪声,均值始终为零,且其方差分别为δn2和δu2的不相关白噪声;H和G分别为观测向量和输入向量。
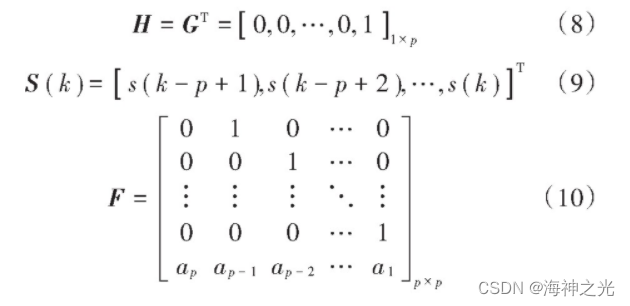
分帧后的语音信号在假设初始条件值后,通过卡尔曼滤波递推求出相应的结果:
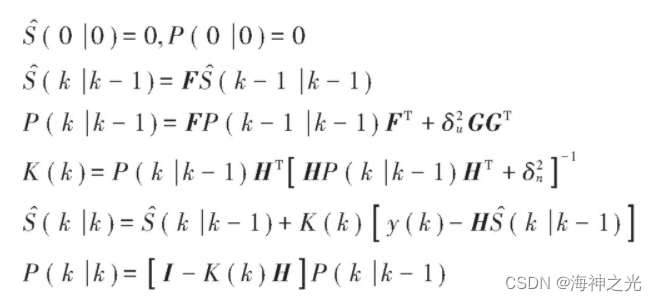
迭代计算后最终得出增强后的语音信号在k时刻的最佳估值:
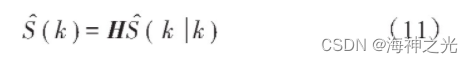
二、部分源代码
%%三种语音增强方法的测试脚本
%******************************************************
% 在audioread函数中可以设置读入的语音信号
% 改变SNR的值即可改变加入的噪声
%
[Input, Fs] = audioread('sp01.wav');
Time = (0:1/Fs:(length(Input)-1)/Fs)';
%取单声道
Input = Input(:,1);
%SNR为加入噪声与纯净信号的信噪比(dB)
SNR=10;
[NoisyInput,Noise] = add_noise(Input,SNR);%NoisyInput为加噪信号,Noise是噪声
%% 三种语音增强方法的实现
[spectruesub_enspeech] = spectruesub(NoisyInput);
[wiener_enspeech] = wienerfilter(NoisyInput);
[Klaman_Output] = kalman(NoisyInput,Fs,Noise);
%% spectruesub绘制
%将信号长度对齐
sig_len=length(spectruesub_enspeech);
NoisyInput=NoisyInput(1:sig_len);
Input=Input(1:sig_len);
wiener_enspeech=wiener_enspeech(1:sig_len);
Klaman_Output=Klaman_Output(1:sig_len);
Time = (0:1/Fs:(sig_len-1)/Fs)';
% Time= ((0:1/Fs:(sig_len)-1)/Fs)';
figure(1)
MAX_Am(1)=max(Input);
MAX_Am(2)=max(NoisyInput);
MAX_Am(3)=max(spectruesub_enspeech);
subplot(3,1,1);
plot(Time, Input)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('原始信号')
subplot(3,1,2);
plot(Time, NoisyInput)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('加噪信号')
subplot(3,1,3);
plot(Time, spectruesub_enspeech)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('谱减法')
%% spectruesub绘制
% Time_wiener = (0:1/Fs:(length(wiener_enspeech)-1)/Fs)';
figure(2)
MAX_Am(1)=max(Input);
MAX_Am(2)=max(NoisyInput);
MAX_Am(3)=max(wiener_enspeech);
subplot(3,1,1);
plot(Time, Input)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('原始信号')
subplot(3,1,2);
plot(Time, NoisyInput)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('加噪信号')
subplot(3,1,3);
plot(Time, wiener_enspeech)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('维纳滤波法')
%% Kalman绘制
figure(3)
MAX_Am(1)=max(Input);
MAX_Am(2)=max(NoisyInput);
MAX_Am(3)=max(Klaman_Output);
subplot(3,1,1);
plot(Time, Input)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('原始信号')
subplot(3,1,2);
plot(Time, NoisyInput)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('加噪信号')
subplot(3,1,3);
plot(Time, Klaman_Output)
ylim([-max(MAX_Am),max(MAX_Am)]);
xlabel('Time')
ylabel('Amlitude')
title('Kalman滤波')
%% 求语音降噪后的信噪比
SNR(1)=snr(Input,Input-spectruesub_enspeech);
SNR(2)=snr(Input,Input-wiener_enspeech);
SNR(3)=snr(Input,Input-Klaman_Output);
三、运行结果



四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]韩纪庆,张磊,郑铁然.语音信号处理(第3版)[M].清华大学出版社,2019.
[2]郑展恒,曾庆宁.语音增强算法的研究与改进[J].现代电子技术. 2020,43(21)
[3]靳立燕,陈莉,樊泰亭,高晶.基于奇异谱分析和维纳滤波的语音去噪算法[J].计算机应用. 2015,35(08)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除