[人工智能]【数据聚类】第三章第一节：基于划分的聚类算法概述

一：基于划分的聚类算法思想

基于划分的聚类算法：对于一个包含了$n$个样本的原始数据集，采用某种方法将其划分为$k$个划分（$k<n$），其中的每个划分均表示一个簇

• 基于划分的方法通过一个最优化的目标函数发掘数据中包含的类别信息结构，通过以迭代的方式逐步提高聚类结果
• 基于划分的方法又称为基于原型的方法（所谓原型，是指原型点，即可以体现出某一类别特性的代表的点）

在构建划分的过程中，需要注意

• 每个簇至少需要包含一个样本
• 每个样本都必须要有其所属的簇（且所属是唯一的）；随着模糊算法的发展，这一点其实已经被适当放宽

另外，在划分时，首先需要创建一个初始的划分（可以随机构建）。划分的究竟好不好，可以依据这一条准则判断：处于同一划分中的样本之间的差异要尽可能小，处在不同划分中的样本之间差异尽可能大

二：基于划分的聚类算法流程

算法描述

算法流程

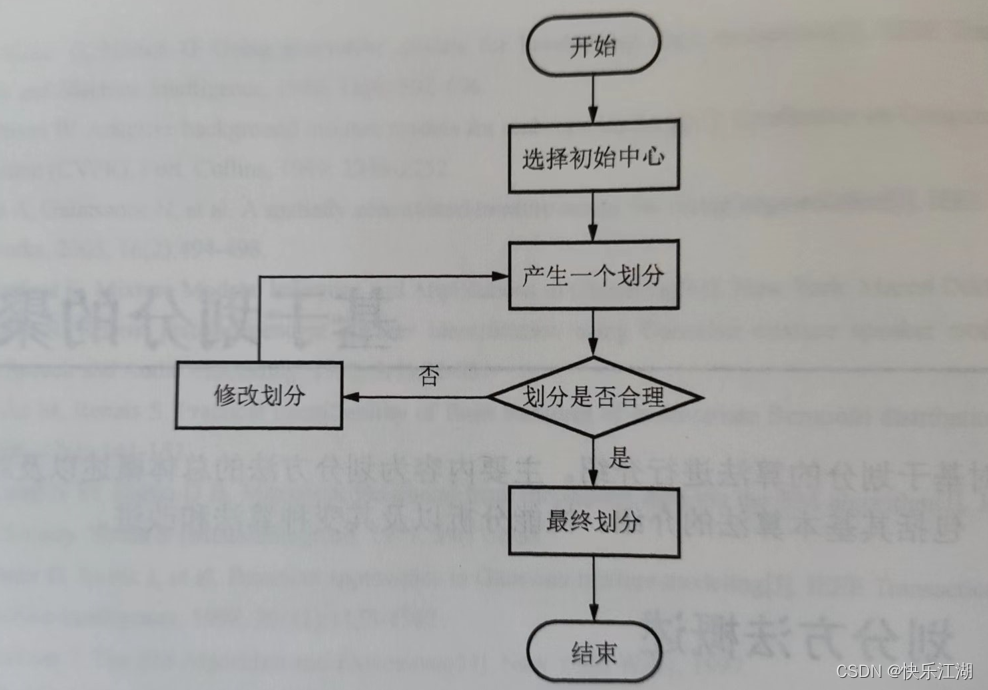
三：基于划分的聚类算法缺点

可以看出，基于划分的方法思想简单、实现方便，但不足之处在于

• 在划分的初始阶段，初始聚类的个数需要用户去设定；但在实际问题中，不同的人对同一个数据集往往有不同的看法，需要很强专业知识和经验，才能做出相对准确的判断
• 初始值的设定对聚类结果会造成很大影响；一般来说，如果初始值设置的小，那么就难以区分出某些存在差异的数据点，如果初始值设置大，那么本应该属于同一类别的数据点就会被错误的分配到不同类别中
• 划分方法只适用于部分类型的数据结构，当数据分布的形状不是基于中心的类型时（即非凸数据），聚类效果就会很差

四：基于划分的聚类算法有哪些

基于划分的聚类算法有很多种，算法的思想基本一致，主要区别有以下两点

• 如何产生一个对应划分方法上的选取
• 验证这种划分是否合理的一个判断标准的制定

在众多算法中，最出名、使用最频繁、综合性最高的当属 $k$-均值算法（$k?means$）

• 后续文章将会对$k$-均值算法的目标函数、贪心算法、性能分析、初始化策略、算法改进和变种、运行速度等方面进行详细介绍