[人工智能] 唤醒手腕 - 机器学习 - 人工神经网络（Artificial Neural Network）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 唤醒手腕 - 机器学习 - 人工神经网络（Artificial Neural Network） -> 正文阅读

[人工智能]唤醒手腕 - 机器学习 - 人工神经网络（Artificial Neural Network）

人工神经网络基本介绍

神经网络是一门重要的机器学习技术。它是目前最为火热的研究方向–深度学习的基础。学习神经网络不仅可以让你掌握一门强大的机器学习方法，同时也可以更好地帮助你理解深度学习技术。

人工神经网络（Artificial Neural Network），是一种模仿生物神经网络的结构和功能的数学模型或计算模型。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。

在这里插入图片描述

现代神经网络是一种非线性统计性数据建模工具，常用来对输入和输出间复杂的关系进行建模，或用来探索数据的模式。

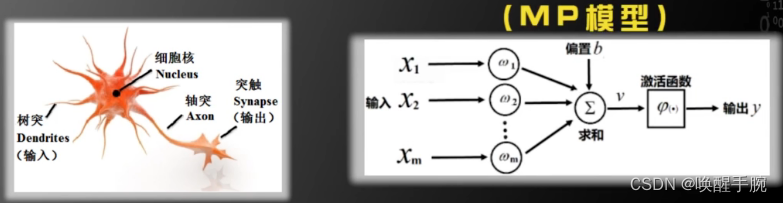
在这里插入图片描述
神经元模型是一个包含输入，输出与计算功能的模型。输入可以类比为神经元的树突，而输出可以类比为神经元的轴突，计算则可以类比为细胞核。

M - P Model 模型

所谓 M-P 模型，其实是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型。

大家可以查一查一些生物方面的书籍，了解一下这个神经元是如何工作的。我们可以概括出生物神经网络的假定特点：

每个神经元都是一个多输入单输出的信息处理单元；
神经元输入分兴奋性输入和抑制性输入两种类型；
神经元具有空间整合特性和阈值特性；
神经元输入与输出间有固定的时滞，主要取决于突触延搁

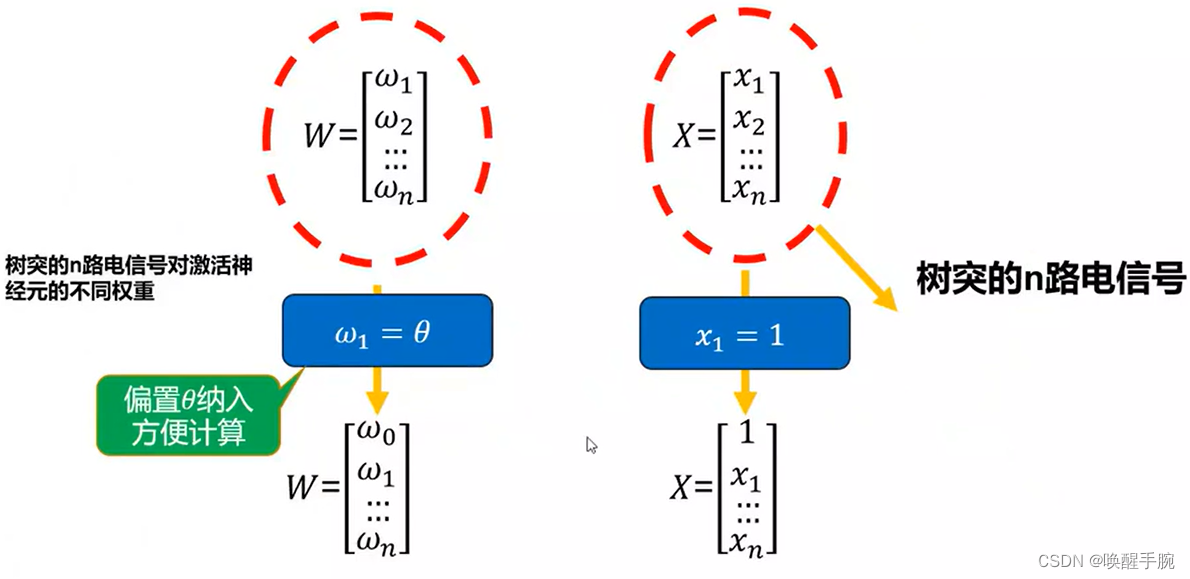
按照生物神经元，我们建立M-P模型。为了使得建模更加简单，以便于进行形式化表达，我们忽略时间整合作用、不应期等复杂因素，并把神经元的突触时延和强度当成常数。下图就是一个M-P模型的示意图。

在这里插入图片描述
由此我们可以得到总结出 M - P 模型的 6 个特点：

每个神经元都是一个多输入单输出的信息处理单元；
神经元输入分兴奋性输入和抑制性输入两种类型；
神经元具有空间整合特性和阈值特性；
神经元输入与输出间有固定的时滞，主要取决于突触延搁；
忽略时间整合作用和不应期；
神经元本身是非时变的，即其突触时延和突触强度均为常数。

在这里插入图片描述

神经元在逻辑电路的运用案例：
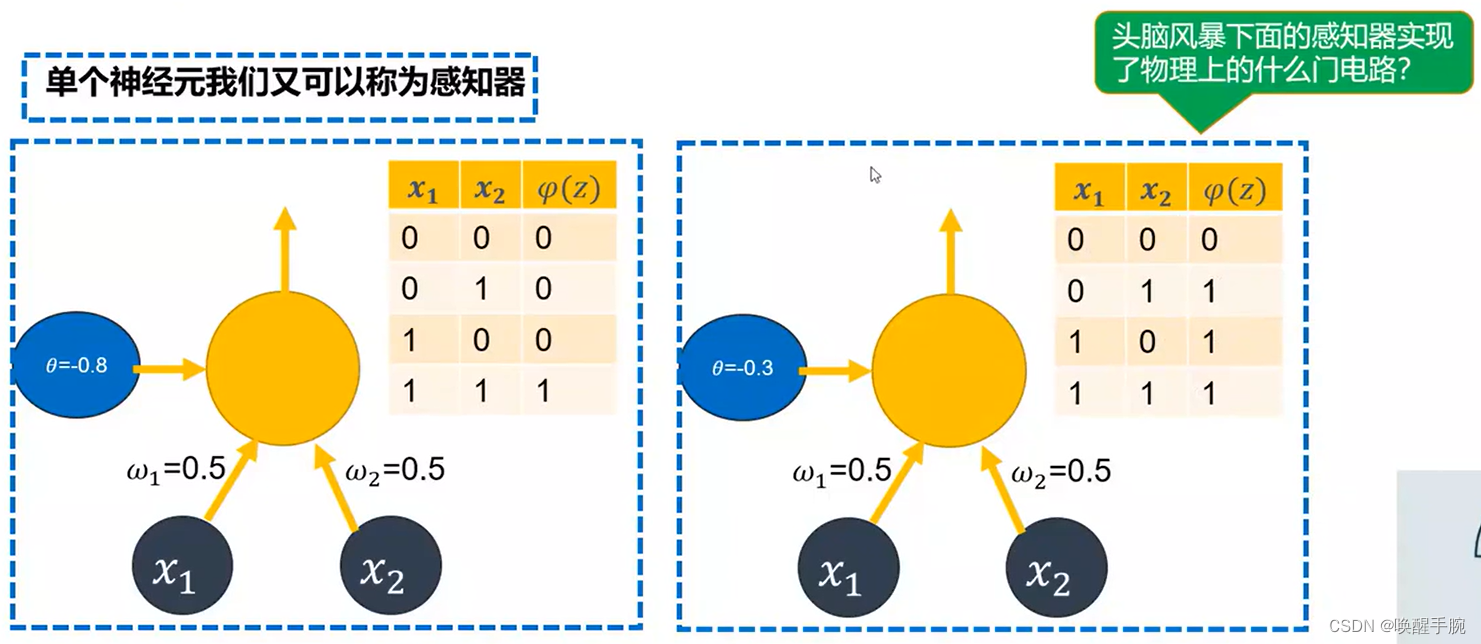
在这里插入图片描述

感知器算法原理介绍

感知器是人工神经网络中的一种典型结构，它的主要的特点是结构简单。它是一种分类学习器，是很多复杂算法的基础。其“赏罚概念”在机器学习算法在中广为应用。在分类正确时，对正确的权重向量w赏，即w不变；当分类错误时，对权重向量罚，即将权重向量w向着争取的方向转变。

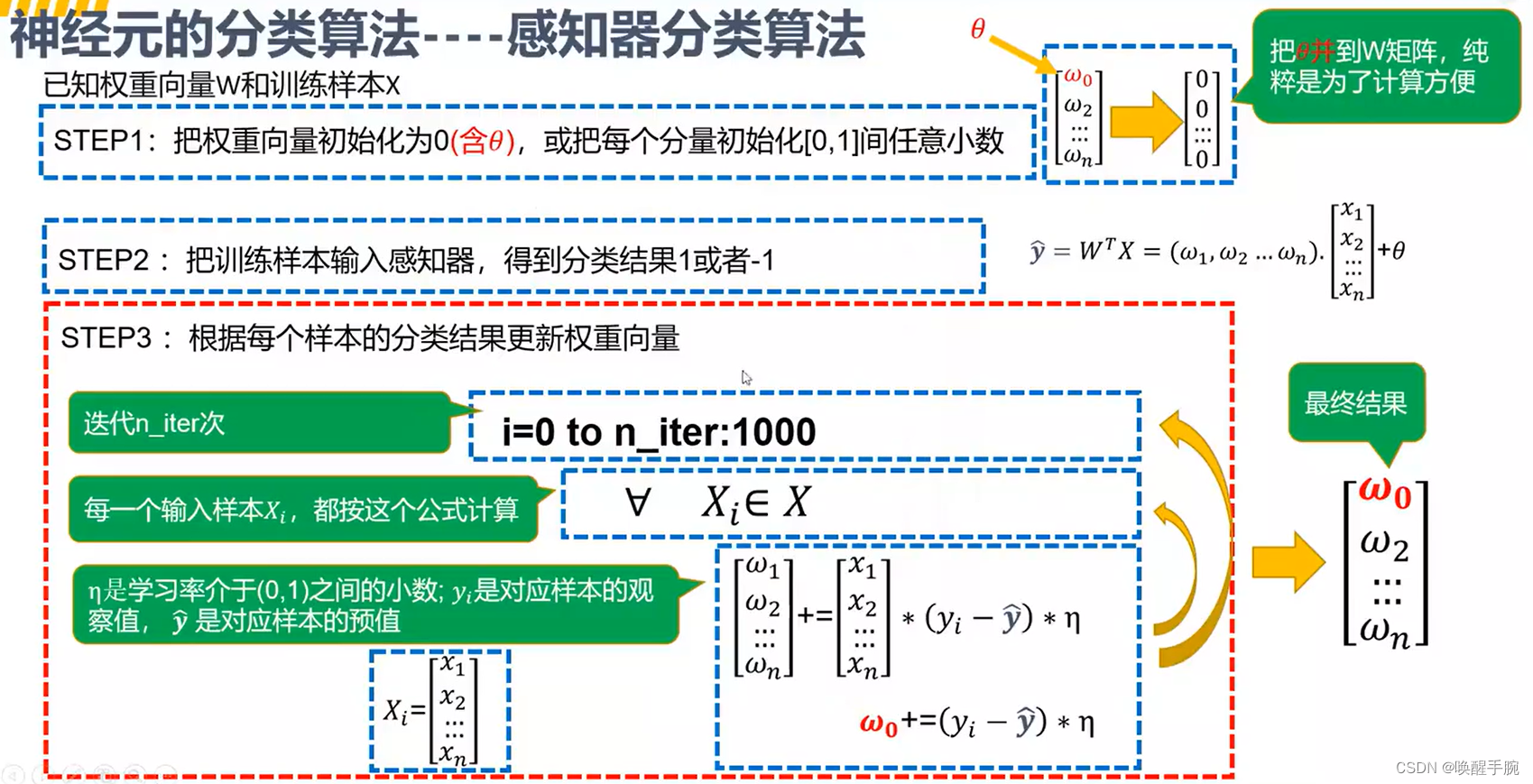
在这里插入图片描述

感知器算法的主要流程

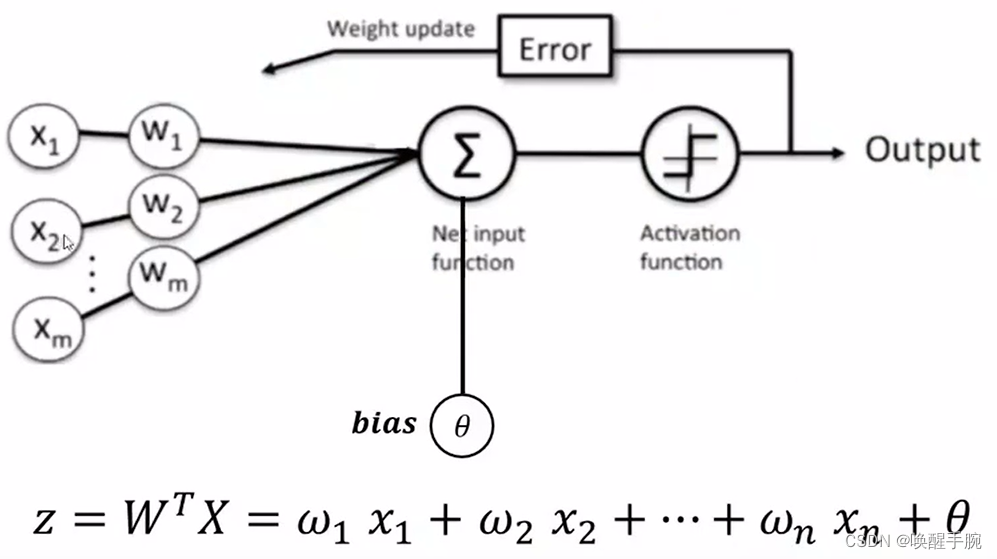
首先得到 n 个输入，再将每个输入值加权，然后判断感知器输入的加权和最否达到某一阀值 v，若达到，则通过 sign 函数输出 1，否则输出 -1，展示如下：

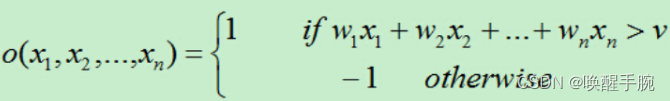
在这里插入图片描述
为了统一表达式，我们将上面的阀值 v 设为 0，新增变量 $x_0 =1$ ，这样就可以使用 $w_0x_0+w_1x_1+w_2x_2+…+w_nx_n$ ，于是有：

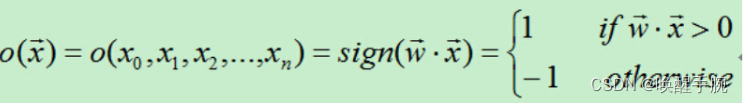
在这里插入图片描述

从上面的公式可知，当权值向量确定时，就可以利用感知器来做分类。那么我们如何获得感知器的权值呢？这需要根据训练集是否可分来采用不同的方法：

训练集线性可分时 > 感知器训练法则

为了得到可接受的权值，通常从随机的权值开始，然后利用训练集反复训练权值，最后得到能够正确分类所有样例的权向量。

通过逐步调整 w 的值，最终感知器将会收敛到能够将所有训练集正确分类的程度，但前提条件是训练集线性可分。若训练集线性不可分，则上述过程不会收敛，将无限循环下去。

简单神经网络实现

from numpy import array, exp, random, dot

X = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
Y = array([[0, 1, 1, 0]]).T  # The transposed array
random.seed(1)  # set random seed
weights = array([[0, 0, 0]]).T
for i in range(10000):
    output = 1/(1+exp(-dot(X, weights)))
    error = Y - output
    delta = error * output * (1 - output)
    weights = dot(X.T, delta) + weights

print(weights)

Python 实现感知器算法

生成线性可分的数据

import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()

x = iris.data
y = iris.target
# 只做一个简单的二分类
x = x[y < 2, :2]
y = y[y < 2]

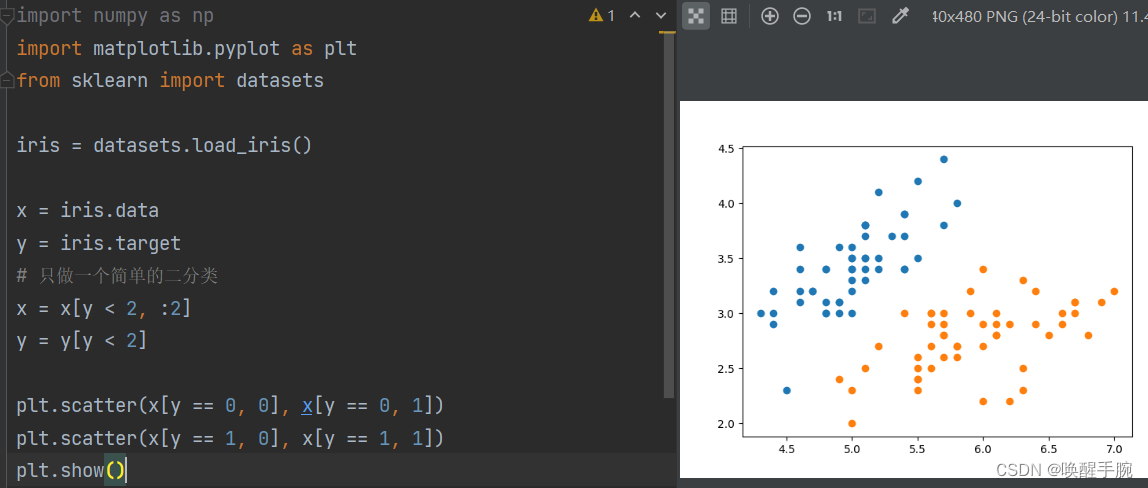
plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()

生成线性可分的数据运行结果展示：

在这里插入图片描述

实现算法展示：

def check(w, x, y):
    return ((w.dot(x.T) > 0).astype(int) == y).all()


def train(w, train_x, train_y, learn=1, max_iter=200):
    iter = 0
    while ~check(w, train_x, train_y) and iter <= max_iter:
        iter += 1
        for i in range(train_y.size):
            predict_y = (w.dot(train_x[i].T) > 0).astype(int)
            if predict_y != train_y[i]:
                w += learn * (train_y[i] - predict_y) * train_x[i]
    return w


def normalize(x):
    max_x = np.max(x, axis=0)
    min_x = np.min(x, axis=0)
    norm_x = (max_x - x) / (max_x - min_x)
    return norm_x


norm_x = normalize(x)
train_x = np.insert(norm_x, 0, values=np.ones(100).T, axis=1)
w = np.random.random(3)
w = train(w, train_x, y)

绘制决策边界展示：

def plot_decision_boundary(w, axis):
    x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(1, -1),
                         np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(1, -1), )
    x_new = np.c_[x0.ravel(), x1.ravel()]
    x_new = np.insert(x_new, 0, np.ones(x_new.shape[0]), axis=1)
    y_predict = (w.dot(x_new.T) > 0).astype(int)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])

    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)


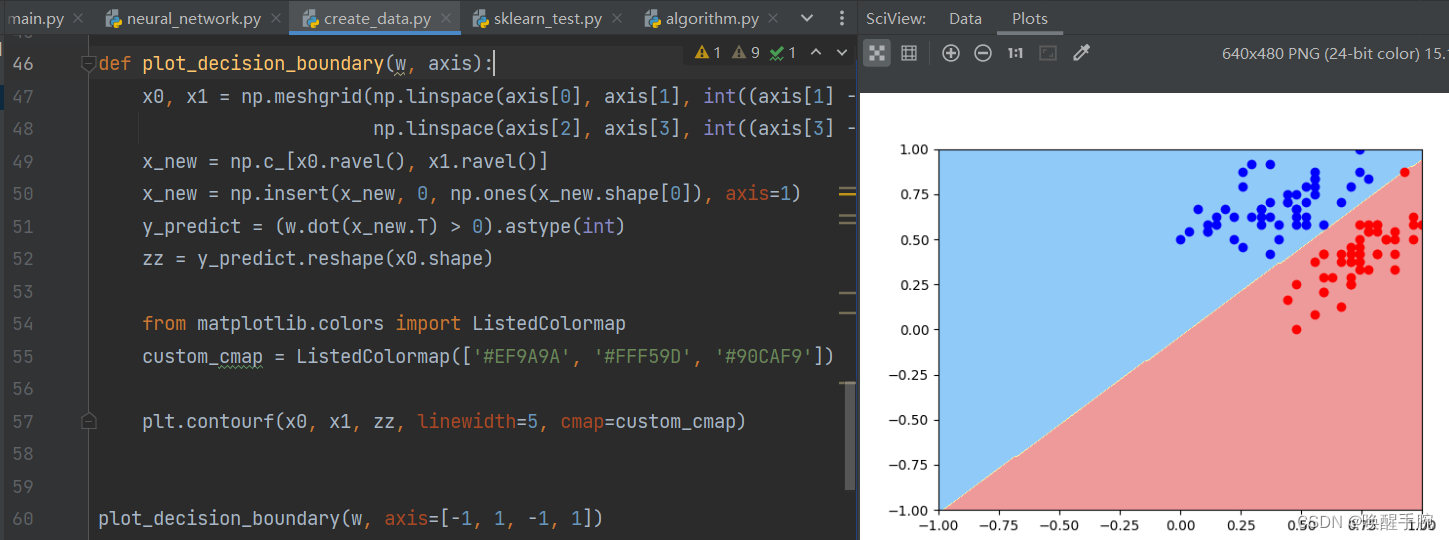
plot_decision_boundary(w, axis=[-1, 1, -1, 1])
plt.scatter(norm_x[y == 0, 0], norm_x[y == 0, 1], color='red')
plt.scatter(norm_x[y == 1, 0], norm_x[y == 1, 1], color='blue')
plt.show()

绘制决策边界展示运行结果展示：

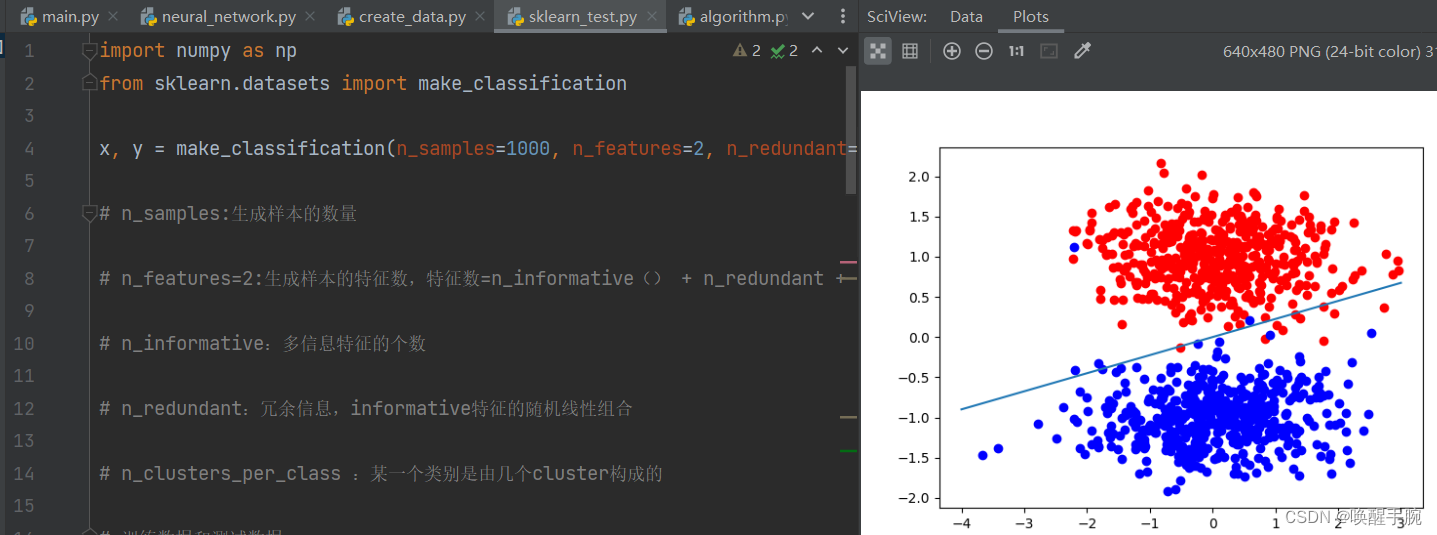
在这里插入图片描述

使用 sklearn 包完成感知器算法

import numpy as np
from sklearn.datasets import make_classification

x, y = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=1, n_clusters_per_class=1)

# n_samples:生成样本的数量

# n_features=2:生成样本的特征数，特征数=n_informative（） + n_redundant + n_repeated

# n_informative：多信息特征的个数

# n_redundant：冗余信息，informative特征的随机线性组合

# n_clusters_per_class ：某一个类别是由几个cluster构成的

# 训练数据和测试数据
x_data_train = x[:800, :]
x_data_test = x[800:, :]
y_data_train = y[:800]
y_data_test = y[800:]

# 正例和反例
positive_x1 = [x[i, 0] for i in range(1000) if y[i] == 1]
positive_x2 = [x[i, 1] for i in range(1000) if y[i] == 1]
negetive_x1 = [x[i, 0] for i in range(1000) if y[i] == 0]
negetive_x2 = [x[i, 1] for i in range(1000) if y[i] == 0]
from sklearn.linear_model import Perceptron

# 定义感知机
clf = Perceptron(fit_intercept=False, shuffle=False)
# 使用训练数据进行训练
clf.fit(x_data_train, y_data_train)
# 得到训练结果，权重矩阵
print(clf.coef_)
# 输出为：[[-0.38478876,4.41537463]]

# 超平面的截距，此处输出为：[0.]
print(clf.intercept_)

# 利用测试数据进行验证
acc = clf.score(x_data_test, y_data_test)
print(acc)
# 得到的输出结果为0.98，这个结果还不错吧。
from matplotlib import pyplot as plt

# 画出正例和反例的散点图
plt.scatter(positive_x1, positive_x2, c='red')
plt.scatter(negetive_x1, negetive_x2, c='blue')
# 画出超平面（在本例中即是一条直线）
line_x = np.arange(-4, 4)
line_y = line_x * (-clf.coef_[0][0] / clf.coef_[0][1]) - clf.intercept_
plt.plot(line_x, line_y)
plt.show()