一、numpy概述
- numpy用于快速处理任意维度的数组,主要来说就是对矩阵操作。
- numpy是使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
- ndarray是一个n维数组类型
Python列表可以实现多维数组,那么为什么还需要ndarray呢?
numpy专门针对ndarray的操作和运算进行了设计,所以该类型的存储效率和输入输出性能远优于Python中的嵌套列表,数组越大,Numpy的优势就越明显。
二、ndarray基本操作
1、ndarray的属性
| 属性名 | 解释 |
|---|---|
| ndarray.shape | 数组维度的元组 |
| ndarray.ndim | 数组维数 |
| ndarray.size | 数组中的元素数量 |
| ndarray.itemsize | 一个数组元素的长度(字节) |
| ndarray.dtype | 数组元素的类型 |
2、形状修改
ndarray.reshape(shape):返回一个具有相同数据的新数组
ndarray.resize(shape):无返回值,对原来的数组改变形状
# 例一
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
a.reshape((4, 3))
# 输出
array([[1, 2, 3], # shape改为4*3
[3, 4, 5],
[6, 6, 7],
[8, 9, 9]])
# 例二
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
a.reshape((2, -1)) # -1代表行或列待计算
# 输出
array([[1, 2, 3, 3, 4, 5], # shape改为2*6
[6, 6, 7, 8, 9, 9]])
# 例三
a.resize((6, 2))
a
# 输出
array([[1, 2],
[3, 3],
[4, 5],
[6, 6],
[7, 8],
[9, 9]])
3、类型修改
ndarray.astype(type):返回修改了类型之后的一个新数组
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
a.astype(np.float16)
a
# 输出
array([[1., 2., 3., 3.],
[4., 5., 6., 6.],
[7., 8., 9., 9.]], dtype=float16)
array([[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
三、numpy基本操作
1、生成数组
①生成0,1数组
np.ones和np.zeros
np.ones((3, 3), dtype = np.int64)
array([[1, 1, 1], # 输出
[1, 1, 1],
[1, 1, 1]], dtype=int64)
np.zeros((3, 3), dtype = np.float64)
array([[0., 0., 0.], # 输出
[0., 0., 0.],
[0., 0., 0.]])
②从现有数组中生成
np.array和np.asarray
a = np.array([[1,2,3],[4,5,6]])
a1 = np.array(a) # 深拷贝
a2 = np.asarray(a) # 浅拷贝
③生成固定范围的数组
np.linspace
np.linspace (start, stop, num):从start到stop按等差数列分割为num个数,左闭右闭,num默认为50
np.linspace(0, 100, 11)
# 输出
array([ 0., 10., 20., 30., 40., 50., 60., 70., 80., 90., 100.])
np.arange
np.arange(start,stop, step, dtype):将start到stop每隔step的步长的数取出,左闭右开,step默认为1
np.arange(0, 10, 2)
# 输出
array([0, 2, 4, 6, 8])
np.logspace
np.logspace(start,stop, num):从start到stop按等比数列分割num个数,左闭右闭,num默认为50
np.logspace(0, 2, 3) # 生成10^x
# 输出
array([ 1., 10., 100.])
④生成随机数组
正态分布和np.random.normal
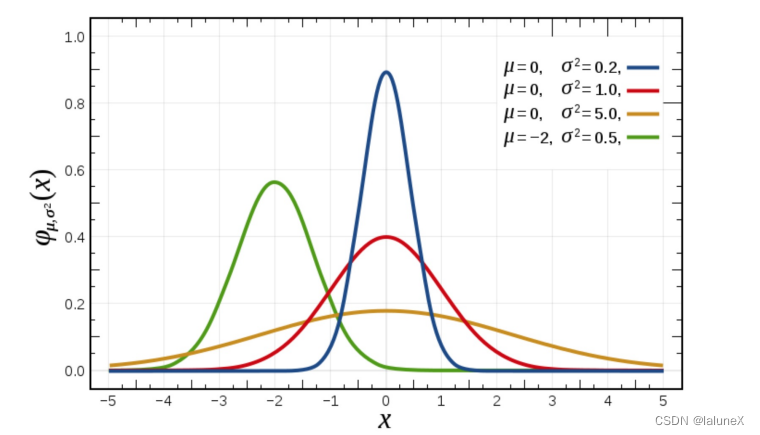
正态分布是具有两个参数μ和σ的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ是此随机变量的方差,所以正态分布记作N(μ,σ )。
其中μ决定了其位置,其标准差σ决定了分布的胖瘦。且当μ = 0,σ = 1时的正态分布是标准正态分布。
σ越小分布则越瘦高,σ越大分布则越矮胖
np.random.normal(loc=0.0, scale=1.0, size=None):从正态分布中返回一个或多个样本值,每次执行返回的值不一定相同
参数:
loc(float):此概率分布的均值(对应着整个分布的中心centre)
scale(float):此概率分布的方差(对应于分布的宽度,scale越大越矮胖,scale越小越瘦高)
size(int or tuple of ints):输出数据的shape,默认为None,只输出一个值
返回值:
ndarray类型,其形状和参数size中描述一致。
np.random.normal(0, 1, (10,))
# 输出
array([ 1.21557398, 1.09191592, -0.46836205, 0.75189818, -0.46659718,
0.06309407, 0.00794335, 1.79740285, 0.91503539, 0.73752313])
np.random.normal(0, 1, (2, 5))
# 输出
array([[-0.31547475, 1.15872105, -0.26802975, 0.80356083, 0.10224048],
[ 1.60132828, 1.34053389, -0.94250032, -0.35546642, -0.35632314]])
均匀分布和np.random.uniform
np.random.uniform(low=0.0, high=1.0, size=None):从一个均匀分布 [low,high)中随机采样,注意定义域是左闭右开,即包含low,不包含high。
参数:
low:采样下界,float类型,默认值为0;
high:采样上界,float类型,默认值为1;
size:输出样本数目,为int或元组(tuple)类型,缺省时输出1个值。
返回值:
ndarray类型,其形状和参数size中描述一致。
y = np.random.uniform(-1, 1, (2, 2))
# 输出
array([[ 0.14440759, -0.72418455],
[ 0.57956982, -0.75909833]])
2、数组的去重
np.unique():将数组去重后,返回一个新的数组
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
np.unique(a)
# 输出
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
3、判断函数
np.all():判断数组是否都满足条件
np.any():判断数组是否有满足条件的数据
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
np.all(a > 5)
np.any(a > 5)
# 输出
False
True
4、三元运算符
np.where(condition, [x, y]):三元运算符,可以搭配np.logical_and和np.logical_or使用
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
np.where(a >= 5, 1, 0)
np.where(np.logical_and(a >= 5, a <= 6), 1, 0)
# 输出
array([[0, 0, 0, 0],
[0, 1, 1, 1],
[1, 1, 1, 1]])
array([[0, 0, 0, 0],
[0, 1, 1, 1],
[0, 0, 0, 0]])
5、统计
在这里,axis=0代表列, axis=1代表行去进行统计
np.max(temp, axis=0):最大值
np.min(temp, axis=0):最小值
np.mean(temp, axis=0):平均值
np.std(temp, axis=0):标准差
四、运算
1、数组与数
a = np.array(
[[1, 2, 3, 3],
[4, 5, 6, 6],
[7, 8, 9, 9]])
a * 2
# 输出
array([[ 2, 4, 6, 6],
[ 8, 10, 12, 12],
[14, 16, 18, 18]])
2、python中np.multiply()、np.dot()、星号(*)和@运算符的区别
①np.multiply()
数组和矩阵对应位置相乘,输出与相乘数组/矩阵的大小一致
②np.dot():点乘
对于秩为1的数组,执行对应位置相乘,然后再相加
对于秩不为1的二维数组,执行矩阵乘法运算
对于矩阵,则运行矩阵的乘法
③星号(*)
对数组执行对应位置相乘
对矩阵执行矩阵乘法运算
④@运算符
是矩阵的乘法运算符
五、其他内容
1、方差
方差为每个样本值与全体样本值的平均数之差的平方值的平均数,方差越大数据波动也就越大
δ 2 = ∑ i = 1 n ( x i ? μ ) 2 n \delta^2=\frac{\sum_{i=1}^n(x_i-\mu)^2}{n} δ2=n∑i=1n?(xi??μ)2?
2、标准差(均方差)
是方差的算术平方根,标准差能反映一个数据集的离散程度。
σ = ∑ i = 1 n ( X i ? μ ) 2 n \sigma=\sqrt{\frac{\sum_{i=1}^n(X_i-\mu)^2}{n}} σ=n∑i=1n?(Xi??μ)2??
3、均方误差Mean square error(MSE)
均方误差是评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
M S E = ∑ i = 1 n [ f ( x i ) ? y i ] 2 n MSE=\frac{\sum_{i=1}^n[f(x_i)-y_i]^2}{n} MSE=n∑i=1n?[f(xi?)?yi?]2?
4、残差平方和
为了明确解释变量和随机误差各产生的效应是多少,统计学上把数据点与它在回归直线上相应位置的差异称为残差,把每个残差平方之后加起来 称为残差平方和,它表示随机误差的效应。 一组数据的残差平方和越小,其拟合程度越好
∑ i = 1 n [ h θ ( x i ) ? y i ] 2 \sum_{i=1}^n[h_\theta(x_i)-y_i]^2 ∑i=1n?[hθ?(xi?)?yi?]2
5、广播机制
数组在进行矢量化运算时,要求数组的形状是相等的。当形状不相等的数组执行算术运算的时候,就会出现广播机制,该机制会对数组进行扩展,使数组的shape属性值一样,这样,就可以进行矢量化运算了。下面通过一个例子进行说明:
arr1 = np.array([[0],[1],[2],[3]])
arr1.shape
# (4, 1)
arr2 = np.array([1,2,3])
arr2.shape
# (3,)
arr1+arr2
# 输出
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 5],
[4, 5, 6]])
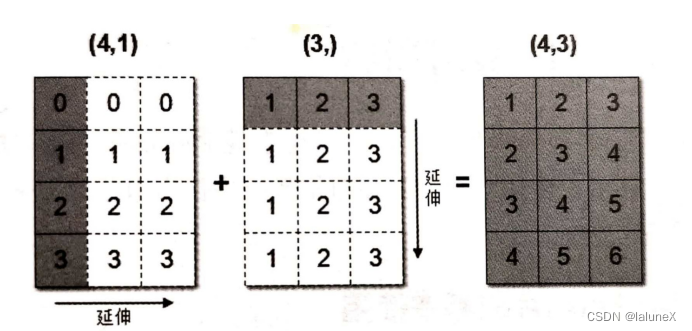
上述代码中,数组arr1是4行1列,arr2是1行3列。这两个数组要进行相加,按照广播机制会对数组arr1和arr2都进行扩展,使得数组arr1和arr2都变成4行3列。
运算过程:
广播机制发生条件(只需要满足如下任意一个条件即可,而且需要对每一维进行查看):
- 两个数组的某一维度等长
- 其中的一个数组的某一维度为1(如上例)
# 此时A,B不可广播,因为第二维不满足条件
A (1d array): (1, 10)
B (1d array): (1, 12)
# 此时A,B不可广播,因为第一维和第三维不满足条件
A (2d array): (2, 1)
B (3d array): (8, 4, 3)
# 此时A,B可广播
A (2d array): (2, 6)
B (3d array): (2, 1)
本文只用于个人学习与记录