开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 【机器学习】python实现非线性回归（以中国1960-2014GDP为例） -> 正文阅读

[人工智能]【机器学习】python实现非线性回归（以中国1960-2014GDP为例）

非线性回归

目标

区分线性回归和非线性回归
用py实现非线性回归

如果数据表现出一个曲线的趋势，那么相比于非线性回归，线性回归就不会产生一个非常精确的结果，因为线性回归假设数据是线性的。就让我们通过一个例子学习一下非线性回归。在这篇博客中我们对中国1960年到2014年的GDP拟合了一个非线性模型。

导入相关库

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

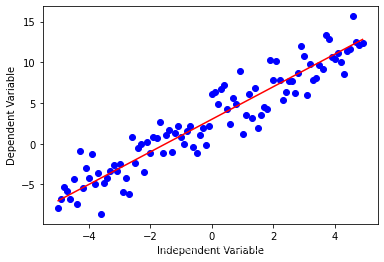
虽然线性回归在有的数据集上表现的很好，但是它不能应用到所有数据集。首先我们回想一下线性回归，它是拟合因变量y和自变量x，方程是很简单的，比如 $y = 2 x + 3$ 。

下面用代码来看看。

x = np.arange(-5.0, 5.0, 0.1)

##You can adjust the slope and intercept to verify the changes in the graph
y = 2*(x) + 3
y_noise = 2 * np.random.normal(size=x.size)
ydata = y + y_noise
#plt.figure(figsize=(8,6))
plt.plot(x, ydata,  'bo')
plt.plot(x,y, 'r') 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

请添加图片描述

非线性回归是用一种拟合自变量 $x$ 和因变量 $y$ 之间的非线性关系的一种方法。

比如下面是一个多项式。

$y = a x^3 + b x^2 + c x + d \$

非线性函数有指数、对数、分数等元素

$\log(x)$

也可以是这种复杂的形式
$y = \log(a x^3 + b x^2 + c x + d)$

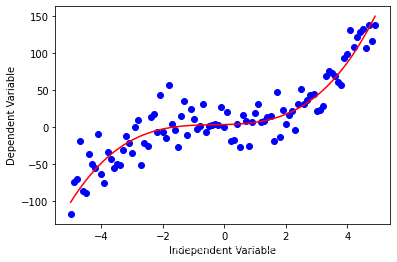
让我们看看这个三次函数

x = np.arange(-5.0, 5.0, 0.1)

##You can adjust the slope and intercept to verify the changes in the graph
y = 1*(x**3) + 1*(x**2) + 1*x + 3
# 加点噪音，也就是随机数
y_noise = 20 * np.random.normal(size=x.size)
ydata = y + y_noise
plt.plot(x, ydata,  'bo')
plt.plot(x,y, 'r') 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

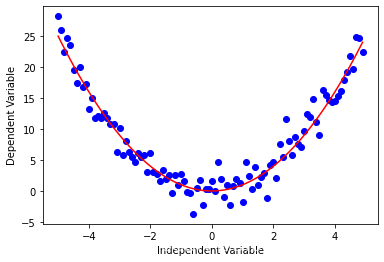
在这里插入图片描述

还有一些其他的形式

二次函数

$Y = X^2$

x = np.arange(-5.0, 5.0, 0.1)

##You can adjust the slope and intercept to verify the changes in the graph

y = np.power(x,2)
y_noise = 2 * np.random.normal(size=x.size)
ydata = y + y_noise
plt.plot(x, ydata,  'bo')
plt.plot(x,y, 'r') 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

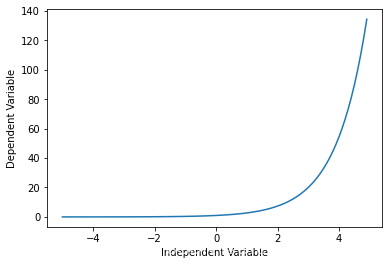
在这里插入图片描述

指数函数

$Y = a + b c^X$ $其中 b \neq = 0, c > 0, c \neq = 1$

X = np.arange(-5.0, 5.0, 0.1)

##You can adjust the slope and intercept to verify the changes in the graph

Y= np.exp(X)

plt.plot(X,Y) 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

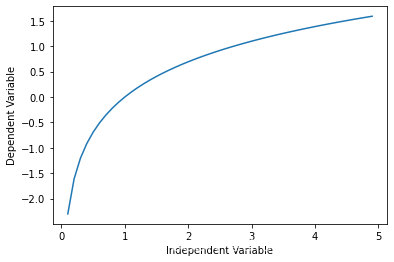
在这里插入图片描述

对数

$\log(x)$

X = np.arange(-5.0, 5.0, 0.1)

Y = np.log(X)

plt.plot(X,Y) 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

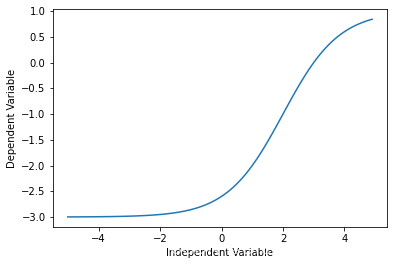
在这里插入图片描述

Sigmoidal/Logistic

$\frac{b}{1+ c^{(X-d)}}$

X = np.arange(-5.0, 5.0, 0.1)


Y = 1-4/(1+np.power(3, X-2))

plt.plot(X,Y) 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

在这里插入图片描述

非线性回归的例子

我们将要拟合中国从1960年到2014年的GDP数据。我们下载的数据有两列，第一列是年份，从1960到2014，第二列是对应年份的国内生产总值（美元）。

gdp数据（点我下载(?′?`?)）

import numpy as np
import pandas as pd
df = pd.read_csv("china_gdp.csv")
df.head(10)

	Year	Value
0	1960	5.918412e+10
1	1961	4.955705e+10
2	1962	4.668518e+10
3	1963	5.009730e+10
4	1964	5.906225e+10
5	1965	6.970915e+10
6	1966	7.587943e+10
7	1967	7.205703e+10
8	1968	6.999350e+10
9	1969	7.871882e+10

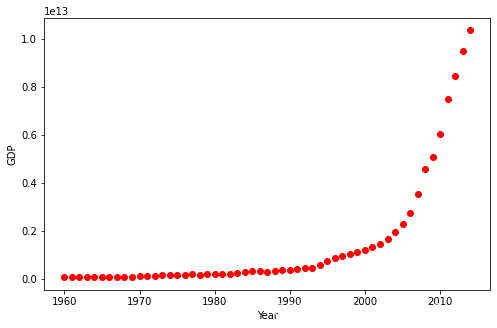
数据可视化

数据有点像logistic或者指数函数，一开始增长得特别慢，从2005年开始，增长速度就非常显著了，在2010年代略微减速。

plt.figure(figsize=(8,5))
x_data, y_data = (df["Year"].values, df["Value"].values)
plt.plot(x_data, y_data, 'ro')
# plt.stem(x_data, y_data)
plt.ylabel('GDP')
plt.xlabel('Year')
plt.show()

在这里插入图片描述

选择模型

从第一眼看这个散点图，我就感觉logistic函数会不错，因为一开始增长很慢、中间增长很快、最后又慢了下来

就像下面这样：

X = np.arange(-5.0, 5.0, 0.1)
Y = 1.0 / (1.0 + np.exp(-X))

plt.plot(X,Y) 
plt.ylabel('Dependent Variable')
plt.xlabel('Independent Variable')
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7EHjyekz-1655197597832)(output_28_0.png)]

logsitic函数的方程如下

$\hat{Y} = \frac1{1+e^{-\beta\_1(X-\beta\_2)}}$

$\beta\_1$ : 控制曲线的陡度,

$\beta\_2$ : x轴上平移

构建模型

现在，让我们构建我们的回归模型并且初始化参数

def sigmoid(x, Beta_1, Beta_2):
     y = 1 / (1 + np.exp(-Beta_1*(x-Beta_2)))
     return y

首先随便搞两个参数

beta_1 = 0.10
beta_2 = 1990.0

#logistic function
Y_pred = sigmoid(x_data, beta_1 , beta_2)

#plot initial prediction against datapoints
plt.plot(x_data, Y_pred*15000000000000.)
plt.plot(x_data, y_data, 'ro')

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fdiZTFbv-1655197597833)(output_33_1.png)]

我们的目标是找到最好的参数。

第一步把x和y都标准化一下。

# Lets normalize our data
xdata =x_data/max(x_data)
ydata =y_data/max(y_data)

如何找到拟合曲线最好的参数？

我们可以使用curve_fit，它使用非线性最小二乘来拟合我们的sigmoid函数。优化参数值，使sigmoid(xdata， *popt) - ydata的残差平方和最小化。

Popt是我们的优化参数。

from scipy.optimize import curve_fit
popt, pcov = curve_fit(sigmoid, xdata, ydata)
#print the final parameters
print(" beta_1 = %f, beta_2 = %f" % (popt[0], popt[1]))

 beta_1 = 690.451711, beta_2 = 0.997207

现在画一下我们的回归模型。

x = np.linspace(1960, 2015, 55)
x = x/max(x)
plt.figure(figsize=(8,5))
y = sigmoid(x, *popt)
plt.plot(xdata, ydata, 'ro', label='data')
plt.plot(x,y, linewidth=3.0, label='fit')
plt.legend(loc='best')
plt.ylabel('GDP')
plt.xlabel('Year')
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PIAwrPIA-1655197597833)(output_39_0.png)]

评估模型

虽然看上去不错，但是在运行过程中 $R^2$ 有时竟是负的，而且就是 $R^2$ 很大的时候在测试集上实际效果也不是很好，所以还是不很靠谱。

# 把数据分为训练集和测试集
msk=np.random.rand(len(df))<0.8
# print(msk)
train_x=xdata[msk]
test_x=xdata[~msk]
train_y=ydata[msk]
test_y=ydata[~msk]

# 用训练集建立一个模型
popt,pcov=curve_fit(sigmoid,train_x,train_y)

yyy = sigmoid(train_x, *popt)
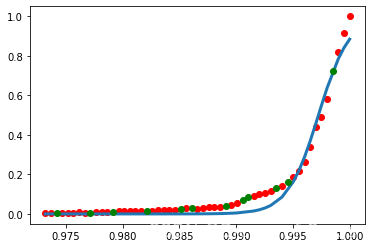
plt.plot(train_x, train_y, 'ro', label='data')
plt.plot(train_x,yyy, linewidth=3.0, label='fit')
plt.plot(test_x, test_y, 'go', label='data')
# 在测试集上预测
y_hat=sigmoid(test_x,*popt)
print("test_x:",test_x*sum(df["Year"]))
print("test_y:",test_y*sum(df['Value']))
print("y_hat:",y_hat*sum(df['Value']))
# 评估
print("Mean absolute error: %.2f" % np.mean(np.absolute(y_hat - test_y)))
print("Residual sum of squares (MSE): %.2f" % np.mean((y_hat - test_y) ** 2))
from sklearn.metrics import r2_score
print("R2-score: %.2f" % r2_score(test_y,y_hat) )

test_x: [106463.34160874 106788.91757696 107005.96822244 107331.54419067
 107657.12015889 107765.64548163 108091.22144985 108254.00943396
 108308.27209533 108579.58540218 108688.11072493 109122.21201589]
test_y: [3.56342870e+11 5.34252726e+11 8.56103610e+11 1.13258445e+12
 1.96991285e+12 2.28075199e+12 3.24347532e+12 5.58752067e+12
 6.57072900e+12 1.01688021e+13 1.25937257e+13 5.71889161e+13]
y_hat: [3.13221434e+06 2.82948697e+07 1.22728310e+08 1.10865316e+09
 1.00138972e+10 2.08527024e+10 1.87974610e+11 5.62290529e+11
 8.08915481e+11 4.80484704e+12 9.38891854e+12 5.66862461e+13]
Mean absolute error: 0.03
Residual sum of squares (MSE): 0.00
R2-score: 0.96

在这里插入图片描述