自动调整学习速率
总结
为什么需要调整学习率?
critical point(驻点)其实不一定是在训练Network的时候会遇到的最大的障碍,有可能是梯度还很大但是训练停止了(在峡谷间震荡不能到峡谷底部),这是优化没有做好的问题。
单一固定(one-size-fits-all)的学习率Model训练到驻点很困难,学习率太大不能收敛,学习率太小收敛太慢。
参考:【AI不惑境】学习率和batchsize如何影响模型的性能? - 龙鹏-笔名言有三的文章 - 知乎
如何调整学习率?
引入参数σ。相关算法:
Adagrad - 不同参数不同学习率
RMSProp - 同一参数不同学习率
Adam - RMSProp + Momentum
为什么会梯度爆炸?
error surface 平滑区域,随着时间的增加,σ会越来越小,导致学习率增大,梯度爆炸。
如何解决梯度爆炸?
让时间影响学习率。使η随时间变化,相关算法:
方式一:Learning Rate Decay(学习速率衰减)
方式二:Warm Up(预热)
Training stuck ≠ Small Gradient(训练卡住不代表小梯度)- 有可能是梯度还很大但是训练停止了(在峡谷间震荡不能到峡谷底部)
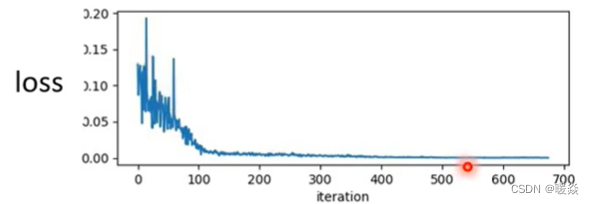
人们在训练一个network的时候往往会把它的loss记录下来,所以就会发现loss原来很大,上图横轴代表参数update的次数,随著参数不断的update,这个loss会越来越小,最后就卡住了,loss不再下降。
一般在遇到这个情况的时候人们大多都在猜想是不是走到了critical point,因为gradient为零,所以没有办法再更新参数。但是真的是这样吗? 当走到critical point的时候,意味著gradient非常的小,但是你有确认过loss不再下降的时候gradient真的很小吗?
实际上多数人都没有确认过这件事。
事实上在下面例子中,当loss不再下降的时候,gradient并不是真的变得很小。
当loss不再下降时,并不一定是gradient很小的情况(saddle point 或者 local minima),也有可能是gradient在error surface山谷的两个谷壁间不断的来回的震荡导致loss不能再下降。
为什么需要自动调整学习率?- 单一固定(one-size-fits-all)的学习率Model训练到驻点很困难(学习率太大不能收敛,学习率太小收敛太慢)
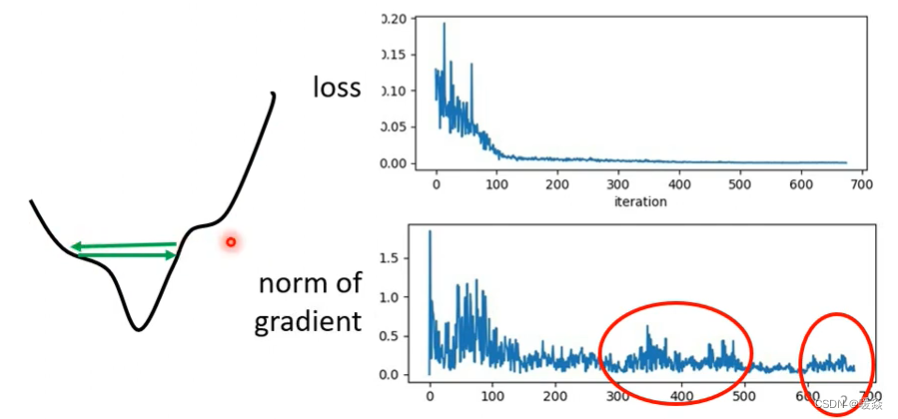
gradient是一个向量,上图中下面的图是gradient的norm(范数),即gradient这个向量的长度随参数更新时的变化。你会发现虽然loss不再下降,但是gradient的大小并没有真的变得很小。
也许遇到的是上图中左边这个曲线代表的情况。这个曲线是我们的error surface,现在gradient在error surface山谷的两个谷壁间不断的来回的震荡 这个时候loss不会再下降,所以你会觉得它真的卡在critical point。但实际上不是的,它的gradient仍然很大,只是loss不会再减小了。
所以要注意,训练一个network的时候,train到后来发现loss不再下降的时候不要随便说卡在驻点,有时候并不是卡在两类驻点上,只是单纯的loss没有办法再下降。
实际上,在真实的训练过程中,Model训练到驻点的位置是比较困难的事情,除非是用十分特殊的gradient descend train。大多数情况是在梯度还没有变小(或还没有训练到驻点)的时候训练就停下来了。
Training can be difficult even without critical points(即使没有驻点,训练也会很困难)
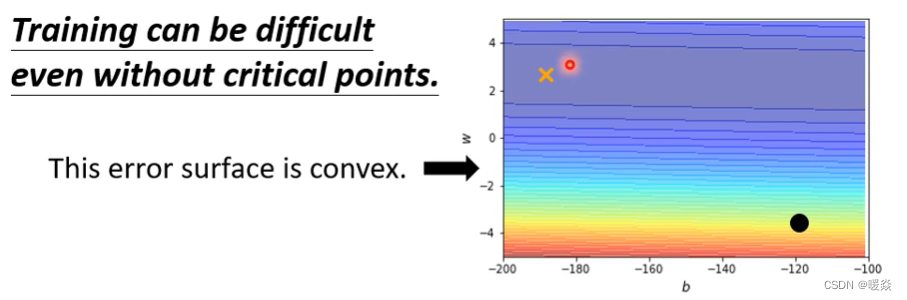
以上图为例子,只有两个参数,这两个参数值不一样的时候Loss的值不一样,画出了error surface,这个error surface的最低点在上图黄色X的地方。事实上,这个error surface是convex的形状(可以理解为凸的或者凹的,convex optimization常翻译为“凸优化”)。
总之它是一个椭圆形的等高线,只是在横轴的地方,它的gradient非常的小,它的坡度的变化非常的小、非常的平滑。所以这个椭圆的长轴非常的长,短轴相对之下比较短,在纵轴的地方gradient的变化很大,error surface的坡度非常的陡峭。
现在把上图中的黑点当作初始的点,来做gradient descend。 要注意,实际上这种convex的error surface,形状看上去比较简单的error surface用gradient descend不一定能把它做好。
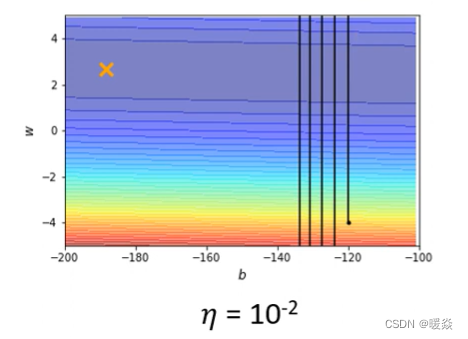
当learning rate设为10?2的时候,这个参数在峡谷的两端不断的震荡从而导致loss掉不下去,但此时的gradient仍然很大。
那你可能说是因为learning rate设太大了,learning rate决定了我们update参数的时候步伐有多大,learning rate步伐太大,没办法慢慢地滑到山谷里面,只要把learning rate设小一点不就可以解决这个问题了吗? 实则不然,因为当你试着去调整这个learning rate就会发现要train这种convex的optimization的问题非常麻烦,调这个learning rate从10?2一直调到10??终于不再震荡。
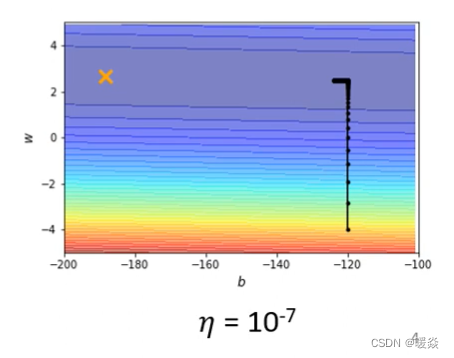
但是这个训练此时永远走不到终点,因为learning rate已经太小了,上图中垂直竖线,因为坡度很陡、gradient的值很大,所以还能够前进一点;左拐以后在横短黑线这个地方坡度已经非常平滑了,这么小的learning rate根本没有办法再让训练前进(
θ
i
+
1
=
θ
i
?
η
g
\theta_{i+1}=\theta_{i}-\eta g
θi+1?=θi??ηg)。
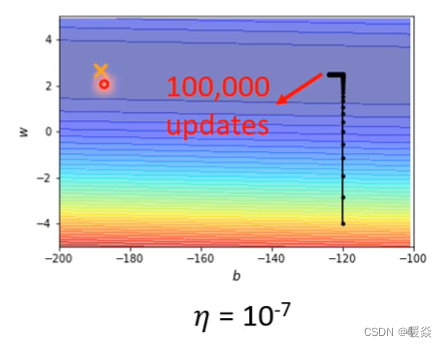
事实上在左拐这个地方,这一大堆黑点有十万个,所以显然就算是一个convex的error surface,你用gradient descend也很难train。
这个convex的optimization的问题确实有别的方法可以解,但是gradient descend这个工具连这么简单的error surface都做不好,那遇到难的问题时就更做不好了。
所以我们需要更好的gradient descend的方法,在之前的gradient descend中,所有的参数都是设同样的learning rate,这显然是不够的,learning rate它应该要根据不同的参数进行定制,也就是客制化。
如何客制化学习率?- 引入参数σ
Different parameters needs different learning rate(不同的参数需要不同的学习率)
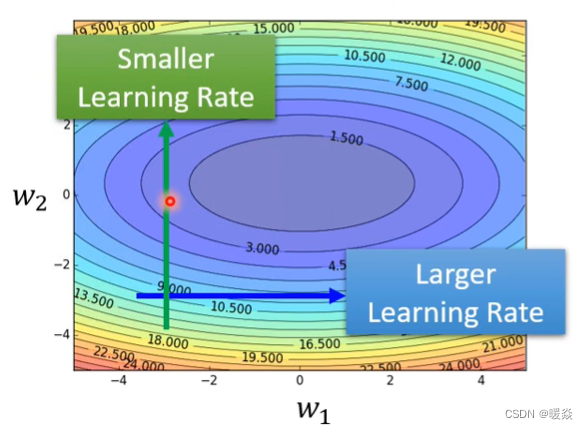
那客制化学习率的方法是什么? 从刚才的例子中,其实可以看到一个大原则,如果在某一个方向上的gradient的值很小,非常的平坦,那我们会希望learning rate调大一点;如果在某一个方向上非常的陡峭,坡度很大,那我们其实期待learning rate可以设得小一点。 也就是说希望学习率可以根据梯度的情况进行调整,就和下图一样
那这个learning rate要如何自动的根据gradient的大小做调整呢? 需要改进一下gradient descend原来的式子。为了方便起见先只看一个参数,但是可以推广到多个参数。(维度归一) 先看原本如何进行Update:
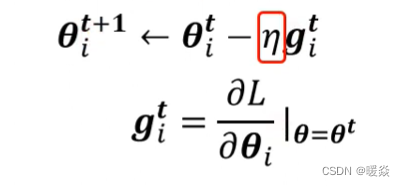
先只看一个参数θ,上图式子中的参数 θ i t \theta_i^t θit?为θ在第t个iteration(迭代)的值,减去学习率乘以在第t个iteration时参数 i 算出来的gradient,得到下一次迭代的参数值 θ i t + 1 \theta_i^{t+1} θit+1?,其中 g i t g_i^t git?代表在第t个iteration,也就是θ=θ?的时候,参数θ?对loss的微分。以上是原来的计算gradient descend的方法,learning rate是固定的。
现在要对上述方法进行改进,要对Learning rate进行客制化,把原来学习率μ这一项改写成 η σ i t \frac{\eta}{\sigma_i^t} σit?η?,原先的式子就变成了: θ i t + 1 = θ i t ? η σ i t g i t \theta_i^{t+1}=\theta_i^{t}-\frac{\eta}{\sigma_i^t}g_i^t θit+1?=θit??σit?η?git?。其中, σ i t \sigma_i^t σit?的上标t代表第t个iteration,下标i代表第i个参数,也就是说σ一方面依赖于迭代次数,迭代次数不同σ不同;另一方面说明σ也依赖于不同参数,参数不同σ也不同。
也就是说引进σ就可以把学习率改进成了parameter dependent(参数相关)的learning rate。
接下来看σ常见的计算方式。
σ常见的计算方式 - Root mean square(均方根)
计算σ的一个常见的类型是计算gradient的Root Mean Square。
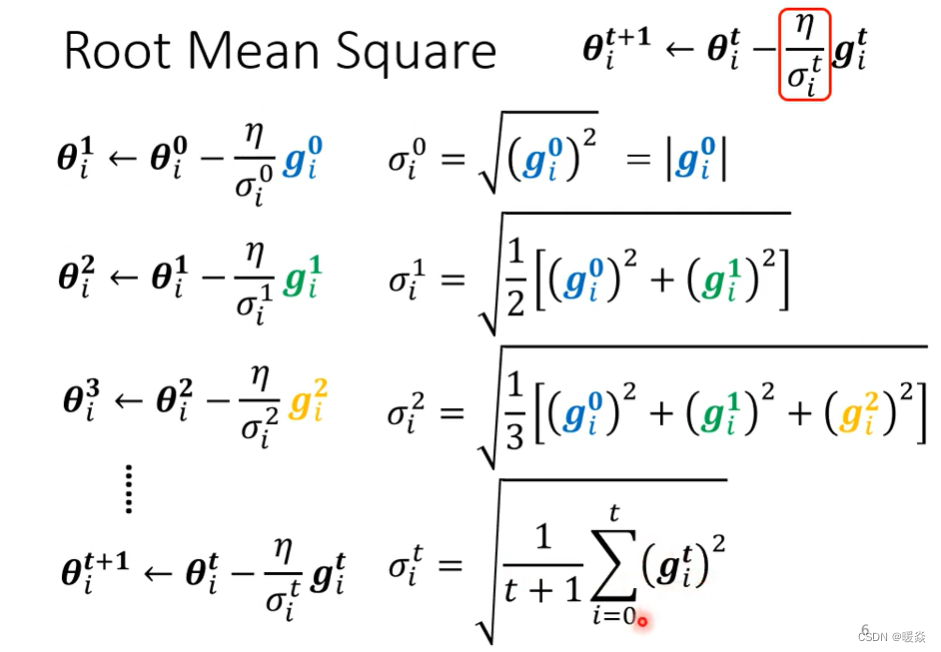
Adagrad - 不同参数不同学习率
上面这个方法被应用在Adagrad算法中,Adagrad是解决不同参数应该使用不同的更新速率的问题。Adagrad是自适应地为各个参数分配不同学习率的算法。
为什么这一招可以做到当坡度比较大的时候learning rate就减小,坡度比较小的时候learning rate就放大呢?
你可以想像说,现在有两个参数:一个叫θ?1,一个叫θ?2 。θ?1坡度小,θ?2坡度大
- θ?1因为它坡度小,所以在θ?1这个参数上面算出来的gradient值都比较小。
- 因为gradient算出来的值比较小,并且σ公式可以知道,σ计算结果就比较小。
又因为Learning rate的计算方法被改进为 η σ i t \frac{\eta}{\sigma_i^t} σit?η?,σ小导致学习率就大。
所以有了σ这一项以后,就可以随著每一个参数的gradient的不同,来自动的调整learning rate的大小。但这个方法还有改进的余地。
RMSProp - 同一参数不同学习率
root mean square prop:均方根传递
我们期望:就算是同一个参数,它需要的learning rate也会随著时间而改变。
上面的方法中,同一个参数,其gradient的大小差不多。但事实上并不是这样,比如下图这个例子,心月形的error surface
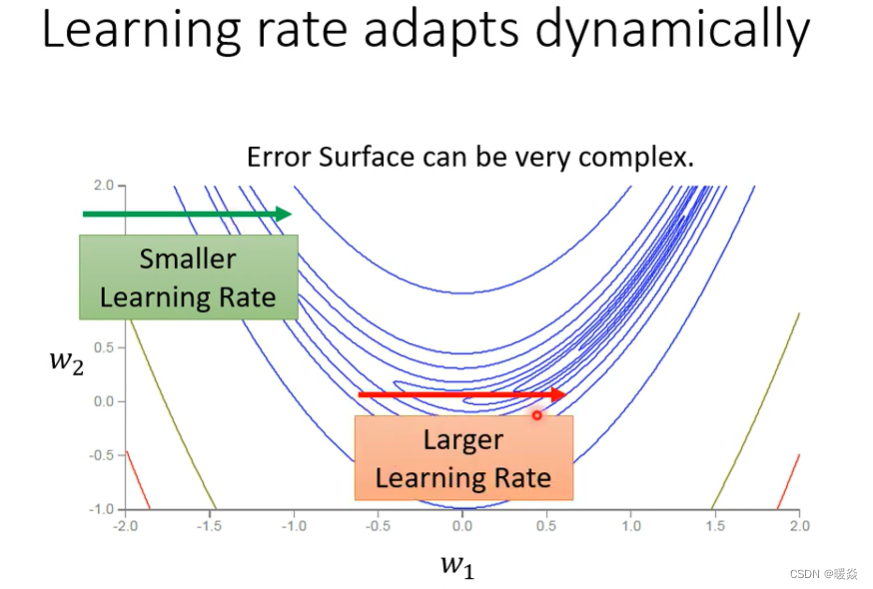
如果考虑横轴的方向的话,会发现在绿色箭头这个地方坡度比较陡峭,所以我们需要比较小的learning rate。
但是走到红色箭头的时候,坡度又变得平滑了起来,平滑就需要比较大的learning rate。
红色和绿色线的方向,可以看做同一个参数w2的同一个方向,所以就算是同一个参数的同一个方向,也需要learning rate可以动态的调整。于是就有了RMS Prop。
RMS Prop 不是出自论文,只是Hinton在自己的deep learning课程中提出的。
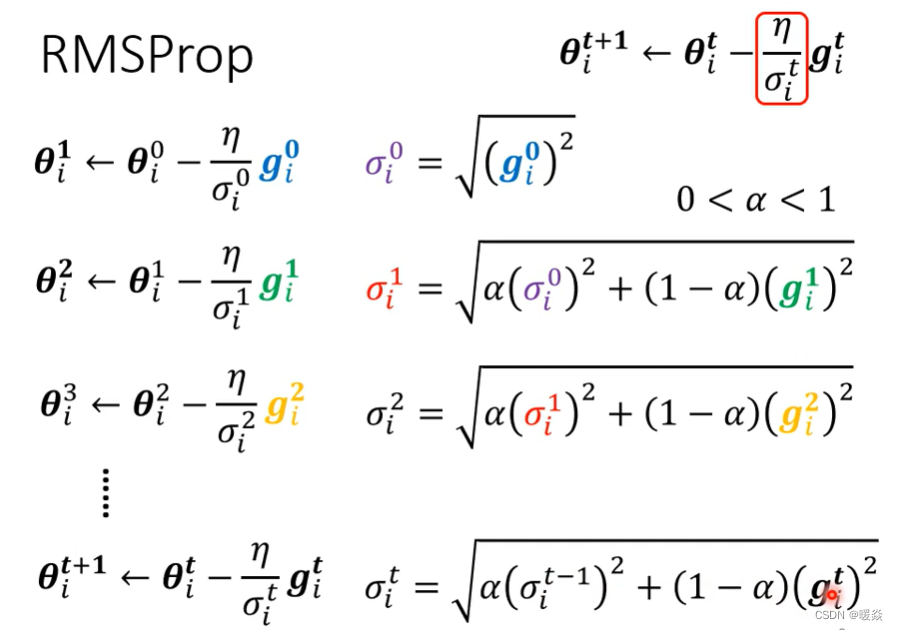
RMS Prop它的第一步跟Root Mean Square,也就是Apagrad的方法是一模一样的。
第二步中,一样要算出σ?1,只是我们现在算出σ?1的方法跟刚才算Root Mean Square的时候不一样。刚才在算Root Mean Square的时候,每一个gradient都有同等的重要性,但在RMS Prop中,你可以自己调整gradient的重要性或权重。
α就像learning rate一样,需要人工调整,是一个hyperparameter。
- 如果α设很小趋近于0,就代表g?1相较于之前所算出来的gradient,比较重要
- 如果α设很大趋近于1,那就代表迭代中当前算出来的g?1不重要,之前算出来的gradient比较重要。
之后以此类推,你用α来决定现在当前算出来的g??的重要性,这个方法也就是RMSProp。
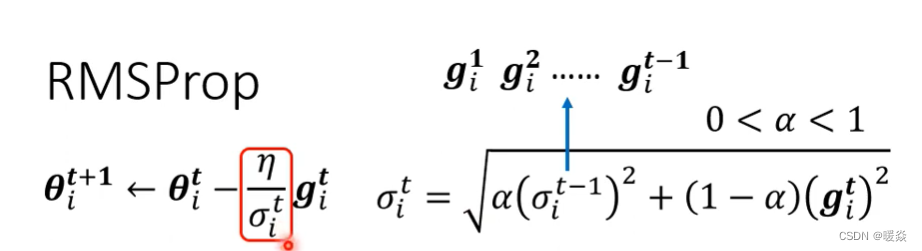
综上所述,RMSProp透过α可以决定g??相较于之前存在于σ???1中的g?1、g?2、g?3、……、g???1它的重要性有多大。如果用RMS Prop的话,就可以动态调整σ这一项。
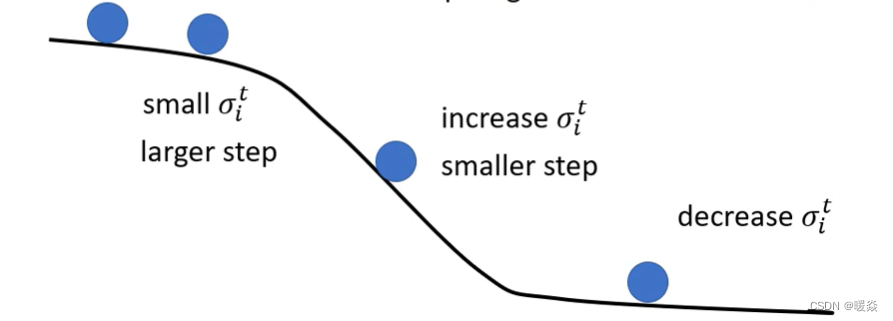
上图的黑线是error surface,从左边第一个蓝球开始要update参数,也就是这个蓝球滚到第二个蓝球的地方,因为一路上都很平坦,就代表说g算出来很小,也就代表现在update参数的时候会走的步伐比较大。
接下来继续滚,滚到第三个蓝球以后gradient变大了。如果不用RMS Prop,采用原来的Adagrad的话它反应比较慢,但如果用RMS Prop,把α设小一点
也就是此时的gradient影响比较大的话,那就可以通过将α的值调小,从而让σ的值变大,可以很快的让你的步伐变小。
也就是说通过RMSProp,在第三个蓝球这里可以给Mosel的Update踩一个煞车,把learning rate变小;如果没有踩剎车的话,走到第三个蓝球这里learning rate太大了,那gradient又很大,两个很大的东西乘起来,可能就很快就飞出去了,飞到很远的地方。
如果继续走,又走到第四个蓝球这里,是一个平滑的地方,因为在σ?? 中可以调整α,让它比较看重最近算出来的gradient,所以gradient一变小,σ反应很快,它的值就变小了。然后走的步伐就变大了,这个就是RMS Prop的具体过程。
Adam:RMSProp + Momentum
Adam是现在最常用的optimization的策略。

Adam就是RMS Prop加上Momentum,Adam的演算法跟原始的论文https://arxiv.org/pdf/1412.6980.pdf
在pytorch中都帮你把算法写好了,所以不用担心这种optimization的问题。optimizer的deep learning套件往往都做好,然后这个optimizer里面也有一些hyperparameter需要人工决定,但是你往往用预设的那一种参数就可以了,自己调有时候会调到比较差的。
Learning Rate Scheduling(学习速率调度)
没有学习率调整
?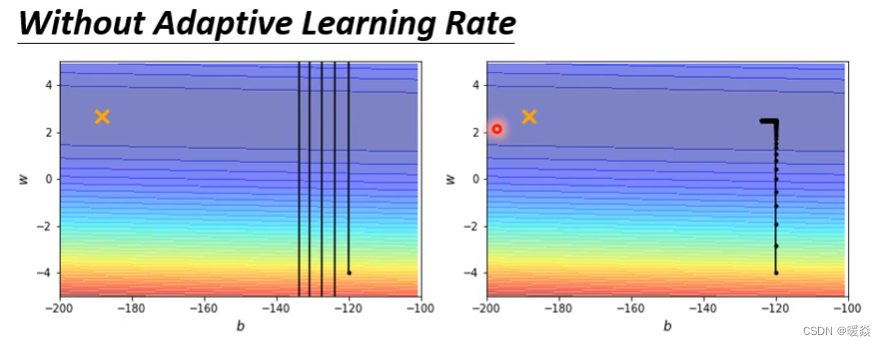
开始的例子中,这个简单的error surface我们都train不起来,现在来看一下加上Adaptive Learning Rate以后能不能训练的起来。
使用Adagrad的问题 - 梯度爆炸
先用最原始的Adagrad的方法,做起来是这个样子的
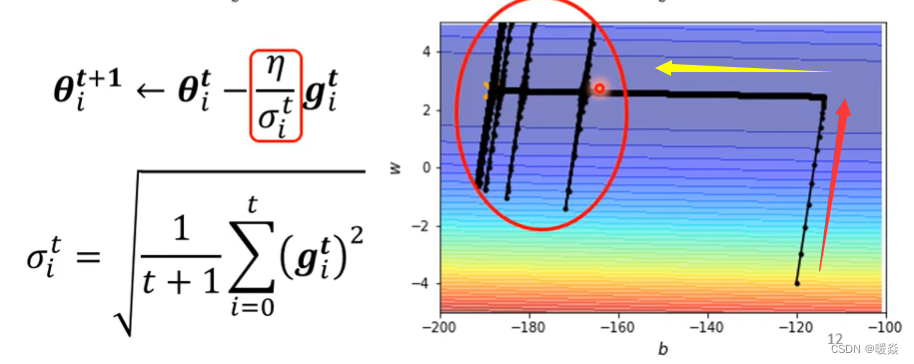
上图右边error surface是采用Adagrad的方法的结果。
可以看到相比较以前的方法,黄色箭头就是改进的地方,原先训练十万次就只能走蓝色箭头这么长,但是采用Adagrad的方法后,训练十万次可以走黄色箭头这么长。
那现在有Adagrad以后,可以再继续走下去,走到非常接近终点的位置,因为当走到红箭头到黄箭头拐角这个地方的时候,由于此时水平方向的gradient很小,所以会自动调整水平这个方向的learning rate,会自动变大,所以步伐就可以变大,就可以不断的前进。
什么是梯度爆炸?

因为在纵轴的方向上累积了很小的σ,累积到一个地步以后,这个step,也就是
η
σ
i
t
\frac{\eta}{\sigma_i^t}
σit?η?,就变得很大,然后就爆发了。
为什么会梯度爆炸?- 小梯度累加导致学习率突增
接下来的问题就,为什么快走到终点(上图红圈)的时候突然爆炸了呢?
因为在计算σ的时候,是把过去所有看到的gradient都拿来作平均
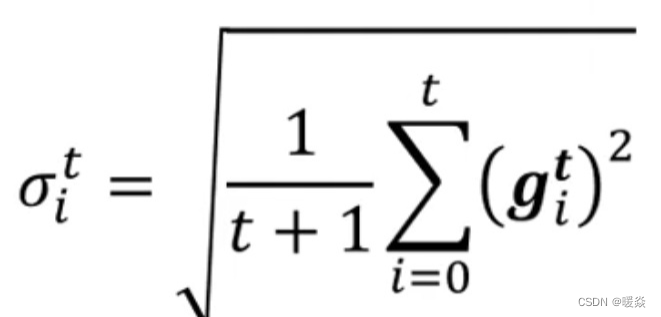
- 在纵轴的方向上,在初始的这个地方(红色箭头)gradient很大。
- 在横轴的方向上,黄色箭头方向,纵轴的方向不是没有gradient,只是gradient算出来都很小,所以在纵轴这个方向上就累积了很小的σ。(每次迭代累加很小的g,但是t每次都加1,σ会越来越小)
因为在纵轴的方向上累积了很小的σ,累积到一个地步以后,这个step,也就是 η σ i t \frac{\eta}{\sigma_i^t} σit?η?,就变得很大,然后就爆发了。
爆发了没有关系,还有办法修正回来(自动),因为爆发以后纵轴的gradient又变得比较大,这个σ又慢慢的变大,σ慢慢变大以后,这个参数update的步伐大小就又慢慢的变小。
就发现说走着走着,突然往左右喷了一下,但是不会永远就是在那里震荡停不下来。这个力道会慢慢变小,因为有摩擦力让它慢慢地慢慢地回到中间这个峡谷来,但是之后又累计一段时间以后又会爆发,然后又慢慢地回来。
如何处理梯度爆炸?- 让时间影响学习率
如何处理这种“爆发”问题,有一个方法叫做learning rate scheduling可以解决。
在原先的公式中:
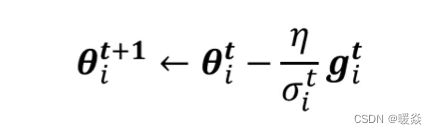
有一项η,η是一个固定的值。在learning rate scheduling中,不要把η当一个常数,要把它与时间建立联系
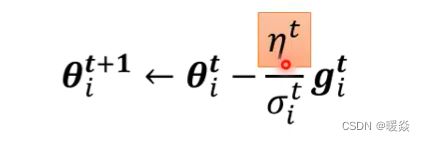
如何让时间影响学习率? - 方式一:Learning Rate Decay(学习速率衰减)
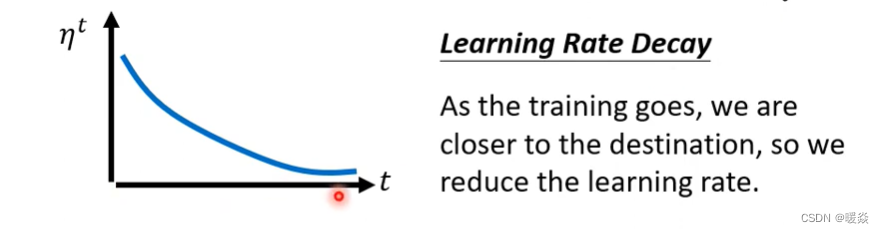
最常见的方法叫做Learning Rate Decay(学习速率衰减),也就是说随着时间的不断地前进、随着参数不断的update,让η越来越小。
那这个也就合理了,因为一开始距离终点很远,随著参数不断update,距离终点越来越近。所以把learning rate减小,让参数的更新踩一个煞车,让参数的更新能够慢慢地慢下来。所以刚才那个“爆炸”的状况,可以通过加上Learning Rate Decay来解决。
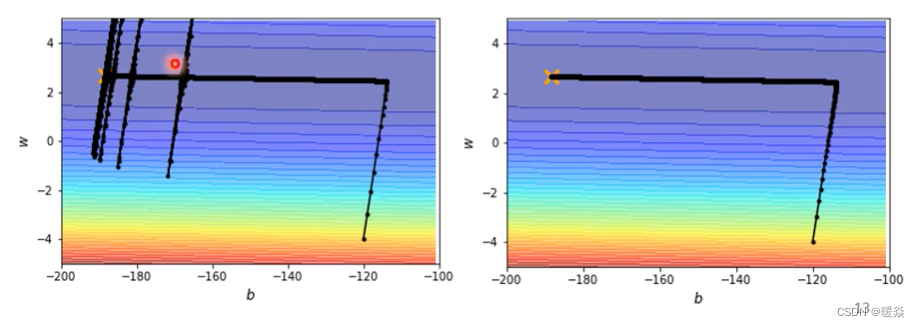
刚才那个状况如果加上Learning Rate Decay的话,就可以很平顺的走到终点,就是上图右下角的曲线。因为在原本要爆炸的地方,η已经变得非常的小了,虽然它本来想要左右乱喷,但是因为ηT的存在,就可以慢慢地走到终点。
如何让时间影响学习率? - 方式二:Warm Up(预热)
除了Learning Rate Decay以外,还有另外一个经典的、常用的Learning Rate Scheduling的方式,叫做Warm Up(预热)。
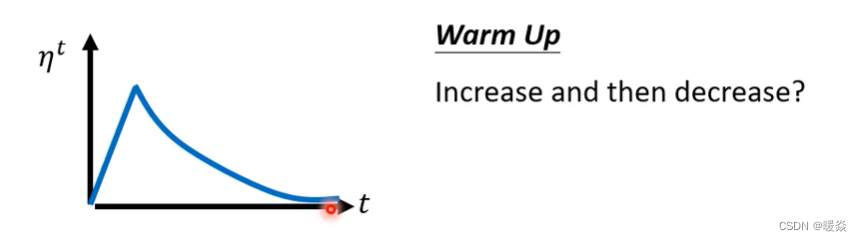
Warm Up这个方法听起来有点匪夷所思,这个方法是让learning rate要先变大后变小。其中变大变小的程度、速度都属于hyperparameter,要自己手动调,但是大方向的大策略就是learning rate要先变大后变小。
那这个方法听起来很神奇,就是一个黑科技,这个黑科技出现在很多远古时代的论文中。
因为在训练BERT(Bidirectional Encoder Representation from Transformers,是一个预训练的语言表征模型)的时候往往需要用到Warm Up,但并不是有BERT以后才有Warm Up的。Warm Up这东西很久之前就有了,举例来说Residual Network(剩余网络)中是有Warm Up的。

transformer 这篇论文中,也有warm up。

为什么warm up会起作用?- 待研究
一个可能的解释:σ是一个统计量,刚开始时,因为σ没有收集到足够的数据,先让η很小,学习率很小,步子很小,让σ有足够的时间收集更多的error surface的情况,等到σ收集到足够的情况可以做出很好的统计。更多关于warm up的资料参考:Radam论文
Summary of Optimization
最原始的gradient descent
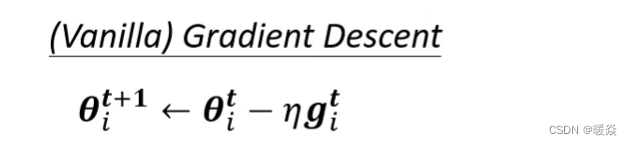
所以我们从最原始的gradient descent进化到这一个版本:

最新版本中有Momentum,也就是说现在不是完全顺著这一个时间点算出来的gradient的方向来update参数,而是把过去所有算出来gradient的方向,做一个加总当作update的方向,即momentum接下来应该要update多大的步伐则通过Root Mean Square。
这边可能有个困惑,momentum是考虑过去所有的gradient,σ也是考虑过去所有的gradient,一个放在分子一个放在分母,都考虑过去所有的gradient,不就是正好抵消了吗?
其实Momentum与σ,它们在使用过去所有gradient的方式是不一样的,Momentum是直接把所有的gradient通通都加起来,所以它有考虑方向,也就是gradient的正负号,它有考虑gradient是往左走还是往右走。
但是Root Mean Square就不考虑gradient的方向了,它只考虑gradient的大小,把gradient取一个平方项,是把平方的结果加起来,所以只考虑gradient的大小,不考虑它的方向。
所以Momentum跟σ算出来的结果并不会互相抵消。
那最后我们还会加上一个learning rate scheduling,
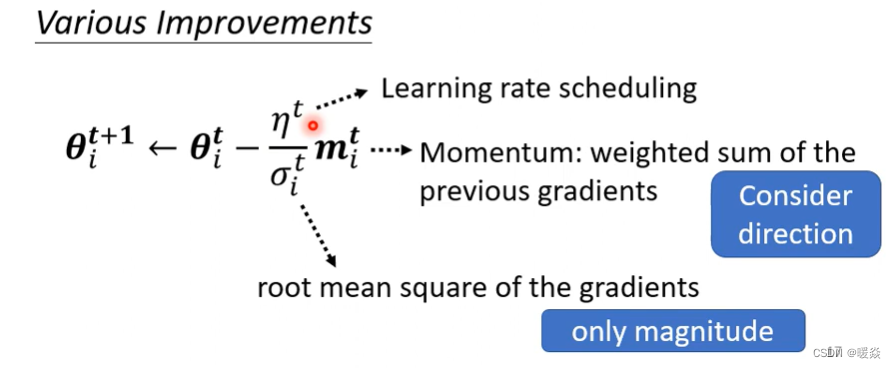
这个是现在optimization的完整的版本了。