1. 问题分析

1.1 问题描述

其实这个问题很简单，本篇博客全当备忘录了。我们的需求是：

在这里插入图片描述

图片来源：李沐：《动手学深度学习 PyTorch版》

1.2 解决思路

我们使用pytorch的自动微分机制来实现，我第一次是这么写的：

import torch

x = torch.arange(-5, 5, 0.01, requires_grad=True)
y = torch.sin(x)
y.backward()
print("f(x)=sin(x)的导数为：{}".format(x.grad))

结果报错了：

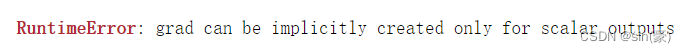
在这里插入图片描述
原因是这里的y是一个向量，而在使用y.backward()这个方法时，若backward中没有传入gradient这个参数时，只允许y是标量。事实上当x和y都是向量时，y对x求导得到的是一个矩阵（雅各比矩阵），我在这篇博客中有一些介绍：向量对向量求导，得到雅各比矩阵。

解决方法其实相当简单，本质思路是：将向量y转换为标量，然后使用标量的y进行y.backward()。

那么如何转换呢？其实只需对向量y的每一项进行求和即可，标量对向量的求导还是向量，设向量x=[x1, x1, …, xn]，向量y=[sin(x1), sin(x2), …, sin(xn)]，我们将向量y的每一项求和，得到标量y1=sin(x1)+sin(x2)+…+sin(xn)，最后用标量y1对向量x求导，即可得到向量d(y1)=[cos(x1), cos(x2), …, cos(xn)]，代码如下：

import torch

x = torch.arange(-5, 5, 0.1, requires_grad=True)
y = torch.sin(x)
y1 = y.sum()
y1.backward()
print("f(x)=sin(x)的导数为：\n{}".format(x.grad))

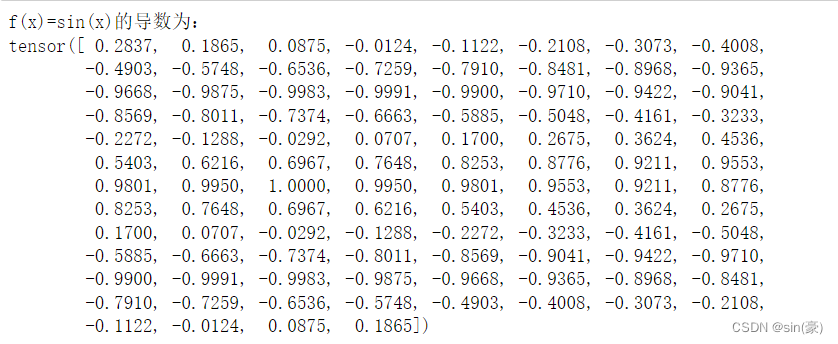
在这里插入图片描述

2. 代码实现

def get_derivative_tensor(x):
    x = torch.tensor(x, requires_grad=True)
    y1 = torch.sin(x)
    y1.sum().backward()
    return x.grad

x = np.arange(-5, 5, 0.01)
y = np.sin(x)

plt.plot(x, y, label='sin(x)')
dx = get_derivative_tensor(x)
plt.plot(x, dx.numpy(), label='dx')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.show()