矩阵 / 图像 坐标旋转
- 定义旋转矩阵,对2D的Tensor操作时,shape应当为
[B,2,3]
import math
from torch.nn import functional as F
B = 1 # batch size
# 初始化一个旋转角度
angle = 45/180*math.pi
# 创建一个坐标变换矩阵
transform_matrix = torch.tensor([
[math.cos(angle),math.sin(-angle),0],
[math.sin(angle),math.cos(angle),0]])
# 将坐标变换矩阵的shape从[2,3]转化为[1,2,3],并重复在第0维B次,最终shape为[B,2,3]
transform_matrix = transform_matrix.unsqueeze(0).repeat(B,1,1)
- 输入图像src,shape为
[H,W],需要将其转换成Tensor后的shape为[B,C,H,W]:(这里做旋转时有一个非常重要的大坑细节:旋转时务必先将tensor转换为正方形,即H=W,否则非正方形旋转会导致较长边出现拉伸情况。)- 如果输入src的
H,W不相等,首先需要做padding将其补全为正方形,同时要保证旋转中心点不变,再进行操作,最后将output的tensor中padding部分去除即可,padding操作如下所示。
- 如果输入src的
# [H,W] ——> [B,C,H,W]
src = torch.tensor(src, dtype=torch.float32).unsqueeze(0).unsqueeze(0)
如果需要padding:(假设src的shape为[1,1,400,200])
B,C,H,W = src.shape #
# padding
pad_list = torch.split(tensor=(torch.zeros_like(src, device=src.device, dtype=src.dtype)),
split_size_or_sections=[int(W/2),int(W/2)],
dim=-1)
src= torch.cat([pad_list[0], src, pad_list[1]], dim=-1)
src.shape # [1,1,400,400]
- 基于torch函数
affine_grid和grid_sample实现仿射变换:
# transform_matrix的shape为[B,2,3]
# 变换后tensor的shape与输入tensor相同
grid = F.affine_grid(transform_matrix, # 旋转变换矩阵
src.shape) # 变换后的tensor的shape(与输入tensor相同)
output = F.grid_sample(src, # 输入tensor,shape为[B,C,W,H]
grid, # 上一步输出的gird,shape为[B,C,W,H]
mode='nearest') # 一些图像填充方法,这里我用的是最近邻
# 输出output的shape为[B,C,W,H]
如果上一步你进行了padding操作,那么需要取出原src部分:
output = torch.split(output, # 经过仿射变换后的tensor, shape为[1,1,400,400]
split_size_or_sections=[int(W/2), int(W),int(W/2)], # 将其分离为三部分
dim=-1)[1]
output.shape # 输出output的shape为[1,1,400,200]
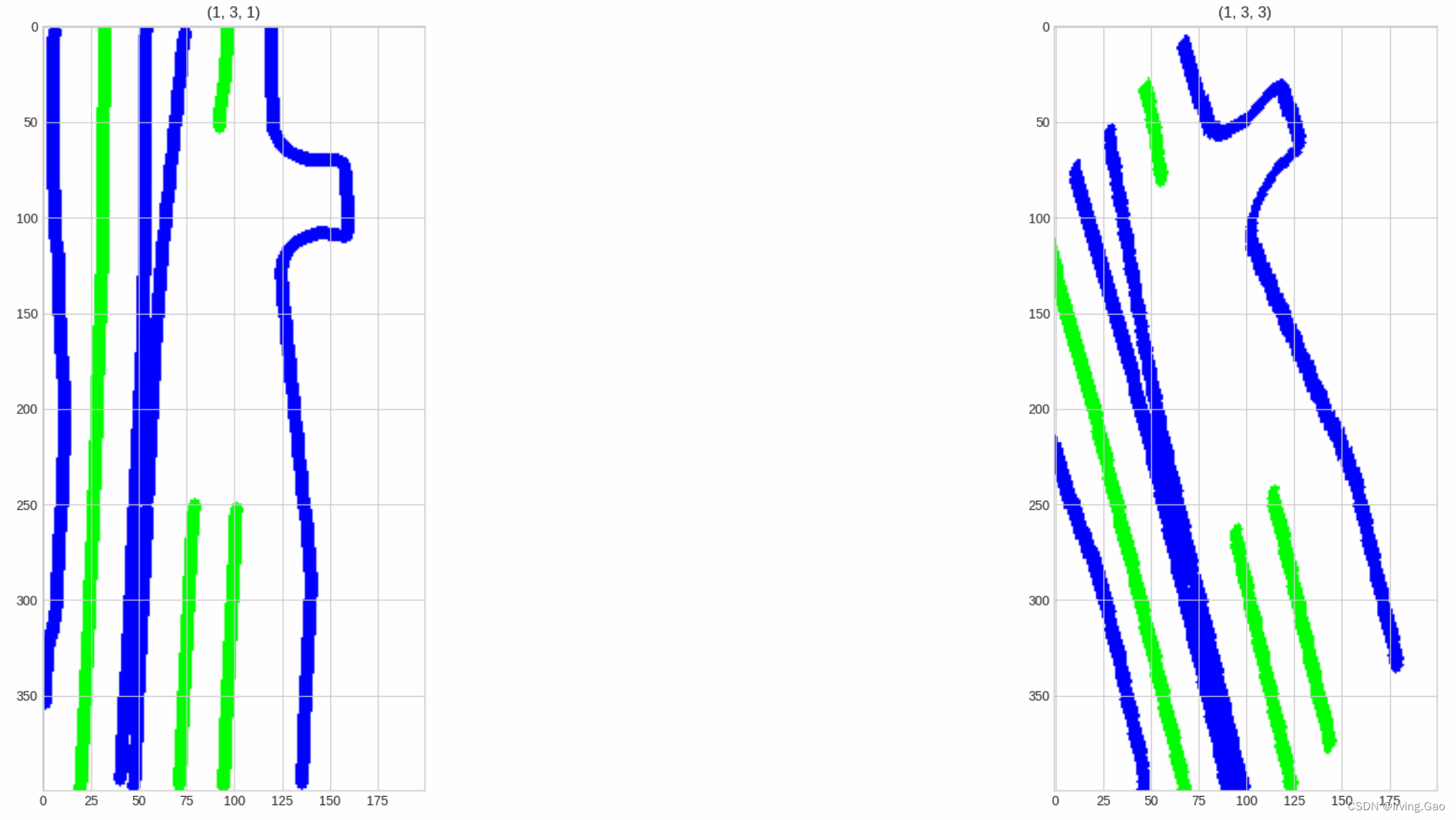
- 旋转效果(左侧为原图,右侧为旋转45°后图像):
矩阵 / 图像 坐标平移
- 这里做平移时有一个非常重要的大坑细节:平移的x和y都是经过归一化的,即在[0-1]之间,务必不要以为是平移的像素个坐标。
shift_x = 0.5
shift_y = 0.5
transform_matrix = torch.tensor([
[1, 0, shift_x],
[0, 1 ,shift_y]]).unsqueeze(0) # 设B(batch size为1)
其他步骤与旋转相同:
grid = F.affine_grid(transform_matrix, # 旋转变换矩阵
src.shape) # 变换后的tensor的shape(与输入tensor相同)
output = F.grid_sample(src, # 输入tensor,shape为[B,C,W,H]
grid, # 上一步输出的gird,shape为[B,C,W,H]
mode='nearest') # 一些图像填充方法,这里我用的是最近邻
# 输出output的shape为[B,C,W,H]
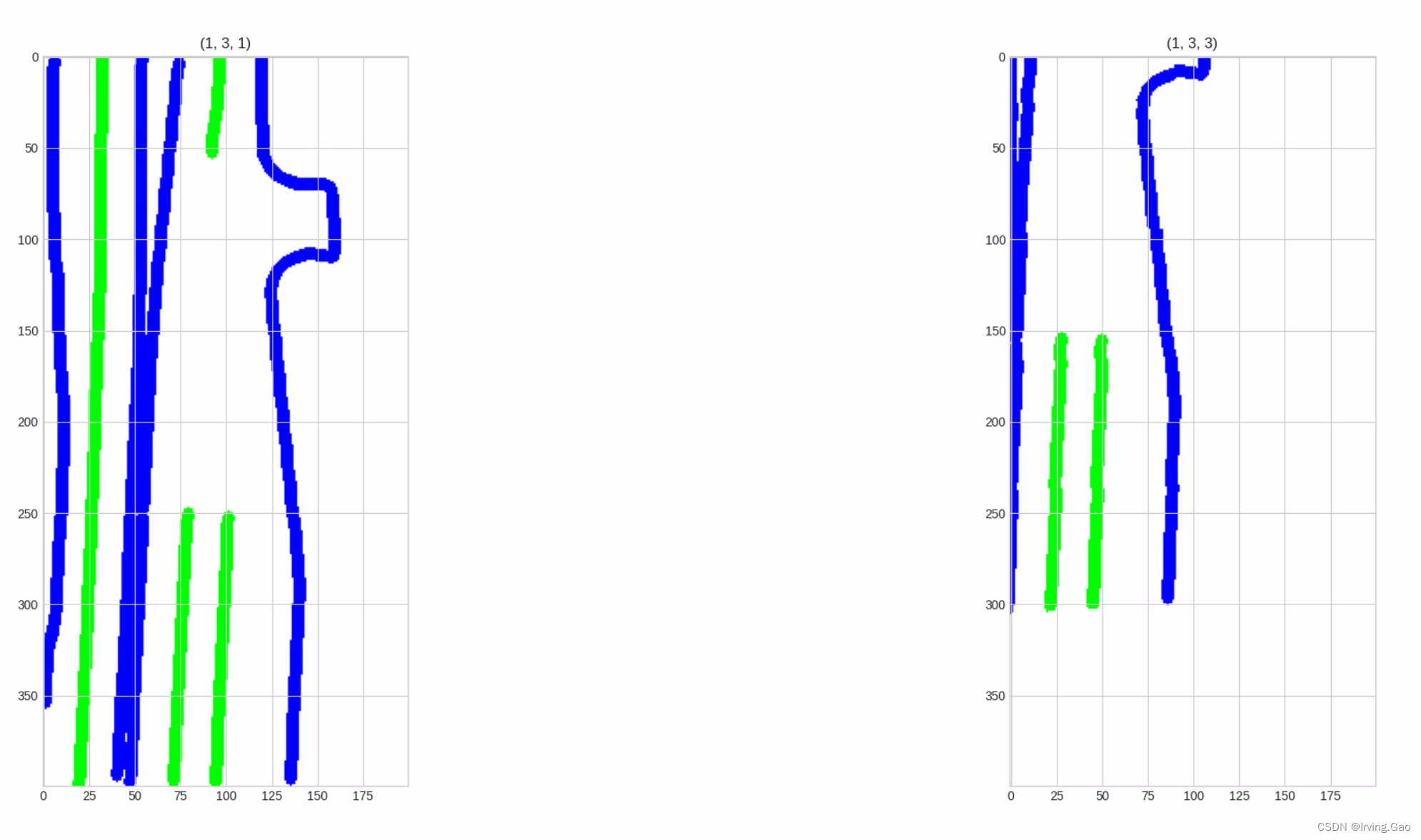
- 平移效果(左侧为原图,右侧为平移后图像):
矩阵 / 图像 坐标平移+旋转
import math
from torch.nn import functional as F
B = 1 # batch size
# 初始化旋转角度和平移量
angle = 45/180*math.pi
shift_x = 0.5
shift_y = 0.5
# 创建一个坐标变换矩阵
transform_matrix = torch.tensor([
[math.cos(angle),math.sin(-angle),shift_x],
[math.sin(angle),math.cos(angle),shift_y]])
# 将坐标变换矩阵的shape从[2,3]转化为[1,2,3],并重复在第0维B次,最终shape为[B,2,3]
transform_matrix = transform_matrix.unsqueeze(0).repeat(B,1,1)
grid = F.affine_grid(transform_matrix, # 旋转变换矩阵
src.shape) # 变换后的tensor的shape(与输入tensor相同)
output = F.grid_sample(src, # 输入tensor,shape为[B,C,W,H]
grid, # 上一步输出的gird,shape为[B,C,W,H]
mode='nearest') # 一些图像填充方法,这里我用的是最近邻
# 输出output的shape为[B,C,W,H]
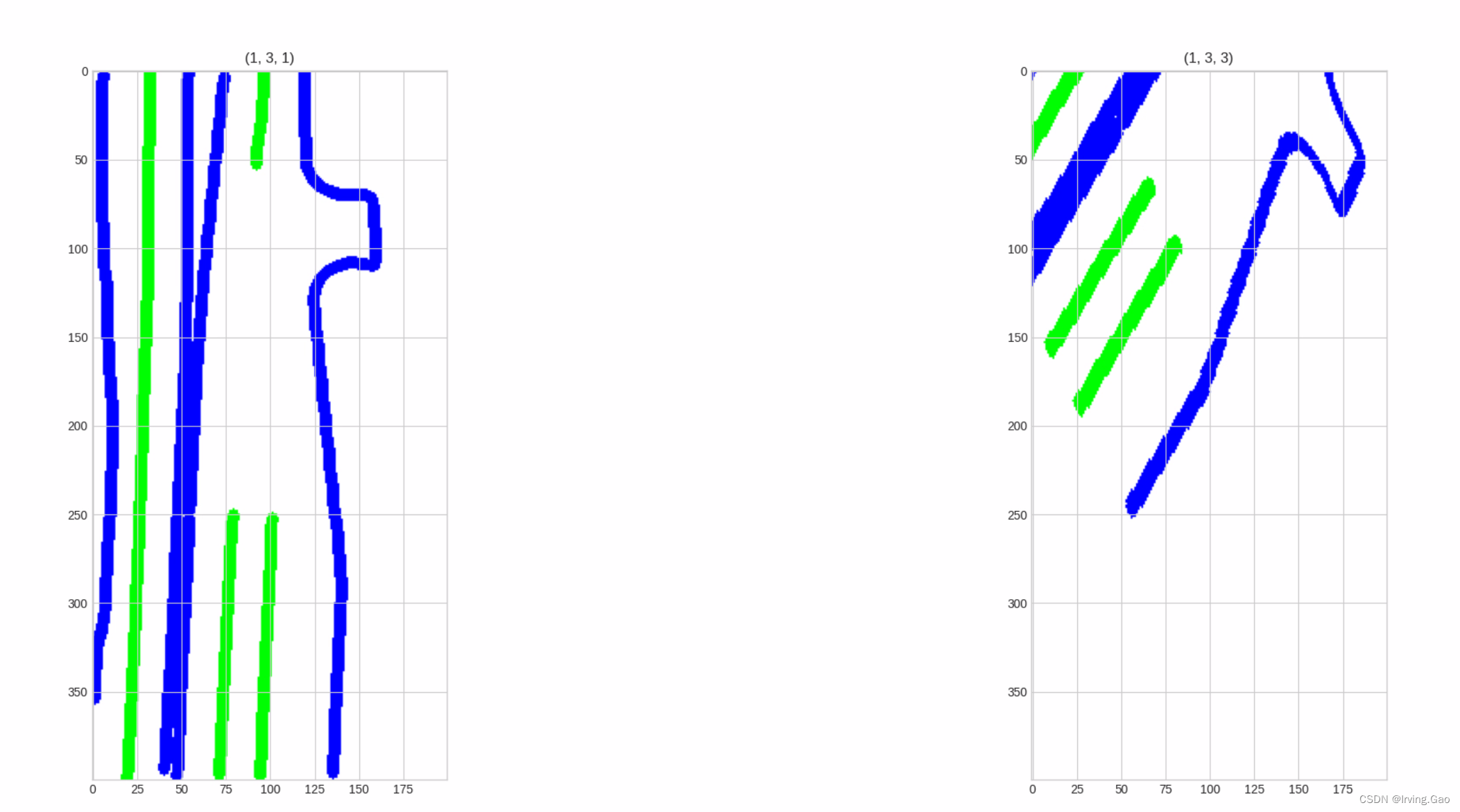
- 平移+旋转效果:
参考文章: