Logistic regression is the go-to linear classification algorithm for two-class problems. It is easy to implement, easy to understand and gets great results on a wide varity of problems, even when the expectation the method has for your data are violated.
After completing this tutorial, you will know:
- How to make predictions with a logistic regression model
- How to estimate coefficients using stochastic gradient descent
- How to apply logistic regression to a real prediction problem.
1.1.1 Logistic Regression
A key difference from linear regression is that the output value being modeled is a binary value (0 or 1) rather than a numeric value.

?yhat prediction is a real value between 0 and 1 that needs to be rounded to an integer value and mapped to a predicted class value. Each column in your input data has an associated b coefficient (a constant real value) that must be learned from your training data. The actual representation of the model that you would store in memory or in a file is the coefficients in the equation (the beta value or b’s). The coefficients of the logistic regression algorithm must be estimated from your training data.
1.1.2 Stochastic Gradient Descent
Logistc Regression uses gradient descent to update the coefficients. Gradient descent was introduced. Each gradient descent iteration, the coefficients (b) in machine learning language are updated using the equation:

1.2 Tutorial
This tutorial is broken down into 3 parts.
- Making Predictions
- Estimating Coefficients
- Pima Indians Diabetes Case Study
This will provide the foundation you need to implement and apply logistic regression with stochastic gradient descent on your own predictive modeling problems.
1.2.1 Making Predictions
The first step is to develop a function that can make predictions. This will be needed both in the evaluation of candidate coefficient values in stochastic gradient descent and after the model is finalized and we wish to start making predictions on test data or new data. Below is a function named predict() that predicts an output value for a row given a set of coefficients. The first coefficient in is always the intercept, also called the bias or b0 as it is standalone and not responsible for a specific input value.
# Make a prediction with coefficients
def predict(row, coefficients):
yhat = coefficients[0]
for i in range(len(row)-1):
yhat += coefficients[i + 1] * row[i]
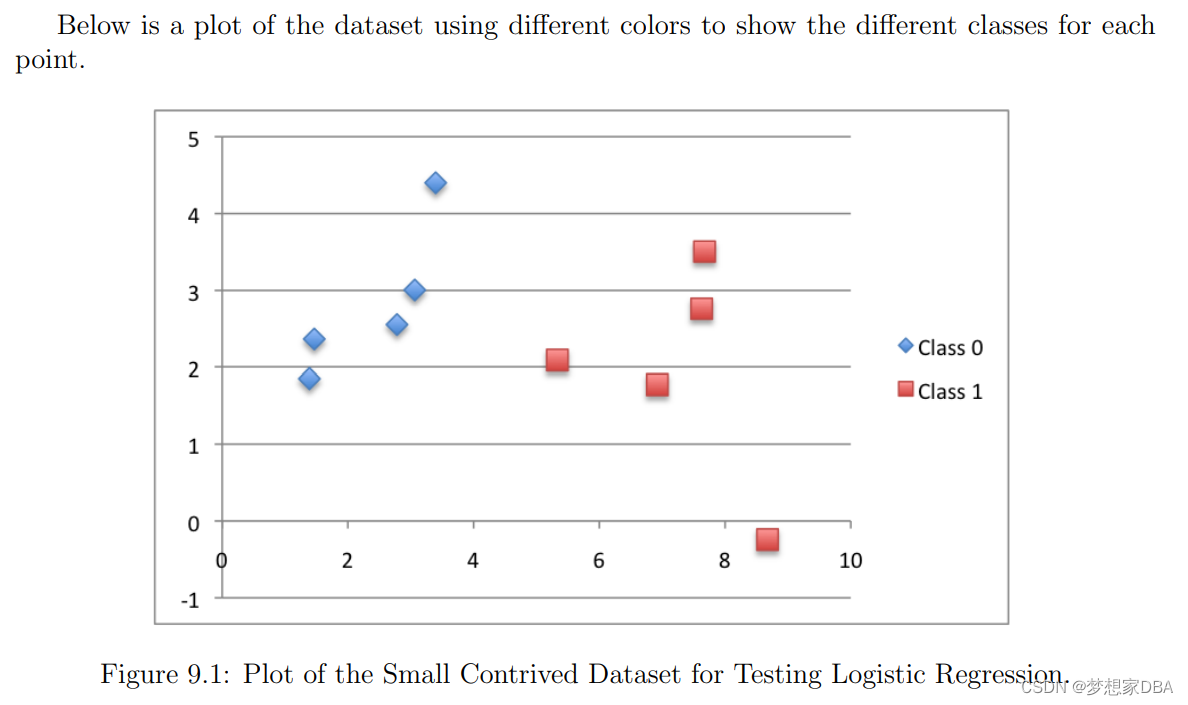
return 1.0 / (1.0 + exp(-yhat))We can contrive a small dataset to test our predict() function.
X1 X2 Y
2.7810836 2.550537003 0
1.465489372 2.362125076 0
3.396561688 4.400293529 0
1.38807019 1.850220317 0
3.06407232 3.005305973 0
7.627531214 2.759262235 1
5.332441248 2.088626775 1
6.922596716 1.77106367 1
8.675418651 -0.242068655 1
7.673756466 3.508563011 1
?
We can also use previously prepared coefficients to make predictions for this dataset. Putting this all together we can test our predict() function below.
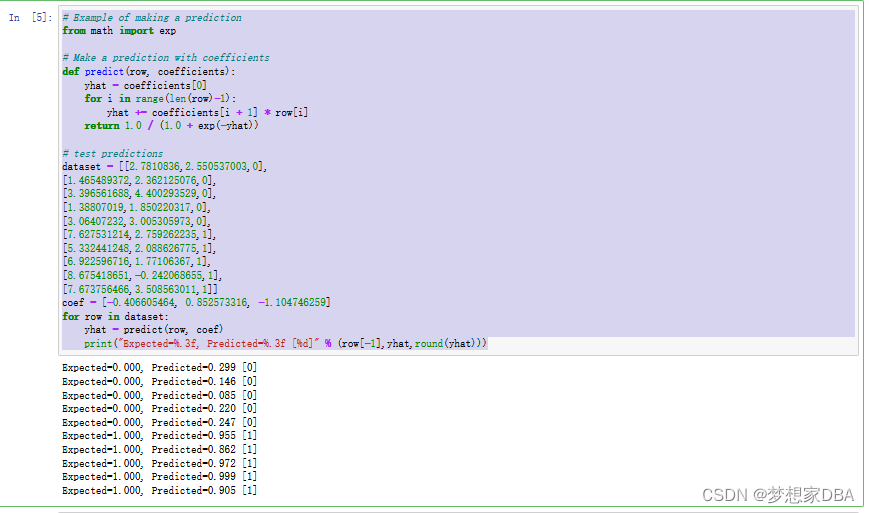
# Example of making a prediction
from math import exp
# Make a prediction with coefficients
def predict(row, coefficients):
yhat = coefficients[0]
for i in range(len(row)-1):
yhat += coefficients[i + 1] * row[i]
return 1.0 / (1.0 + exp(-yhat))
# test predictions
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
coef = [-0.406605464, 0.852573316, -1.104746259]
for row in dataset:
yhat = predict(row, coef)
print("Expected=%.3f, Predicted=%.3f [%d]" % (row[-1],yhat,round(yhat)))
 ?
?
?1.2.2 Estimating Coefficients
We can estimate the coefficient values for our training data using stochastic gradient descent. Stochastic gradient descent requires two parameters:
- Learning Rate: Used to limit the amount each coefficient is corrected each time it is updated.
- Epochs: The number of times to run through the training data while updating the coefficients.

?
# Estimate logistic regressions coefficients using stochastic gradient descent
def coefficients_sgd(train, l_rate, n_epoch):
coef = [0.0 for i in range(len(train[0]))]
for epoch in range(n_epoch):
sum_error = 0
for row in train:
yhat = predict(row, coef)
error = row[-1] - yhat
sum_error += error**2
coef[0] = coef[0] + l_rate * error * yhat * (1.0 - yhat)
for i in range(len(row)-1):
coef[i + 1] = coef[i + 1] + l_rate * error * yhat * (1.0 - yhat) * row[i]
print('>epoch=%d,lrate=%.3f, error=%.3f' %(epoch, l_rate, sum_error))
return coefYou can see that in addition we keep track of the sum of the squared error (a positive value) each epoch so that we can print out a nice message each outer loop. We can test this function on the same small contrived dataset from above.
# Example of estimating coefficients
from math import exp
# Make a prediction with coefficients
def predict(row, coefficients):
yhat = coefficients[0]
for i in range(len(row)-1):
yhat += coefficients[i + 1] * row[i]
return 1.0 / (1.0 + exp(-yhat))
# Estimate logistic regression coefficients using stochastic gradient descent
def coefficients_sgd(train, l_rate, n_epoch):
coef = [0.0 for i in range(len(train[0]))]
for epoch in range(n_epoch):
sum_error = 0
for row in train:
yhat = predict(row, coef)
error = row[-1] - yhat
sum_error += error**2
coef[0] = coef[0] + l_rate * error * yhat * (1.0 - yhat)
for i in range(len(row)-1):
coef[i + 1] = coef[i + 1] + l_rate * error * yhat * (1.0 - yhat) * row[i]
print('>epoch=%d,lrate=%.3f, error=%.3f' %(epoch,l_rate, sum_error))
return coef
# Calculate coefficients
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
l_rate = 0.3
n_epoch = 100
coef = coefficients_sgd(dataset, l_rate, n_epoch)
print(coef)We use a larger learning rate of 0.3 and train the model for 100 epochs, or 100 exposures of the coefficients to the entire training dataset. Running the example prints a message each epoch with the sum squared error for that epoch and the final set of coefficients.
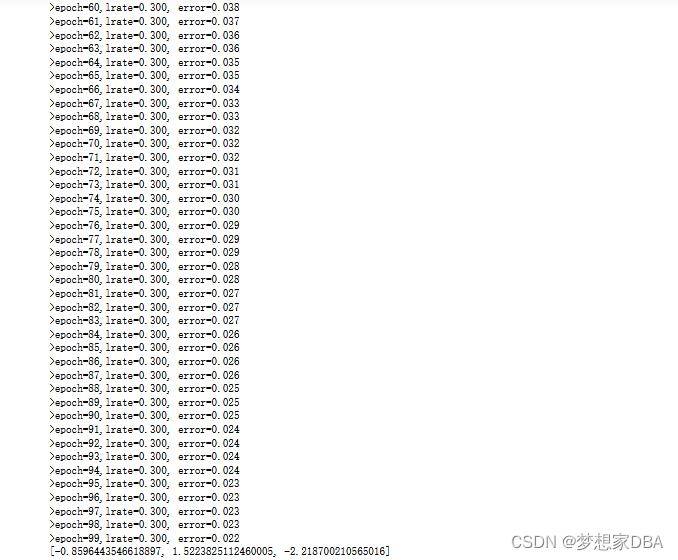
?You can see how error continues to drop even in the final epoch. We could probably train for a lot longer (more epochs) or increase the amount we update the coefficients each epoch (higher learning rate). Experiment and see what you come up with. Now, let’s apply this algorithm on a real dataset.
1.2.3 Pima Indians Diabetes Case Study
We will train a logistic regression model using stochastic gradient descent on the diabetes dataset. The example assumes that a CSV copy of the dataset is in the current working directory with the filename pima-indians-diabetes.csv
?? The dataset is first loaded , the string values converted to numeric and each column is normalized to value in the range of 0 to 1. This is achieved with the helper functions load_csv() and str_column_to_float() to load and prepare the dataset and dataset_minmax() and normalize_dataset() to normalize it.
We will use k-fold cross-validation to estimate the performance of the learned model on unseen data. This means that we will construct and evaluate k models and estimate the performance as the mean model performance. Classification accuracy will be used to evaluate each model. These behaviors are provided in the cross_validation_split(), accuracy_metric() and evaluate_algorithm() helper functions. We will use the predict() and coefficients_sgd() functions created above and a new logistic_regression() function to train the model. Below is the complete example.
# Logistic Regression on Diabetes Dataset
from random import seed
from random import randrange
from csv import reader
from math import exp
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename,'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
for i in range(len(dataset[0])):
col_values = [row[i] for row in dataset]
value_min = min(col_values)
value_max = max(col_values)
minmax.append([value_min, value_max])
return minmax
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)):
row[i] = (row[i] - minmax[i][0])/ (minmax[i][1] - minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set,[])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Make a prediction with coefficients
def predict(row, coefficients):
yhat = coefficients[0]
for i in range(len(row)-1):
yhat += coefficients[i + 1] * row[i]
return 1.0 / (1.0 + exp(-yhat))
# Estimate logistic regression coefficients using stochastic gradient descent
def coefficients_sgd(train, l_rate, n_epoch):
coef = [0.0 for i in range(len(dataset[0]))]
for i in range(n_epoch):
yhat = predict(row,coef)
error = row[-1] - yhat
coef[0] = coef[0] + l_rate * error * yhat * (1.0 - yhat)
for i in range(len(row)-1):
coef[i + 1] = coef[i + 1] * l_rate * error * yhat * (1.0 - yhat) * row[i]
return coef
# logistc Regression Algorithm With Stochastic Gradient Descent
def logistic_regression(train, test, l_rate, n_epoch):
predictions = list()
coef = coefficients_sgd(train, l_rate, n_epoch)
for row in test:
yhat = predict(row, coef)
yhat = round(yhat)
predictions.append(yhat)
return (predictions)
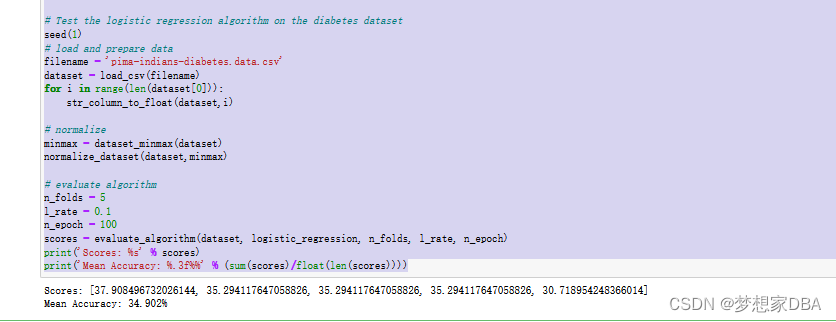
# Test the logistic regression algorithm on the diabetes dataset
seed(1)
# load and prepare data
filename = 'pima-indians-diabetes.data.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])):
str_column_to_float(dataset,i)
# normalize
minmax = dataset_minmax(dataset)
normalize_dataset(dataset,minmax)
# evaluate algorithm
n_folds = 5
l_rate = 0.1
n_epoch = 100
scores = evaluate_algorithm(dataset, logistic_regression, n_folds, l_rate, n_epoch)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))