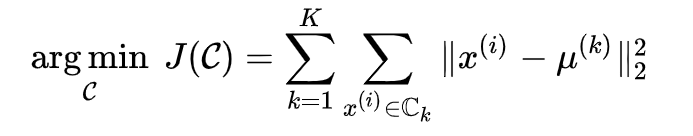[人工智能]K-Mean聚类算法

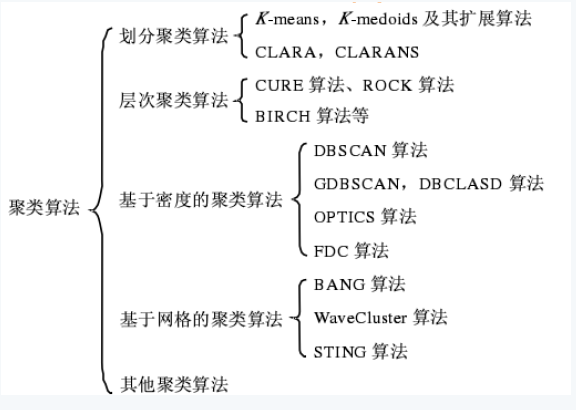
0.前置基础

0.1聚类简介 [3] [5]

**Clustering (聚类)**是常见的unsupervised learning (无监督学习)方法，简单地说就是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集（subset），这样让在同一个子集中的成员对象都有相似的一些属性，常见的包括在坐标系中更加短的空间距离等。聚类的过程，我们并不清楚某一类是什么（通常无标签信息），需要实现的目标只是把相似的样本聚到一起，即只是利用样本数据本身的分布规律。

聚类算法可以大致分为传统聚类算法以及深度聚类算法：

• 传统聚类算法主要是根据原特征+基于划分/密度/层次等方法。

  

• 深度聚类方法主要是根据表征学习后的特征+传统聚类算法。

  

0.2 聚类与分类的区别[4]

聚类与分类算法的最大区别在于, 分类的目标类别已知, 而聚类的目标类别是未知的.[5]

分类：类别是已知的，通过对已知分类的数据进行训练和学习，找到这些不同类的特征，再对未分类的数据进行分类。属于监督学习。

聚类：事先不知道数据会分为几类，通过聚类分析将数据聚合成几个群体。聚类不需要对数据进行训练和学习。属于无监督学习。

1.K-Means算法思想

K-Means聚类算法是一种迭代求解的划分方法聚类分析算法[1] [3]，其主要是来计算数据聚集的算法，主要通过不断地取离种子点最近均值的算法[2]。

简述：k-means即是把 n个点划分到k个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准。[5]

算法思想是：

(版本一)我们需要随机选择K个对象作为初始的聚类中心，然后计算每个对象和各个聚类中心之间的距离，然后将每个对象分配给距离它最近的聚类中心。聚类中心及分配给它们的对象就代表着一个聚类。每分配一个样本，聚类的中心会根据聚类中现有的对象被重新计算。此过程将不断重复，直至满足设置的终止条件。[1]

（版本二）先随机选取K个对象作为初始的聚类中心。然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个：

• 没有（或最小数目）对象被重新分配给不同的聚类。
• 没有（或最小数目）聚类中心再发生变化。
• 误差平方和局部最小。

得到相互分离的球状聚类，在这些聚类中，均值点趋向收敛于聚类中心。 一般会希望得到的聚类大小大致相当，这样把每个观测都分配到离它最近的聚类中心（即均值点）就是比较正确的分配方案。[5]

2.K-Means算法原理及步骤

2.1k-means聚类原理[3]

k-means聚类可以说是聚类算法中最为常见的，它是基于划分方法聚类的，原理是先初始化k个簇类中心，基于计算样本与中心点的距离归纳各簇类下的所属样本，迭代实现样本与其归属的簇类中心的距离为最小的目标。

已知观测集$(x_1,x_2,\dots ,x_n)$，其中每个观测都是一个 d-维实向量，k-平均聚类要把这 n个观测划分到k个集合中(k≤n),使得组内平方和最小。换句话说，它的目标是找到使得下式满足的聚类$S_i$，

其中 ${\mu }_i$ 是$S_i$ 中所有点的均值。[5]

K-means 聚类的迭代算法实际上是 EM 算法，EM 算法解决的是在概率模型中含有无法观测的隐含变量情况下的参数估计问题。

在 K-means 中的隐变量是每个类别所属类别。K-means 算法迭代步骤中的 每次确认中心点以后重新进行标记 对应 EM 算法中的 E 步 求当前参数条件下的 Expectation 。而 根据标记重新求中心点 对应 EM 算法中的 M 步 求似然函数最大化时（损失函数最小时）对应的参数 。EM 算法的缺点是容易陷入局部极小值，这也是 K-means 有时会得到局部最优解的原因。[3]

2.2 k-means计算步骤[1]

K-Means算法的具体步骤如下：

1. 首先我们需要确定一个k值（随机），即我们希望数据经过聚类得到k个不同的集合
2. 从给定的数据集中随机选择K个数据点作为质心
3. 对数据集中的每个点计算其与每一个质心的距离（比如欧式距离）；数据点离哪个质心近，就划分到那个质心所属的集合
4. 第一轮将所有的数据归号集合后，一共有K个集合，然后重新计算每个集合的质心
5. 如果新计算出来的质心和原来的质心之间的距离小于某一个设置的阈值，则表示重新计算的质心的位置变化不大，数据整体趋于稳定，或者说数据已经收敛。在这样的情况下，我们认为聚类效果已经达到了期望的结果，算法可终止。
6. 反之，如果新质心和原来质心的距离变化很大，需要重复迭代3-5步骤，直至位置变化不大，达到收敛状态。

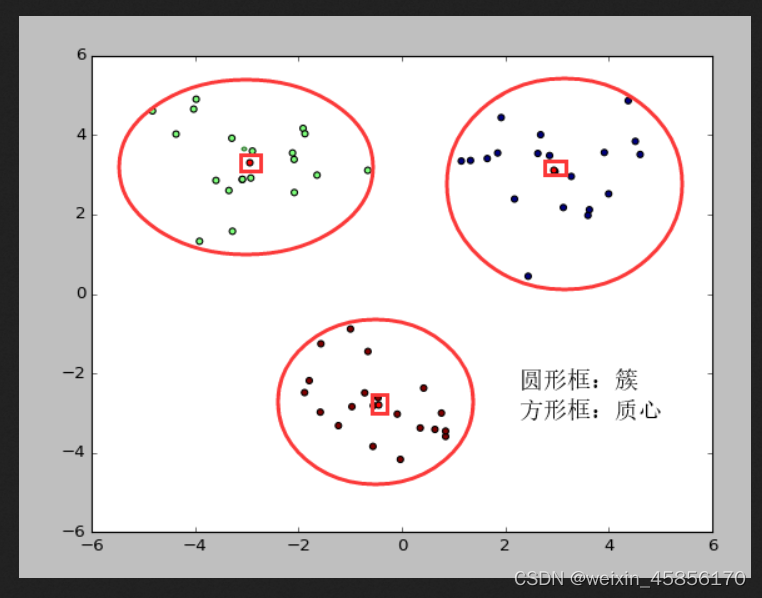
2.3 k-means术语[5]

• 簇: 所有数据的点集合，簇中的对象是相似的。

• 质心: 簇中所有点的中心（计算所有点的均值而来）.

• SSE: Sum of Sqared Error（误差平方和）, 它被用来评估模型的好坏，SSE 值越小，表示越接近它们的质心. 聚类效果越 好。由于对误差取了平方，因此更加注重那些远离中心的点（一般为边界点或离群点）。详情见kmeans的评价标准。
  有关 簇 和 质心 术语更形象的介绍, 请参考下图:

2.4 k-means开发流程[5]

收集数据：使用任意方法
准备数据：需要数值型数据类计算距离, 也可以将标称型数据映射为二值型数据再用于距离计算
分析数据：使用任意方法
训练算法：不适用于无监督学习，即无监督学习不需要训练步骤
测试算法：应用聚类算法、观察结果.可以使用量化的误差指标如误差平方和（后面会介绍）来评价算法的结果.
使用算法：可以用于所希望的任何应用.通常情况下, 簇质心可以代表整个簇的数据来做出决策.

2.5 k-means评价标准[5]

k-means算法因为手动选取k值和初始化随机质心的缘故，每一次的结果不会完全一样，而且由于手动选取k值，我们需要知道我们选取的k值是否合理，聚类效果好不好，那么如何来评价某一次的聚类效果呢？也许将它们画在图上直接观察是最好的办法，但现实是，我们的数据不会仅仅只有两个特征，一般来说都有十几个特征，而观察十几维的空间对我们来说是一个无法完成的任务。

因此，我们需要一个公式来帮助我们判断聚类的性能，这个公式就是SSE (Sum of Squared Error, 误差平方和 ），它其实就是每一个点到其簇内质心的距离的平方值的总和，这个数值对应k-means函数中clusterAssment矩阵的第一列之和。 SSE值越小表示数据点越接近于它们的质心，聚类效果也越好。 因为对误差取了平方，因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数，但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。

2.6 k-means应用场景[5]

k-means，用于数据集内种类属性不明晰，希望能够通过数据挖掘出或自动归类出有相似特点的对象的场景。其商业界的应用场景一般为挖掘出具有相似特点的潜在客户群体以便公司能够重点研究、对症下药。

? 例如，在2000年和2004年的美国总统大选中，候选人的得票数比较接近或者说非常接近。任一候选人得到的普选票数的最大百分比为50.7%而最小百分比为47.9% 如果1%的选民将手中的选票投向另外的候选人，那么选举结果就会截然不同。 实际上，如果妥善加以引导与吸引，少部分选民就会转换立场。尽管这类选举者占的比例较低，但当候选人的选票接近时，这些人的立场无疑会对选举结果产生非常大的影响。如何找出这类选民，以及如何在有限的预算下采取措施来吸引他们？ 答案就是聚类（Clustering)。

? 那么，具体如何实施呢？首先，收集用户的信息，可以同时收集用户满意或不满意的信息，这是因为任何对用户重要的内容都可能影响用户的投票结果。然后，将这些信息输入到某个聚类算法中。接着，对聚类结果中的每一个簇（最好选择最大簇 ）， 精心构造能够吸引该簇选民的消息。最后， 开展竞选活动并观察上述做法是否有效。

? 另一个例子就是产品部门的市场调研了。为了更好的了解自己的用户，产品部门可以采用聚类的方法得到不同特征的用户群体，然后针对不同的用户群体可以对症下药，为他们提供更加精准有效的服务。

3.计算要点

3.1 k值选择[1] [3]

k值决定了我们将数据划分成多少个簇类。k个初始化的质心的位置选择对最后的聚类结果和整个大代码的运行时间都有非常大的影响。因此需要选择合适的k个质心

一般k值是通过先验知识或交叉验证来选取的。K值的确定常用：先验法、手肘法等方法。

1. 先验法
   先验比较简单，就是凭借着业务知识确定k的取值。比如对于iris花数据集，我们大概知道有三种类别，可以按照k=3做聚类验证。从下图可看出，对比聚类预测与实际的iris种类是比较一致的。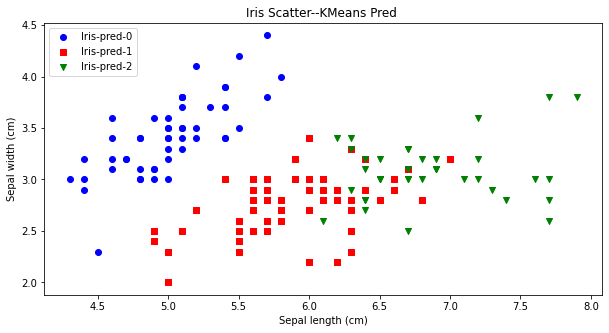

   

   

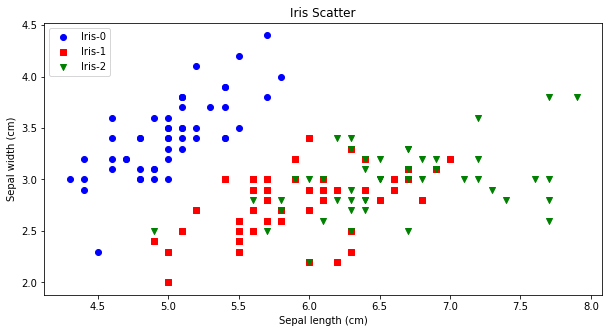
2. 手肘法
   可以知道k值越大，划分的簇群越多，对应的各个点到簇中心的距离的平方的和（类内距离，WSS）越低，我们通过确定WSS随着K的增加而减少的曲线拐点，作为K的取值。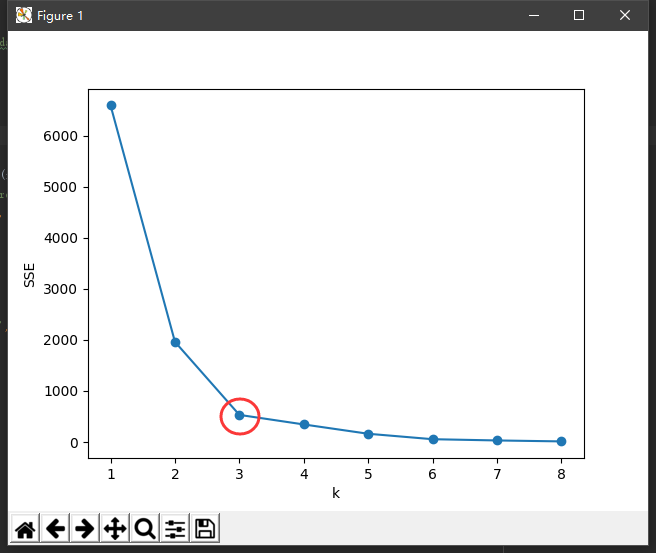

   

手肘法的缺点在于需要人为判断不够自动化，还有些其他方法如：

• 使用 Gap statistic 方法，确定k值。
• 验证不同K值的平均轮廓系数，越趋近1聚类效果越好。
• 验证不同K值的类内距离/类间距离，值越小越好。
• ISODATA算法：它是在k-均值算法的基础上，增加对聚类结果的“合并”和“分裂”两个操作，确定最终的聚类结果。从而不用人为指定k值。

3.2 距离问题

1、两个集合之间的$x_i,x_j$的$L_p$距离定义为：

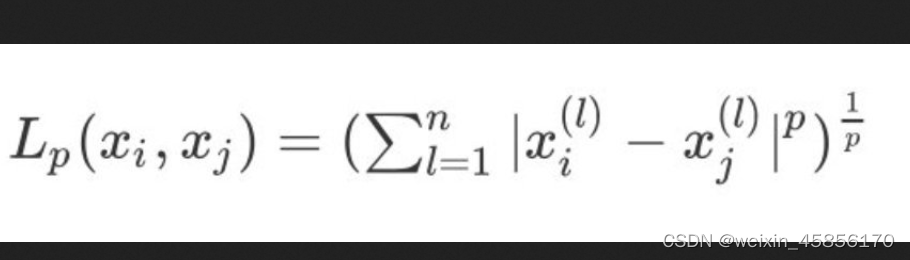
2、当p=1则表示为曼哈顿距离：

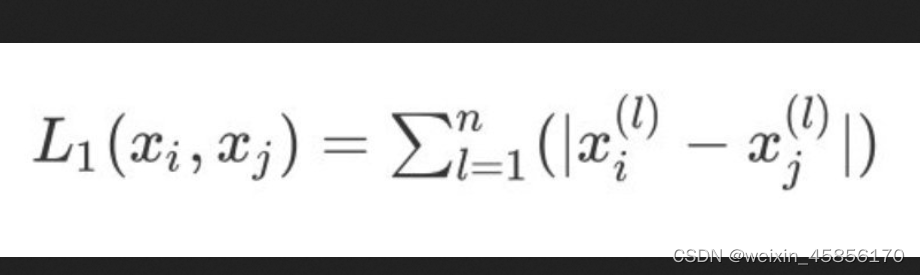
3、当p=2则表示为我们常用的欧式距离：

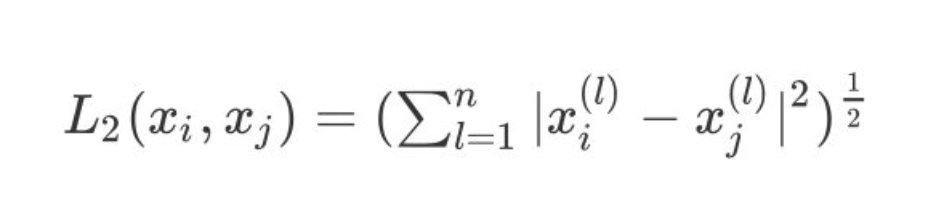
4、当p趋于无穷时，表示为切比雪夫距离，它是各个坐标距离的最大值：

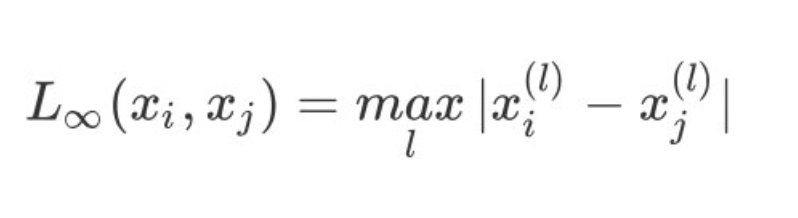
在K-Means算法中一般采用的是欧式距离

4.K-Means优缺点

优点

1. 原理很简单，实现起来也是非常容易，算法收敛速度也很快
2. 聚类效果优，可解释性强。当数据最终收敛之后，我们最终能够很清晰的看到聚类的效果
3. 约束条件少。算法中需要控制的参数只有簇数k。通过对k的不断调节才能得到最好的聚类效果

缺点

1. k值的选取不好把握，很多情况下K值的估计是非常困难的，有时候通过交叉验证来获取。
2. 迭代的方法得到的结果只能是局部最优解，而不能得到全局最优解。
3. 对噪音和异常点很敏感。异常点对质心的确定影响很大的。可以用来检测异常值。(K-means++算法改进点)
4. K-Means算法需要用初始随机种子点来搞，这个随机种子点太重要，不同的随机种子点会有得到完全不同的结果。[2]

5.python实现K-means[1]

import numpy as np
import pandas as pd
import random  # 随机模块
import re
import matplotlib.pyplot as plt


# 导入数据
def loadDataSet():
  dataset = np.loadtext("user/skl/cluster/dataset.csv")  # 个人文件路径
  return dataset   # 返回数据集

# 绘图函数
def show_fig():
  dataset = loadDataSet()   # 导入数据
  fig = plt.figure()  # 确定画布
  ax = fig.add_subplot(111)   # 一个子图
  ax.scatter(dataset[:,0], dataset[:,1])  # 传入绘图数据
  plt.show()
  
# 定义欧式距离公式
# 两个向量间的欧式距离公式：[(x_1 - x_2)^2 + (y_1 - y_2)^2 + (x_n - y_n)^2]
def calcudistance(vec1,vec2):  # 传入两个向量
  return np.sqrt(np.sum(np.square(vec1 - vec2)))  # 向量相减在平方，最后再求和
  
# 初始化质心
def initCentroids(dataset, k):
  # 初始化执行；dataset是传入的数据
  # k：选择分类簇的个数
  dataset = list(dataset)  # 数据列表化
  return random.sample(dataset,k)   # 随机选取k的模块

# 计算每个数据点和质心的距离，并归属到距离最小的类别中
def minDisctance(dataset, centroidList):  # 传入数据集和选取的质心列表
  clusterDict = dict()  # 保存簇类结果
  k = len(centroidList)  # 质心列表的长度：总共多少个质心表示分成多少类
  for item in dataset:  # 原始数据中的每个元素
    vec1 = item  # 数据中的向量
    flag = -1  # 标志位
    minDis = float("inf")   # 初始化为无穷大值
    for i in range(k):
      vec2 = centroidList[i]   # 取出第i个质心
      distcance = calcudistance(vec1, vec2)   # 计算欧式距离
      if distance < minDis:   
        minDis = distance  # 如果算出来的实际距离小于最小值的初始值，则将真实值distance赋值给最小值（更新最小值）
        flag = i  # 循环结束时，flag保存与当前item最近的簇标记
    if flag not in clusterDict.keys():
      clusterDict.setdefault(flag,[])
    clusterDict[flag].append(item)  # 加入到相应的簇类中
  return clusterDict  # 不同的类别

# 重新计算质心
def getcentroids(clusterDict):
  # 重新计算k个质心
  centroidList = []   # 质心空列表
  for key in clusterDict.keys():  # 
    centroid = np.mean(clusterDict[key], axis=0)  # 现有数据点的平均值
    centroidList.append(centroid)
  return centroidList  # 得到新的质心
    
# 计算均方误差
def getVar(centroidList, clusterDict):
  # 将簇类中各个向量和质心的距离累加求和
  sum = 0.0  # 初始值
  for key in clusterDict.keys():   # 簇类中的键
    vec1 = centroidList[key]   # 取出某个质心
    distance = 0.0  # 距离初始化值
    for item in clusterDict[key]:  # 簇类的键
      vec2 = item
      distance += calcudistance(vec1, vec2)  # 求距离
    sum += distance  # 累加
  return sum

# 显示簇类
def showCluster(centroidList, clusterDict):
  # 显示簇类结果
  color_mark = ["or","ob","og","ok","oy","ow"]
  centroid_mark = ["dr","db","dg","dk","dy","dw"]
  
  for key in clusterDict.keys():
    plt.plot(centroidList[key][0], centroidList[key][1], centroidMark[key],markersize=12)  # 质心点
    for item in clusterDict[key]:
      plt.plot(item[0],item[1],colorMark[key])
  plt.show()
  
# 主函数
def main():
  dataset = loadDataSet()  # 导入数据
  centroidList = initCentroids(dataset,4)   # 质心列表
  clusterDict = minDistance(dataset, centroidList)   # 簇类的字典数据
  newVar = getVar(centroidList, clusterDict)   # 质心和簇类中数据得到新的误差
  oldVar = 1  # 当两次聚类的误差小于某个值时，说明质心基本稳定
  
  times = 2
  while abs(newVar - oldVar) >= 0.00001:   # 当新旧误差的绝对值小于某个很小的值
    centroidList = getCentroids(clusterDict)   # 得到质心列表
    oldVar = newVar  # 将新的误差赋值给旧误差
    newVar = getVar(centroidList, clusterDict)   # 新误差
    times += 1
    showCluster(centroidList, clusterDict)  # 显示聚类结果
    
    
if __name__ == "__main__":
  show_fig()
  main()

6.调用机器学习库sklearn实现k-means 聚类[5]

import numpy as np
import matplotlib.pyplot as plt

from sklearn.cluster import KMeans

# 加载数据集
dataMat = []
fr = open(“./testSet2.txt”) # 注意，这个是相对路径
for line in fr.readlines():
curLine = line.strip().split(‘\t’)
fltLine = list(map(float,curLine)) # 映射所有的元素为 float（浮点数）类型
dataMat.append(fltLine)

# 训练k-means算法模型
km = KMeans(n_clusters=3) # 初始化
km.fit(dataMat) # 拟合
km_pred = km.predict(dataMat) # 预测
centers = km.cluster_centers_ # 质心

# 可视化结果
plt.scatter(np.array(dataMat)[:, 1], np.array(dataMat)[:, 0], c=km_pred)
plt.scatter(centers[:, 1], centers[:, 0], c="r")
plt.show()

7.延展学习

传统的K-Means算法存在一些缺陷，比如K值的选取不是很好把握、对异常数据敏感等，于是提出了很多在其基础上改进的聚类算法：

7.1、K-Means++（初始化优化）

针对K-Means算法中随机初始化质心的方法进行了优化。

优化的思路是：各个簇类中心应该互相离得越远越好。基于各点到已有中心点的距离分量，依次随机选取到k个元素作为中心点。离已确定的簇中心点的距离越远，越有可能（可能性正比与距离的平方）被选择作为另一个簇的中心点。

过程：[6]

? a) 从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1μ1
　b) 对于数据集中的每一个点xixi，计算它与已选择的聚类中心中最近聚类中心的距离$D(x_i)=argmin||xi?\mu r|{|}_2^{2}r=1,2,...k_{selected}$

c) 选择一个新的数据点作为新的聚类中心，选择的原则是：$D(x)$较大的点，被选取作为聚类中心的概率较大
　d) 重复b和c直到选择出k个聚类质心
　e) 利用这k个质心来作为初始化质心去运行标准的K-Means算法

如下代码。[3]

# Kmeans ++ 算法基于距离概率选择k个中心点
            # 1.随机选择一个点
            center = []
            center.append(random.choice(range(len(self.data[0]))))
            # 2.根据距离的概率选择其他中心点
            for i in range(self.k - 1):
                weights = [self.distance_closest(self.data[0][x], center) 
                         for x in range(len(self.data[0])) if x not in center]
                dp = [x for x in range(len(self.data[0])) if x not in center]
                total = sum(weights)
                #基于距离设定权重
                weights = [weight/total for weight in weights]
                num = random.random()
                x = -1
                i = 0
                while i < num :
                    x += 1
                    i += weights[x]
                center.append(dp[x])
            center = [self.data_dict[self.data[0][center[k]]] for k in range(len(center))]

7.2、elkan K-Means（距离优化）

在传统的K-Means算法中，在每轮迭代中我们都需要计算所有的样本点到质心的距离，这样是非常耗时的。

elkan K-Means算法利用：两边之和大于等于第三边，以及两边之差小于第三边的三角形性质，来减少距离的计算。

? 第一种规律是对于一个样本点$x$和两个质心${\mu }_{j1},{\mu }_{j2}$。如果我们预先计算出了这两个质心之间的距离$D(j_1,j_2)$，则如果计算发现$2D(x,j_1)\le D(j_1,j_2)$,我们立即就可以知道$D(x,j_1)\le D(x,j_2)$。此时我们不需要再计算$D(x,j_2)$,也就是说省了一步距离计算。[6]

第二种规律是对于一个样本点xx和两个质心${\mu }_{j1},{\mu }_{j2}$。我们可以得到$D(x,j_2)\ge max0,D(x,j_1)?D(j_1,j_2)$。这个从三角形的性质也很容易得到。[6]

利用上边的两个规律，elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本的特征是稀疏的，有缺失值的话，这个方法就不使用了，此时某些距离无法计算，则不能使用该算法。[6]

7.3、Mini Batch K-Means算法（大样本优化）

在传统的K-Means算法中，要计算所有的样本点到所有的质心的距离。现在大数据时代，如果样本量非常大，传统的算法将会非常耗时。

Mini Batch K-Means就是从原始的样本集中随机选择一部分样本做传统的K-Means。这样可以避免样本量太大的计算难题，同时也加速算法的收敛。当然，此时的代价就是我们最终聚类的精度会降低一些。

为了增加算法的准确性，我们一般会多跑几次Mini Batch K-Means算法，用得到不同的随机样本集来得到聚类簇，选择其中最优的聚类簇。

7.4、核K-means [3]

基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布，但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化，这时算法又称为核 K-means 算法，是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射，将输入空间中的数据点映射到高位的特征空间中，并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率，从而在经典的聚类算法失效的情况下，通过引入核函数可以达到更为准确的聚类结果。

8.参考文档

主要参考：[1] 图解K-Means算法

补充参考：

[2] 机器学习之K均值算法（K-means）聚类

[3] 【机器学习】全面解析Kmeans聚类算法（Python）

[4] 5 分钟带你弄懂 k-means 聚类

[5] 一步步教你轻松学K-means聚类算法

[6] [K-Means聚类算法原理 ]