线性模型
1.基本形式
线性模型是通过属性的线性组合来进行预测的函数,形式如下
f
(
x
)
=
w
1
x
1
+
w
2
x
2
+
?
+
w
i
x
i
+
b
f(x)=w_1 x_1+w_2 x_2+?+w_i x_i+b
f(x)=w1?x1?+w2?x2?+?+wi?xi?+b
简化写成向量形式:
f
(
x
)
=
w
T
x
+
b
f(x) = w^Tx + b
f(x)=wTx+b---------------------------------------------------------------------------------(1)
其中
w
w
w = (
w
1
,
w
2
.
.
.
;
w
i
w_1,w_2...;w_i
w1?,w2?...;wi?).这里
w
和
b
w和b
w和b学得之后就可以确定模型。
2.线性回归
将属性转化为数值:对离散属性,若属性值间存在“序”关系,则转化为连续值,例如:二值属性“胖瘦”的取值“胖” “瘦可转化为{1.0,0.0}
非连续属性值可以转化为k维向量。
2.1均方误差最小化
f
(
x
i
)
=
w
T
x
i
+
b
f(x_i) = w^Tx_i + b
f(xi?)=wTxi?+b,要使预测值
f
(
x
i
)
?
y
i
f(x_i) \simeq y_i
f(xi?)?yi? ,需要确定
w
,
b
w,b
w,b的取值,使得所有样本到直线上的直线距离之和最小,这里就要用到均方误差最小化来求解。
E
(
w
,
b
)
=
Σ
i
m
(
y
i
?
w
x
i
?
b
)
2
E(w,b) = \Sigma_i^m(y_i - wx_i - b)^2
E(w,b)=Σim?(yi??wxi??b)2i从1开始
2.2证明凸函数
凸集:若两个点属于同一个集合,则这两点连线上的任意一点都属于此集合。
凸函数:设D是非空凸集,
f
f
f是定义在D上的函数,如果对于任意的
x
1
,
x
2
∈
D
,
α
∈
(
0
,
1
)
x_1,x_2\in D,\alpha\in(0,1)
x1?,x2?∈D,α∈(0,1),均有
f
(
α
x
1
+
(
1
?
α
)
x
2
)
≤
α
f
(
x
1
)
+
(
1
?
α
)
f
(
x
2
)
f(\alpha x_1 + (1-\alpha) x_2) \le\alpha f(x_1) + (1-\alpha)f(x_2)
f(αx1?+(1?α)x2?)≤αf(x1?)+(1?α)f(x2?)
则称为
f
f
f为
D
D
D上的凸函数。
注意:这里说的凸函数和高数中的凸函数不一样。
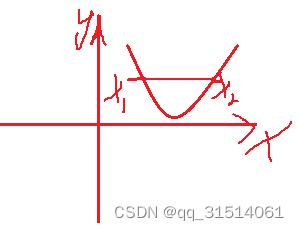
证明
E
(
w
,
b
)
E(w,b)
E(w,b)是关于
w
和
b
w和b
w和b的凸函数,就是证明各分量二阶偏导数
?
2
f
(
x
)
?
x
i
?
x
j
\frac{\partial^2f(x)}{\partial x_i\partial x_j}
?xi??xj??2f(x)?都存在。
2.3用凸函数求最值求解 w , b w,b w,b
2.4 极大似然估计求最大值等价于求均方差最小值
3.对数几率回归
在线性模型的基础上套一个映射函数,来实现分类功能。
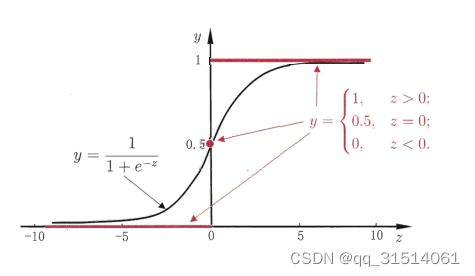
映射函数为对数几率函数:
y
=
1
1
+
e
?
z
y = \frac{1}{1+e^-z}
y=1+e?z1?
然后用极大似然对数来估计
w
和
b
w和b
w和b,
l
(
β
)
=
Σ
i
=
1
m
l
n
p
(
y
i
∣
x
i
;
w
,
b
)
,
l(\beta) = \Sigma^{m}_{i=1}lnp(y_i|x_i;w,b),
l(β)=Σi=1m?lnp(yi?∣xi?;w,b),
对数几率回归算法的机器学习三要素:
1.模型:线性模型输出值为【0,1】,近似阶跃函数,单调可微
2.策略:极大释然估计
3.算法:梯度下降法
4.线性判别分析
算法原理:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点足够近,异类的样例的投影点足够远
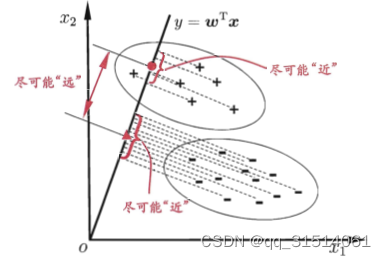
损失函数:
?
J
=
∣
∣
w
T
μ
0
?
w
T
μ
1
∣
∣
2
2
w
T
(
∑
0
+
∑
1
)
w
\ J = \frac{||w^T\mu_0-w^T\mu_1||_2^2}{w^T({\sum}_0+{\sum}_1)w}
?J=wT(∑0?+∑1?)w∣∣wTμ0??wTμ1?∣∣22?? 。
其
中
∣
∣
2
其中||_2
其中∣∣2? 表示二范数:向量的模长
=
w
T
(
μ
0
?
μ
1
)
T
(
μ
0
?
μ
1
)
w
w
T
(
∑
0
+
∑
1
)
w
= \frac{w^T(\mu_0-\mu_1)^T(\mu_0-\mu_1)w}{w^T({\sum}_0+{\sum}_1)w}
=wT(∑0?+∑1?)wwT(μ0??μ1?)T(μ0??μ1?)w?
可将上式重写为:
max
?
J
=
w
T
S
b
w
w
T
S
w
w
\max J = \frac{w^TS_bw}{w^TS_ww}
maxJ=wTSw?wwTSb?w?
S
w
矩
阵
是
固
定
的
,
w
模
长
不
影
响
上
式
S_w 矩阵是固定的,w模长不影响上式
Sw?矩阵是固定的,w模长不影响上式
令
w
T
S
w
w
=
1
w^TS_ww = 1
wTSw?w=1
把上式转为最小化问题
min
?
?
w
T
S
b
w
\min -w^TS_bw
min?wTSb?w最小时原式最大