1. 前言

《MATLAB 神经网络43个案例分析》是MATLAB技术论坛（www.matlabsky.com）策划，由王小川老师主导，2013年北京航空航天大学出版社出版的关于MATLAB为工具的一本MATLAB实例教学书籍，是在《MATLAB神经网络30个案例分析》的基础上修改、补充而成的，秉承着“理论讲解—案例分析—应用扩展”这一特色，帮助读者更加直观、生动地学习神经网络。

《MATLAB神经网络43个案例分析》共有43章，内容涵盖常见的神经网络（BP、RBF、SOM、Hopfield、Elman、LVQ、Kohonen、GRNN、NARX等）以及相关智能算法（SVM、决策树、随机森林、极限学习机等）。同时，部分章节也涉及了常见的优化算法（遗传算法、蚁群算法等）与神经网络的结合问题。此外，《MATLAB神经网络43个案例分析》还介绍了MATLAB R2012b中神经网络工具箱的新增功能与特性，如神经网络并行计算、定制神经网络、神经网络高效编程等。

近年来随着人工智能研究的兴起，神经网络这个相关方向也迎来了又一阵研究热潮，由于其在信号处理领域中的不俗表现，神经网络方法也在不断深入应用到语音和图像方向的各种应用当中，本文结合书中案例，对其进行仿真实现，也算是进行一次重新学习，希望可以温故知新，加强并提升自己对神经网络这一方法在各领域中应用的理解与实践。自己正好在多抓鱼上入手了这本书，下面开始进行仿真示例，主要以介绍各章节中源码应用示例为主，本文主要基于MATLAB2015b(32位)平台仿真实现，这是本书第二十章LIBSVM-FarutoUltimate工具箱及GUI版本介绍与使用实例，话不多说，开始！

2. MATLAB 仿真示例

打开MATLAB，点击“主页”，点击“打开”，找到示例文件
在这里插入图片描述
选中TutorialTest.m，点击“打开”

TutorialTest.m源码如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能：LIBSVM-FarutoUltimate工具箱及GUI版本介绍与使用
%环境：Win7，Matlab2015b
%Modi: C.S
%时间：2022-06-17
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%% TutorialTest

%% Matlab神经网络43个案例分析

% LIBSVM-FarutoUltimate工具箱及GUI版本介绍与使用
% by 李洋(faruto)
% http://www.matlabsky.com
% Email:faruto@163.com
% http://weibo.com/faruto 
% http://blog.sina.com.cn/faruto
% 2013.01.01
%% 若转载请注明：
% faruto and liyang , LIBSVM-farutoUltimateVersion 
% a toolbox with implements for support vector machines based on libsvm, 2011. 
% Software available at http://www.matlabsky.com
% 
% Chih-Chung Chang and Chih-Jen Lin, LIBSVM : a library for
% support vector machines, 2001. Software available at
% http://www.csie.ntu.edu.tw/~cjlin/libsvm
%%
tic;
close all;
clear;
clc;
format compact;
%% test for scaleForSVM
train_data = [1 12;3 4;7 8]
test_data = [9 10;6 2]

[train_scale,test_scale,ps] = scaleForSVM(train_data,test_data,0,1)

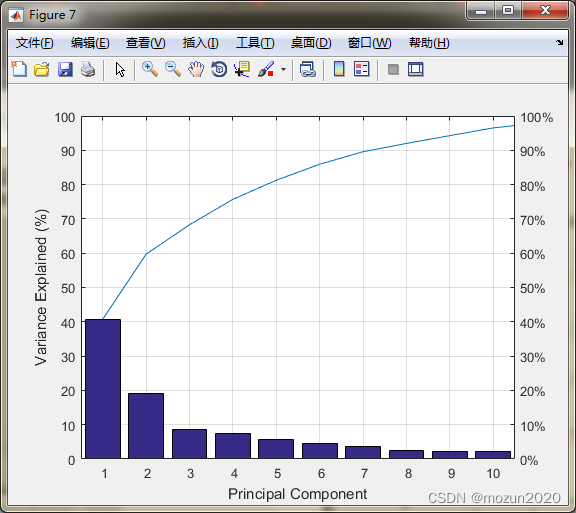
%% test for pcaForSVM
load wine_test
whos train_data
[train_scale,test_scale,ps] = scaleForSVM(train_data,test_data,0,1);
[train_pca,test_pca] = pcaForSVM(train_scale,test_scale,95);
whos train_pca

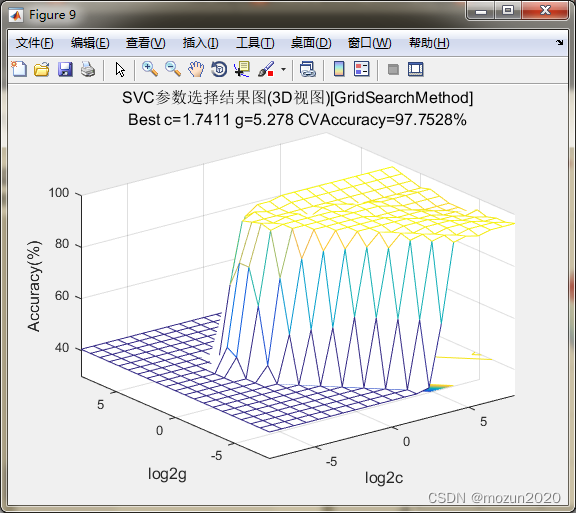
%% test for SVMcgForClass
load wine_test
[train_scale,test_scale,ps] = scaleForSVM(train_data,test_data,0,1);
[bestacc,bestc,bestg]=SVMcgForClass(train_data_labels,train_scale,-10,10,-10,10,5,0.5,0.5,4.5)

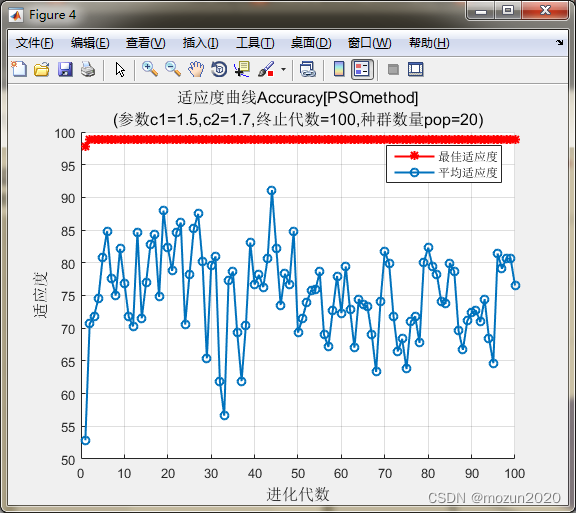
%% test for psoSVMcgForClass
load wine_test
[train_scale,test_scale,ps] = scaleForSVM(train_data,test_data,0,1);

    pso_option.c1 = 1.5;
    pso_option.c2 = 1.7;
    pso_option.maxgen = 100;
    pso_option.sizepop = 20;
    pso_option.k = 0.6;
    pso_option.wV = 1;
    pso_option.wP = 1;
    pso_option.v = 5;
    pso_option.popcmax = 100;
    pso_option.popcmin = 0.1;
    pso_option.popgmax = 100;
    pso_option.popgmin = 0.1;
    
[bestacc,bestc,bestg]=psoSVMcgForClass(train_data_labels,train_scale,pso_option)
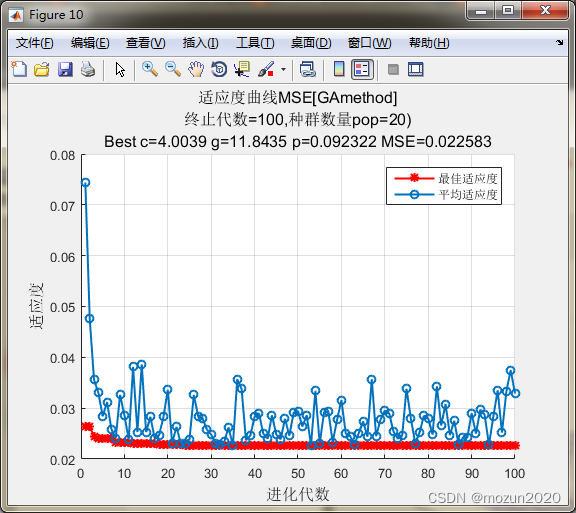
%% test for gaSVMcgForClass
load wine_test
[train_scale,test_scale,ps] = scaleForSVM(train_data,test_data,0,1);
    ga_option.maxgen = 100;
    ga_option.sizepop = 20;
    ga_option.cbound = [0,100];
    ga_option.gbound = [0,100];
    ga_option.v = 10;
    ga_option.ggap = 0.9;
[bestacc,bestc,bestg]=gaSVMcgForClass(train_data_labels,train_scale,ga_option)
%% test for svmplot
load fisheriris;
data = [meas(:,1), meas(:,2)];
groups = ismember(species,'setosa');
[train, test] = crossvalind('holdOut',groups);
dataset = data(train,:);
labels = double(groups(train));
model = svmtrain(labels,dataset,'-c 2 -g 0.1');
svmplot(labels,dataset,model);
%% test for SVC.m
load wine_test;
train_label = train_data_labels;
train_data = train_data;
test_label = test_data_labels;
test_data = test_data;

Method_option.plotOriginal = 0;
Method_option.scale = 1;
Method_option.plotScale = 0;
Method_option.pca = 1;
Method_option.type = 1;

[predict_label,accuracy] = SVC(train_label,train_data,test_label,test_data,Method_option);
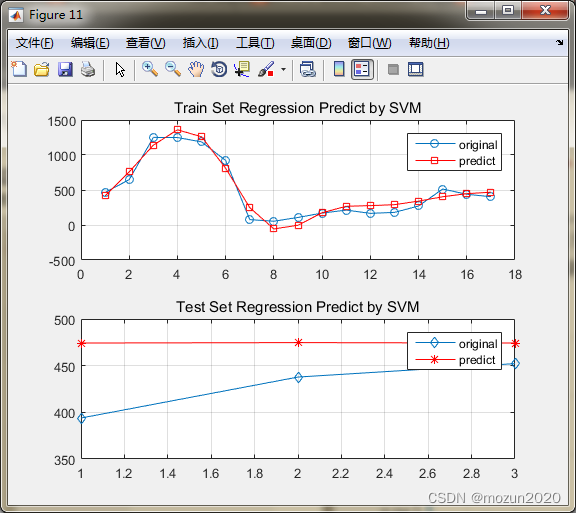
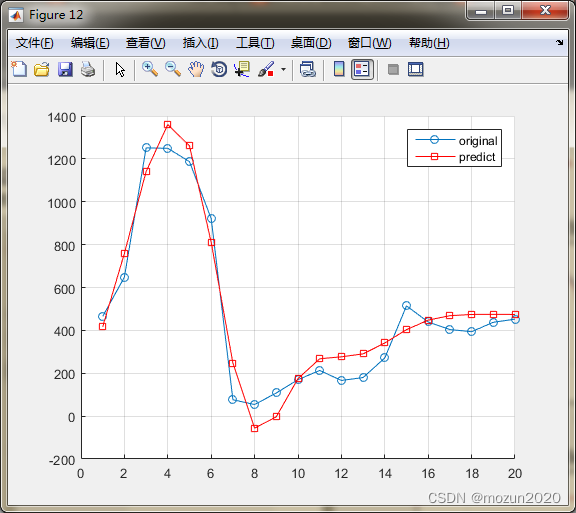
%% test for SVR.m
load x123;
train_y = x1(1:17);
train_x = [1:17]';
test_y = x1(18:end,:);
test_x = [18:20]';

Method_option.plotOriginal = 0;
Method_option.xscale = 1;
Method_option.yscale = 1;
Method_option.plotScale = 0;
Method_option.pca = 0;
Method_option.type = 5;

[predict_Y,mse,r] = SVR(train_y,train_x,test_y,test_x,Method_option);
%% test for VF.m
load wine_test
[train_scale,test_scale,ps] = scaleForSVM(train_data,test_data,0,1);
model = svmtrain(train_data_labels,train_scale,'-c 2 -g 0.1');
[pre,acc] = svmpredict(train_data_labels,train_scale,model);
[score,str] = VF(train_data_labels,pre,1)
[score,str] = VF(train_data_labels,pre,2)
[score,str] = VF(train_data_labels,pre,3)
[score,str] = VF(train_data_labels,pre,4)
[score,str] = VF(train_data_labels,pre,5)
%% test for ClassResult.m
load heart_scale.mat;
data = heart_scale_inst;
label = heart_scale_label;
model = svmtrain(label,data);
type = 1;
CR = ClassResult(label, data, model, type)
%% test for plotSVMroc
load wine_test
[train_data,test_data] = scaleForSVM(train_data,test_data,0,1); 
model = svmtrain(train_data_labels,train_data,'-c 0.01 -g 0.01 -b 1');
[pre,acc,dec] = svmpredict(train_data_labels,train_data,model,'-b 1');
plotSVMroc(train_data_labels,dec,3)
%%
toc;

添加完毕，点击“运行”，开始仿真，输出仿真结果如下：

train_data =
     1    12
     3     4
     7     8
test_data =
     9    10
     6     2
train_scale =
         0    1.0000
    0.2500    0.2000
    0.7500    0.6000
test_scale =
    1.0000    0.8000
    0.6250         0
ps = 
         name: 'mapminmax'
        xrows: 2
         xmax: [2x1 double]
         xmin: [2x1 double]
       xrange: [2x1 double]
        yrows: 2
         ymax: 1
         ymin: 0
       yrange: 1
    no_change: 0
         gain: [2x1 double]
      xoffset: [2x1 double]
  Name             Size            Bytes  Class     Attributes

  train_data      89x13             9256  double              

  Name            Size            Bytes  Class     Attributes

  train_pca      89x10             7120  double              

bestacc =
   98.8764
bestc =
     2
bestg =
    2.8284
bestacc =
   98.8764
bestc =
    5.1197
bestg =
    4.3773
bestacc =
   98.8764
bestc =
    2.7023
bestg =
    3.6726
Mean squared error = 2.71781 (regression)
Squared correlation coefficient = -1.#IND (regression)
bestCVaccuracy =
   97.7528
bestc =
    1.7411
bestg =
    5.2780
Accuracy = 100% (89/89) (classification)
Accuracy = 97.7528% (87/89) (classification)
accuracy =
  100.0000   97.7528
bestCVmse =
    0.0226
bestc =
    4.0039
bestg =
   11.8435
bestp =
    0.0923
Mean squared error = 0.00654143 (regression)
Squared correlation coefficient = 0.945718 (regression)
Mean squared error = 0.00193148 (regression)
Squared correlation coefficient = 0.0702999 (regression)
mse =
    0.0065    0.0019
r =
    0.9457    0.0703
Accuracy = 96.6292% (86/89) (classification)
score =
   96.6292
str =
Accuracy = 96.6292% (86/89) [Accuracy = #true / #total]
score =
   96.7742
str =
Precision = 96.7742% (30/31) [Precision = true_positive / (true_positive + false_positive)]
score =
   100
str =
Recall = 100% (30/30) [Recall = true_positive / (true_positive + false_negative)]
score =
   98.3607
str =
F-score = 98.3607% [F-score = 2 * Precision * Recall / (Precision + Recall)]
score =
    50
str =
BAC = 50% [BAC (Ballanced ACcuracy) = (Sensitivity + Specificity) / 2]
Accuracy = 86.6667% (234/270) (classification)
===some info of the data set===
#class is 2
类别标签为 1 -1 
支持向量数目 132,所占训练集样本数目比例 48.8889% （132/270）
===各种分类准确率===
整体分类准确率 = 86.6667% (234/270)
第 1 类分类准确率 = 80.8333% (97/120)
第 -1 类分类准确率 = 91.3333% (137/150)
CR = 
      accuracy: [0.8667 0.8083 0.9133]
    SVlocation: [132x1 double]
             b: -0.4245
             w: [132x1 double]
         alpha: [132x1 double]
Accuracy = 95.5056% (85/89) (classification)
时间已过 29.267572 秒。

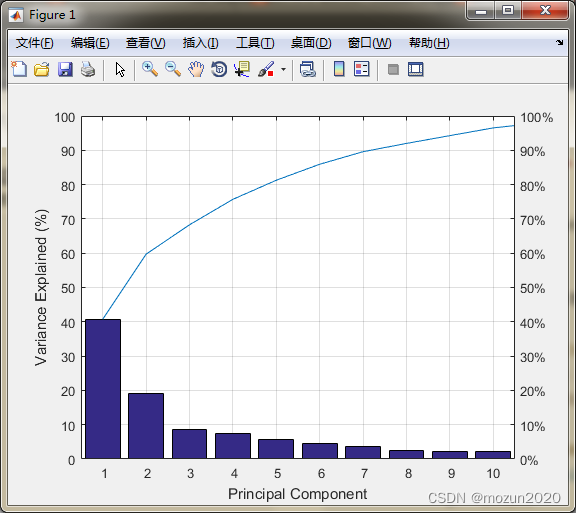
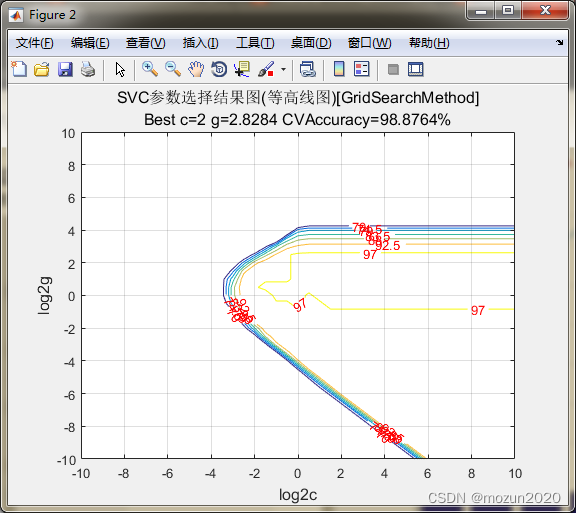
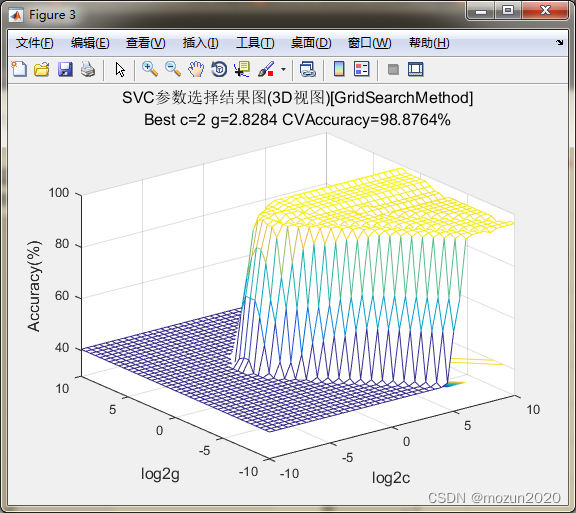
在这里插入图片描述

3. 小结

libsvm工具箱的应用还是很多的，前几章的仿真就是也需要这个工具箱中SVM相关的函数需要调用才一直没跑通，后面将工具箱中的路径包含到育英路径中去才完成仿真，工具箱里面的应用还是相对较多的，作为仿真来说也比较适合。对本章内容感兴趣或者想充分学习了解的，建议去研习书中第二十章节的内容。后期会对其中一些知识点在自己理解的基础上进行补充，欢迎大家一起学习交流。