4.5.1 梯度下降原理
求解这个凸函数的最低点通常采用“梯度?降法”。构造损失函数,把求
解最优参数θ的问题变成求解损失函数最小值的问题,便可以用梯度?降法求
解。
梯度?降法是调整参数θ使得损失函数J(θ)取得最小值的最基本方法之
一。从图像上看,就是在碗状结构的凸函数上取一个初始值,然后沿着楼梯一
步步挪动这个值,直到?降到最低点。
梯度?降法的求解过程就像是一个旅客?山的场景。如图 4-16 所示,假
设一位旅客在山上迷路了,身上没有水也没有食物,只有山?才有水源,因此
他需要找到最快的?山路径。此时山上的浓雾很大导致可视度很低,?山的路
径无法确定,他必须利用自己周围的信息找到?山的路径。在这种情况?,他
可以尝试以他当前的所处位置为基准,寻找这个位置最陡峭的方向,然后朝着
山的高度?降最多的地方走。
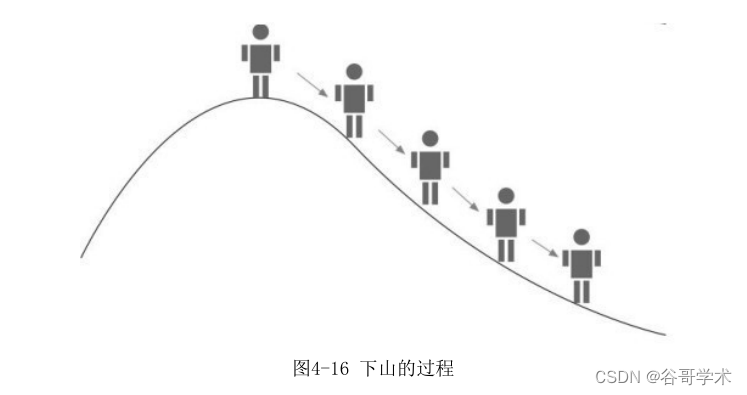
假设这座山最陡峭的地方没有办法通过肉眼立马观察出来,这位旅客需要
用身上的测量工具去确定哪个方向最陡峭。因此,他每走一段距离,需要耗费
一段时间来测量最陡峭的方向。为了在太阳?山之前到达山?,他需要尽可能
地减少测量方向的次数。这是一个博弈的过程,如果测量得频繁,虽然确保了
?山的方向最正确,但测量的耗时较长;如果测量得太少,又有偏离方向的风
险。所以需要找到一个合适的测量频率,确保?山的方向不错误,同时又不至
于耗费太多测量时间。
这个例子形象地说明了梯度?降法的求解过程。碗状凸函数就像两座山之
间的山脚一样,我们的目标是找到这个函数的最小值,也就是走到山?。根据
前面的场景假设,最快的?山方式就是找到当前位置最陡峭的方向,然后沿着
此方向向?走,对应到函数中就是找到最陡峭的下降梯度,然后朝着梯度相
反的方向走,才能让函数值下降得最快 ,如图4-17所示。
在函数很接近最低点的时候,如果走得太快,很容易错过最低点。因此需
要设置一个参数,控制每一次走的距离,这个参数叫作学习率。学习率不宜太
大也不宜太小,太小的话可能导致迟迟走不到最低点,太大的话会容易错过最
低点,如图4-18所示。在实际项目中,一开始我们可以采用稍大的学习率,当
接近最低点的时候,适当降低学习率,这样能确保用最短的时间找到准确的函
数最低点。
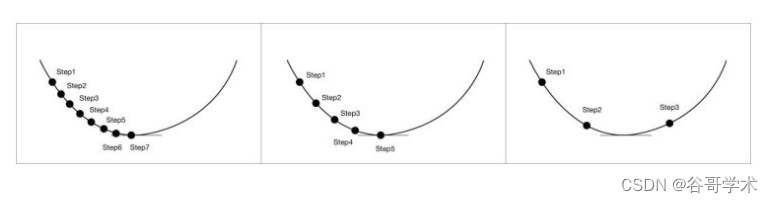
图4-18 学习率太大或太小都不合适
4.5.2 梯度下降的特点
梯度?降法的求解过程是,以当前位置负梯度方向作为搜索方向快速?降
求出最小值。因为负梯度方向为当前位置的最快?降方向,所以梯度?降法也
被称为“最速?降法”。在梯度?降的过程中,越接近目标值,步长越小,前
进越慢。一般按以?的步骤进行:
(1)给定θ的值。
(2)求当前θ位置处的梯度。
(3)改变θ的值,让损失函数J(θ)按梯度?降的方向减小。
(4)求得局部极小值。
由此我们可以通过梯度?降法计算逻辑回归中损失函数的最小值,计算过
程在此不再展开?述。对于产品经理来说,只需要掌握这个方法的核心思想即
可。值得注意的是,梯度?降法并非一定能找到全局最小值,很多时候同样只
能找到一个局部最小值。这就好比旅客在使用梯度?降法的过程中遇到了两座
山之间的山谷,虽然在山谷附近这是一个最低点,但从整座山来看山脚才是最
低点。为了解决这个问题,我们只能多次运行,随机化初始?山点,希望通过
多次?山的方式寻找到整座山的最低点。
也因为这个原因,目前常用的梯度?降法有两种不同的进行方式。第一种
方法是批量梯度?降法。这种方法需要遍历全部的样本集之后统一计算全局损
失函数,使得最终求解的是全局的最优解。在采用批量梯度?降法的时候,每
次更新参数时所有样本都需要遍历一次,计算量大,因此它不适用于样本规模
比较大的情况。
另一种方法是随机梯度?降法,这种方法的特点是每遍历一个样本就计算
一次损失函数,虽然不是每次迭代得到的损失函数都向着全局最优的方向前
进,但是整体方向是向全局最优解前进的,最终得出的结果往往会在最优解的
附近震荡,所以我们找到的只是近似最优解。当训练样本过大时,我们可以选
择这种退而求其次的方法,虽然只是近似的最优解,但是在很多场景?已经能
够满足我们的使用需求了。
为了克服这两种方法的缺点,在实际项目中我们通常采用一种比较折中的
方法,即采用小批量的梯度?降法。这种方法将数据分为若干批次,按批更新
参数,这样,一批的数据共同决定本次梯度?降的方向,?降的过程中不容易
跑偏,减少了随机性,同时计算量也相对比较小,是一种比较实际的方法。
4.6 产品经理的经验之谈
本章进入到正式的算法讲解,首先学习的是回归分析模型。回归分析是最
基础、最常用的算法之一,它是一种确定两个及两个以上变量间相互依赖关系
的统计分析方法。当自变量与因变量确实存在某种关系时,建立回归方程能够
挖掘其中的规律。因此,作为自变量的因素与作为因变量的预测对象是否有
关,相关程度如何,成为进行回归分析首要解决的问题。
回归分析按照涉及的变量数量,可分为一元回归分析与多元回归分析;按
照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
本章主要学习一元线性回归、多元线性回归及逻辑回归的算法原理与实现方
法。
在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条
直线近似表示,这种情况称为一元线性回归。如果包括两个或两个以上的自变
量,且因变量和自变量之间是线性关系,则称为多元线性回归。无论是一元线
性回归还是多元线性回归,我们都很难找到完全拟合所有真实样本点的函数,
预测点和样本点之间总是存在误差。因此寻找最理想的拟合函数的过程变成了
寻找使得误差最小的函数的过程,在数学上表示为损失函数的最小化求解。通
常我们可以使用最小二乘估计法求解损失函数的最小值。
如何定?损失值最小是评判模型拟合程度的关键,预测值与样本值之间的
误差并非完全是由于目标因变量引起的,还有其他的影响因素。因此设定评价
指标的目的是为了找到模型变量带来的影响以及非模型变量带来的影响。在统
计学中常用判定系数R 2 判断回归方程的拟合程度,R 2 越大,代表回归线拟合
程度越好;R 2 越小,代表回归线拟合程度越差。
逻辑回归是在线性回归的基础上,套用了一个激活函数,即sigmoid函
数,使得原本敏感的函数变得更柔和。正因为这个激活函数,我们才能将原本
对正类或负类的结果预测,转化为对正类或负类的概率预测。
逻辑回归本质上仍然是一个线性回归模型,只是在特征到结果的映射中加
入了一层函数映射,先把特征线性求和,然后使用函数g(z)作为假设函数求
解。我们看到的参数z实际上也是一个线性回归的方程,只不过在这里用符号
表示。因此逻辑回归的求解方法与线性回归相同,都是通过构造损失函数的方
法?近最优解。在逻辑回归中,通常使用梯度?降法求解损失函数的最小值。?
?