[人工智能]2018/GAN:Self-Attention Generative Adversarial Networks自我注意生成对抗网络

论文下载
代码开源

0.摘要

在本文中，我们提出了自我注意生成对抗网络(Self-Attention Generative Adversarial Network, SAGAN)，该网络允许对图像生成任务进行注意力驱动的长期依赖建模。传统的卷积GANs在低分辨率特征图中仅以空间局部点为函数来生成高分辨率的细节。在SAGAN中，可以使用所有特征位置的线索来生成细节。此外，该鉴别器还可以检查图像远处部分的高细节特征是否一致。此外，最近的研究表明，生成器的条件影响GAN性能。利用这一见解，我们将光谱归一化应用于GAN生成器，并发现这改善了训练动力学。提出的SAGAN比之前的工作表现更好1，将最佳Inception score(IS)从36.8提高到52.52，并将具有挑战性的ImageNet数据集上的起始距离从27.62降低到18.65。注意层的可视化显示，生成器利用了与物体形状相对应的邻域，而不是固定形状的局部区域。

1.概述

图1所示。提出的SAGAN通过利用图像远处部分的互补特征而不是固定形状的局部区域来生成一致的目标/场景来生成图像。在每一行中，第一张图像显示了五个具有代表性的查询位置，并使用颜色编码点。其他五幅图是这些查询位置的注意力地图，用相应的颜色编码的箭头总结了最受关注的区域。

图像合成是计算机视觉中的一个重要问题。随着生成对抗网络(GANs)的出现，这一方向取得了显著的进展(Goodfellow等人，2014)，尽管仍存在许多开放问题(Odena, 2019)。基于深度卷积网络的GANs (Radford et al.， 2016;Karras等人，2018;Zhang等人)尤其成功。然而，通过仔细检查这些模型生成的样本，我们可以观察到卷积GANs (Odena等人，2017;Miyato等人，2018;Miyato & Koyama, 2018)在多类数据集上训练时(例如，ImageNet (Russakovsky等人，2015))，在建模某些图像类时比其他图像类要困难得多。例如，虽然最先进的ImageNet GAN模型(Miyato & Koyama, 2018)擅长在很少的结构约束下合成图像类(例如，海洋、天空和景观类，它们更多地通过纹理而不是几何来区分)，但它不能捕捉在某些类中一致出现的几何或结构模式(例如，狗通常用逼真的皮毛纹理绘制，但没有明确定义的单独的脚)。一个可能的解释是，之前的模型严重依赖于卷积来建模不同图像区域之间的依赖性。由于卷积算子具有局部的接收域，因此只有经过几层卷积之后才能处理长距离依赖关系。由于各种原因，这可能会阻止了解长期依赖关系:一个小模型可能无法表示它们，优化算法可能难以发现仔细协调多层以捕获这些依赖关系的参数值，而且这些参数化在统计上可能很脆弱，当应用到以前不可见的输入时容易失败。增大卷积核的大小可以增加网络的表示容量，但同时也会失去利用局部卷积结构获得的计算和统计效率。自我注意(Cheng等人，2016;Parikh等人，2016;另一方面，V aswani等人，2017)在模拟远程依赖关系的能力与计算和统计效率之间表现出更好的平衡。自我注意模块将某一位置的响应计算为所有位置特征的加权和，其中权重(或注意向量)的计算只需要很小的计算成本。
在本研究中，我们提出了自我注意生成对抗网络(SAGANs)，该网络将自我注意机制引入到卷积生成对抗网络中。自我注意模块是卷积的补充，并有助于建模的长期，多层次依赖的图像区域。有了自我关注的能力，生成器可以绘制出图像，其中每个位置的细节都与图像远处部分的细节进行了仔细的协调。此外，该鉴别器还能更准确地对全局图像结构施加复杂的几何约束
除了自我注意之外，我们还结合了最近关于网络条件反射与GAN性能的见解。Odena等人的工作(2018年)表明，条件良好的生成器往往表现得更好。我们建议使用光谱归一化技术对GAN发生器进行良好的调节，该技术此前只应用于鉴别器(Miyato等人，2018)。
我们在ImageNet数据集上进行了大量的实验，以验证所提出的自我注意机制和稳定技术的有效性。SAGAN通过将IS的最佳得分从36.8提高到52.52，并将Fréche IS距离从27.62降低到18.65，在图像合成方面显著优于之前的工作。注意层的可视化显示，生成器利用了与物体形状相对应的邻域，而不是固定形状的局部区域。

2.相关工作

2.1.GAN

GANs在各种图像生成任务中取得了巨大的成功，包括图像到图像的转换(Isola et al.， 2017;Zhu等人，2017;泰格曼等人，2017;Liu和Tuzel, 2016;薛等，2018;Park等人，2019)，图像超分辨率(Ledig等人，2017;Snderby等人，2017)和文本到图像合成(Reed等人，2016b;a;Zhang等人，2017;Hong et al.， 2018)。尽管这一成功，众所周知，GANs的训练是不稳定的，对超参数的选择很敏感。有几项工作试图通过设计新的网络架构来稳定GAN训练动力学并提高样本多样性(Radford et al.， 2016;Zhang等人，2017;Karras等人，2018;2019)，修改学习目标和动态(Arjovsky等人，2017;Salimans等人，2018;梅茨等人，2017;Che等人，2017;赵等人，2017;Jolicoeur-Martineau, 2019)，添加正则化方法(Gulrajani等人，2017;Miyato et al.， 2018)和引入启发式技巧(Salimans et al.， 2016;Odena等人，2017;Azadi等人，2018)。最近，Miyato等人(Miyato et al.， 2018)提出限制鉴别器中权重矩阵的谱范数，以约束鉴别器函数的Lipschitz常数。结合基于投影的鉴别器(Miyato & Koyama, 2018)，光谱归一化模型大大改善了ImageNet上的类条件图像生成。

2.2.注意力模型

最近，注意力机制已经成为必须捕获全局依赖关系的模型的组成部分(Bahdanau等人，2014;Xu等人，2015;杨等，2016;Gregor等人，2015;Chen等人，2018)。特别是自我注意(Cheng等人，2016;Parikh et al.， 2016)，也被称为intra-attention，通过关注同一序列中的所有位置来计算序列中某个位置的响应。V aswani等人(V aswani et al.， 2017)证明，机器翻译模型仅通过使用自我注意模型就可以获得最先进的结果。Parmar等人(Parmar et al.， 2018)提出了一种Image Transformer模型，将自我注意添加到自回归模型中，用于生成图像。Wang等人(Wang et al.， 2018)将自我注意形式化为一种非局部操作，以建模视频序列中的时空相关性。尽管取得了这些进展，但在GANs中还没有对自我注意进行探讨。(AttnGAN (Xu et al.， 2018)对输入序列中的单词嵌入使用注意，但对内部模型状态不使用自我注意)。SAGAN学习在图像的内部表征中有效地找到全局的、长期的依赖关系。

3.自注意生成对抗网络Self-Attention Generative Adversarial Networks

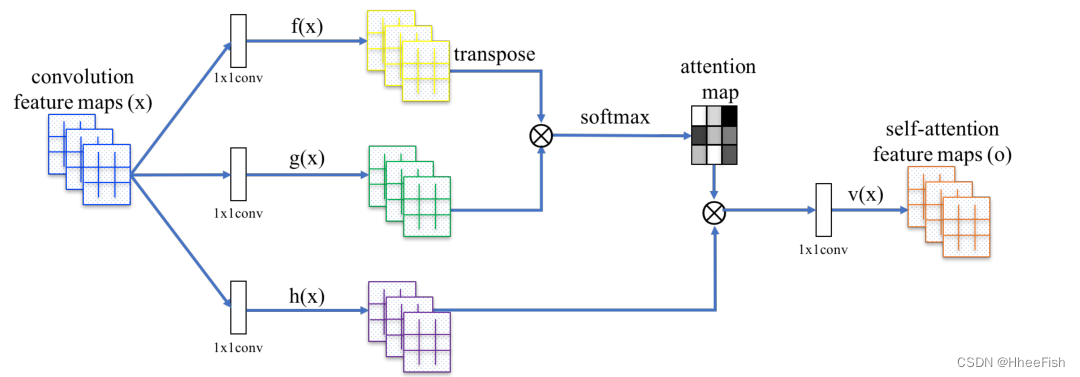
图2。SAGAN的自我注意模块。?表示矩阵乘法。对每一行执行softmax操作

大多数基于GAN的模型(Radford等人，2016;Salimans等人，2016;Karras等人，2018)的图像生成使用卷积层构建。卷积处理的信息在一个局部邻域，因此使用卷积层单独是计算效率低的建模远程依赖图像。在本节中，我们采用了(Wang et al.， 2018)的非局部模型，将自我注意引入GAN框架，使生成器和鉴别器都能够有效地建模广泛分离的空间区域之间的关系。由于其自我注意模块(参见图2)，我们将所提出的方法称为自我注意生成对抗网络(Self-Attention Generative Adversarial Networks, SAGAN)。
首先将之前隐藏层的图像特征x∈R^C×N转化为两个特征空间f, g来计算注意力，其中f(x) = W_f^x, g(x) = W_g^x,

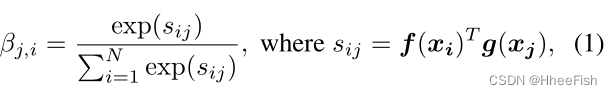
β_j,i表示模型在合成第j个区域时对第i个位置的关注程度。其中C为通道数，N为前一隐含层特征的特征位置数。注意层的输出是o = (o₁, o₂，…、o_j……o_N)∈R^C×N，其中，

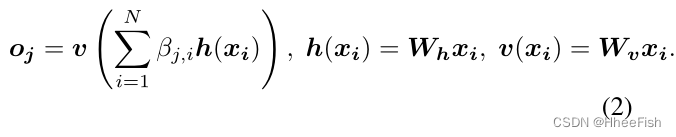
在上述公式中，W_g∈R^Cˉ×C、W_f∈R^Cˉ×C、W_h∈R^Cˉ×C和W_v∈R^C×C是学习到的权重矩阵，它们被实现为1×1卷积。因为当我们将Cˉ的通道数减少为C/k(在ImageNet上经过几个训练期后，k = 1,2,4,8)时，我们没有注意到任何显著的性能下降。为了提高内存效率，我们在所有实验中都选择k = 8(即Cˉ = C/8)。
此外，我们进一步将注意力层的输出乘以一个比例参数，并添加回输入特征图。因此，最终输出为，

其中γ是一个可学习的标量，初始化为0。引入可学习的γ使得网络首先依赖于局部区域的线索——因为这更容易——然后逐渐学会赋予非局部证据更多的权重。我们这么做的原因很简单:我们想先学习简单的任务，然后逐步增加任务的复杂性。在SAGAN中，提出的注意模块已应用于生成器和鉴别器，它们通过最小化对抗性损失的铰链版本以交替方式进行训练(Lim & Ye, 2017;Tran等人，2017;Miyato et al.， 2018)，

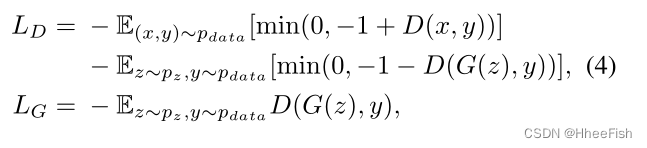
4.稳定GANs训练的技巧

我们还研究了两种技术来稳定GANs在具有挑战性的数据集上的训练。首先，我们在生成器和鉴别器中使用光谱归一化(Miyato et al.， 2018)。其次，我们确认了双时间尺度更新规则(TTUR) (Heusel et al.， 2017)是有效的，我们主张特别使用它来解决正则化鉴别器中的慢学习问题。

4.1. 生成器和鉴别器的光谱归一化

Miyato等人(Miyato et al.， 2018)最初提出通过对鉴别器网络应用光谱归一化来稳定GANs的训练。这样做通过限制每一层的谱范数来限制鉴别器的李普希茨常数。与其他归一化技术相比，谱归一化不需要额外的超参数调整(将所有权值层的谱范数设置为1在实际应用中始终表现良好)。此外，计算成本也相对较小。
我们认为，基于最近的证据，发电机的条件调节是GANs性能的重要因果因素，发电机也可以受益于光谱归一化(Odena等人，2018)。频谱归一化可以防止参数幅度的增大，避免异常梯度。我们通过实验发现，对产生器和鉴别器进行光谱归一化可以使每次生成器更新使用更少的鉴别器更新，从而显著降低训练的计算成本。该方法还显示出更稳定的训练行为。

4.2. 生成器和鉴别器更新的不平衡学习率

在之前的工作中，鉴别器的正则化(Miyato et al.， 2018;Gulrajani等人，2017)经常减慢GANs的学习过程。在实践中，使用正则化鉴别器的方法通常在训练过程中，每个生成器更新步骤需要多个(例如，5)鉴别器更新步骤。独立地，Heusel等人(Heusel et al.， 2017)主张对生成器和鉴别器使用单独的学习率(TTUR)。我们建议使用TTUR来补偿正则化鉴别器学习缓慢的问题，使每个生成器步骤使用更少的鉴别器步骤成为可能。使用这种方法，我们能够在相同的时间内产生更好的结果。

5.实验

图4。128×128示例随机生成的基线模型和我们的模型“SN on G/D”和“SN on G/D+TTUR”

为了评估所提出的方法，我们在LSVRC2012 (ImageNet)数据集上进行了大量实验(Russakovsky et al.， 2015)。首先，在5.1节中，我们提出了旨在评估稳定GANs训练的两种技术的有效性的实验。接下来，在第5.2节中研究了所提出的自我注意机制。最后，我们的SAGAN方法与最先进的方法进行了比较(Odena等人，2017;Miyato & Koyama, 2018)在5.3节中的图像生成任务。模型在每个4个gpu上使用同步SGD(众所周知，异步SGD存在困难，参见例(Odena, 2016))训练约2周。
评价指标
我们选择Inception评分(IS) (Salimans et al.， 2016)和Fr′echet Inception距离(FID) (Heusel et al.， 2017)进行定量评估。尽管存在替代方案(Zhou等人，2019;Khrulkov和Oseledets, 2018;Olsson et al.， 2018)，它们并没有被广泛使用。Inception评分(Salimans et al.， 2016)计算条件类分布和边缘类分布之间的KL散度。Inception分数越高，图像质量越好。我们包含Inception得分，因为它被广泛使用，因此可以将我们的结果与以前的工作进行比较。然而，重要的是要理解Inception分数有严重的限制—它主要是为了确保模型生成的样本可以被确信地识别为属于一个特定的类，并且模型从许多类中生成样本，不一定要评估细节的真实性或类内多样性。FID是一种更有原则、更全面的衡量标准，在评估生成样本的真实性和变异性时，已被证明与人类评估更一致(Heusel et al.， 2017)。FID计算在Inception-v3网络的特征空间中生成的图像与真实图像之间的Wasserstein-2距离
除了对整个数据分布(即。， ImageNet中的所有1000类图像)，我们还计算每个类中生成的图像和数据集图像之间的FID(称为intra FID (Miyato & Koyama, 2018))。较低的FID和内部FID值意味着合成数据分布与真实数据分布之间的距离更近。在我们所有的实验中，每个模型随机生成50k个样本，计算Inception分数、FID和intra FID。
网络结构和实现细节。我们训练的所有SAGAN模型都旨在生成128×128图像。默认情况下，生成器和鉴别器中的层都使用了光谱归一化(Miyato et al.， 2018)。类似于(Miyato & Koyama, 2018)， SAGAN在生成器中使用条件批归一化，在鉴别器中使用投影。对于所有模型，我们使用β₁ = 0和β₂ = 0.9的Adam优化器(Kingma & Ba, 2015)进行训练。缺省情况下，鉴别器的学习率为0.0004，生成器的学习率为0.0001。

5.1. 评估提出的稳定技巧

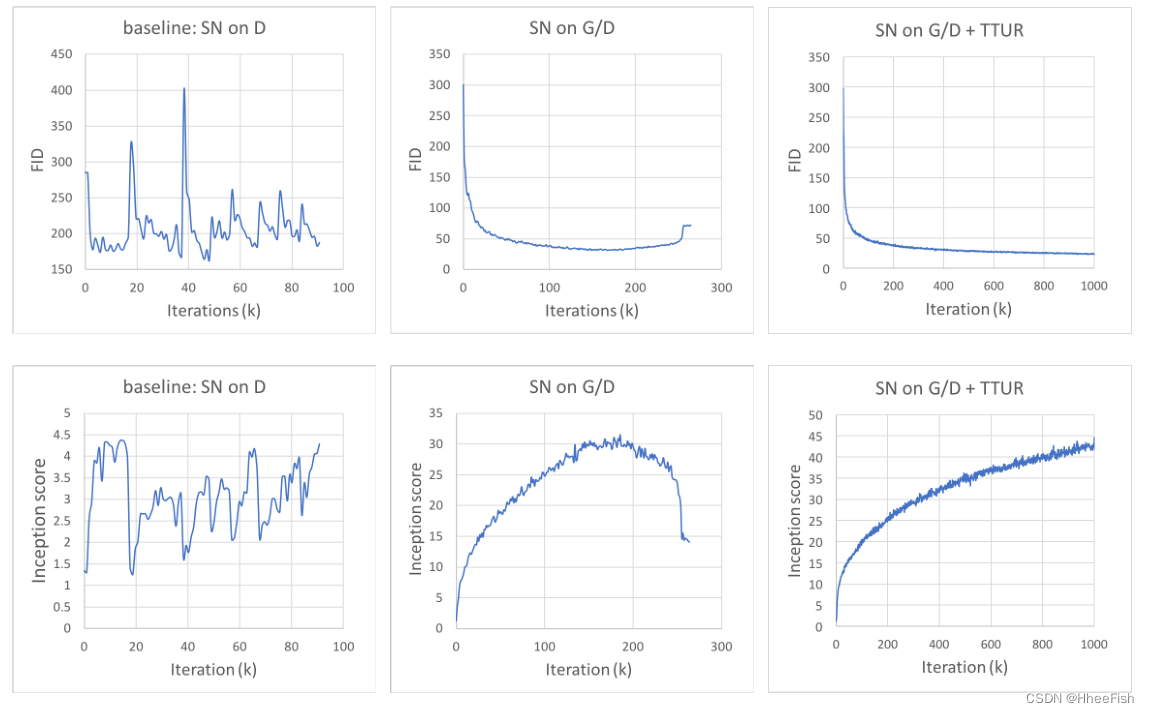
图3。训练曲线的基线模型和我们的模型与提出的稳定技术，“SN上的G/D”和两时间尺度学习率(TTUR)。对所有模型G和D进行1:1均衡更新训练

在本节中，我们进行了实验来评估提出的稳定技术的有效性，即，将光谱归一化(SN)应用到生成器和利用不平衡学习率(TTUR)。在图3中，我们的模型“SN on G/D”和“SN on G/D+TTUR”与基于最先进的图像生成方法实现的基线模型进行了比较(Miyato et al.， 2018)。在该基线模型中，仅在鉴别器中使用SN。当我们对判别器(D)和生成器(G)进行1:1均衡更新的训练时，训练变得非常不稳定，如图3最左边的子图所示。它在训练早期表现出模式崩溃。例如，图4左上角的子图展示了基线模型在第10k次迭代时随机生成的一些图像。虽然在原论文(Miyato et al.， 2018)中，对D和G采用5:1的不平衡更新大大缓解了这种不稳定的训练行为，但为了提高模型的收敛速度，采用1:1的平衡更新进行稳定训练的能力是可取的。因此，使用我们提出的技术意味着在相同的挂钟时间下，该模型可以产生更好的结果。因此，不需要为生成器和鉴别器寻找合适的更新比。如图3中间子图所示，在发生器和鉴别器中同时添加SN，即使是1:1均衡更新训练，我们的模型“SN on G/D”也会得到很大的稳定。但在训练过程中，样本的质量并不是单调提高的。例如，通过FID和IS测量的图像质量在第260k次迭代时开始下降。在图4中可以找到该模型在不同迭代过程中随机生成的示例图像。当我们同样使用不平衡学习率训练判别器和生成器时，我们的模型“SN on G/D+TTUR”在整个训练过程中图像质量单调提高。如图3和图4所示，在一百万次训练迭代中，我们没有观察到样本质量或FID或Inception分数的任何显著下降。因此，定量结果和定性结果都证明了所提出的稳定技术对GANs训练的有效性。它们还表明，两种技术的效果至少在一定程度上是叠加的。在其余的实验中，所有的模型都对生成器和鉴别器进行了光谱归一化处理，并使用不平衡学习率对生成器和鉴别器进行1:1更新的训练。

5.2. Self-Attention机制

表1。GANs中自我注意与剩余块的比较。这些块被添加到网络的不同层中。所有的模型都经过了一百万次迭代的训练，并且报告了最好的Inception分数(IS)和Fr′echet Inception距离(FID)。F eatk意味着在k×k功能图中添加自我关注

图5。注意力地图的可视化。这些图像是由萨根生成的。我们将使用注意力的最后一个生成器层的注意力地图可视化，因为这一层最接近输出像素，并且最容易投射到像素空间并解释。在每个单元格中，第一张图像显示了三个具有代表性的查询位置，这些位置用颜色编码的点表示。其他三幅图像是这些查询位置的注意力地图，用相应的颜色编码的箭头总结了最受关注的区域。我们观察到这个网络学会了根据颜色和纹理的相似性来分配注意力，而不仅仅是空间邻接(见左上角的单元格)。我们还发现，尽管一些查询点在空间位置上非常接近，但它们的注意力地图可能非常不同，如左下角单元格所示。如图右上单元格所示，SAGAN能够画出两条腿泾渭分明的狗。蓝色的查询点表示注意有助于获得正确的关节区域结构。更多关于习得注意图属性的讨论请参阅本文。

为了探究所提出的自我注意机制的效果，我们通过在产生器和鉴别器的不同阶段添加自我注意机制来构建多个SAGAN模型。如表1所示，在中高级特征图(如f eat32和f eat64)中具有自我注意机制的SAGAN模型比在低级特征图(如f eat8和f eat16)中具有自我注意机制的模型取得了更好的性能。例如，“SAGAN, f eat8”模型的FID由22.98提高到18.28，“SAGAN, f eat32”。原因在于，自我注意接收到更多的证据，并且有更多的自由选择具有较大特征映射的条件(即，对于较大的特征映射，它是卷积的补充)，但在对较小的特征映射(如8×8)建模依赖关系时，它起着类似于局部卷积的作用。结果表明，注意机制使产生器和鉴别器都具有更强的能力来直接建模特征图中的远程依赖关系。此外，我们的SAGAN模型与无注意基线模型(表1的第二列)的比较进一步表明了所提出的自我注意机制的有效性。
与相同参数数的残差块相比，自注意块也取得了更好的效果。例如，当我们用8×8 feature maps中的残差块替换self-attention block时，训练是不稳定的，这导致了性能的显著下降(例如，FID从22.98增加到42.13)。即使在训练顺利的情况下，用残差块替换自我注意块仍然会导致FID和Inception分数更差的结果。(例如，特征图32 × 32中的FID 18.28 vs 27.33)。这一比较表明，使用SAGAN带来的性能改进不仅仅是因为模型深度和容量的增加。
为了更好地理解在生成过程中学习了什么，我们在SAGAN中可视化了生成器对不同图像的注意权重。图5和图1显示了一些值得注意的示例图像。关于学习注意图的一些属性的描述，请参见图5的说明。

5.3. 与最先进的比较

表2。提出的SAGAN与最先进的GAN模型的比较(Odena等人，2017;Miyato & Koyama, 2018)用于ImageNet上的类条件图像生成。根据官方公布的权重计算出sngan的FID。

图6。由SAGAN为不同的类生成的128x128示例图像。每行显示一个类的示例。在最左边的一栏，列出了我们的SAGAN内部FID(左)和最先进的方法(Miyato & Koyama, 2018))(右)。

我们还将我们的SAGAN与最先进的GAN模型进行了比较(Odena等人，2017;Miyato & Koyama, 2018)用于ImageNet上的类条件图像生成。如表2所示，我们提出的SAGAN实现了最好的Inception分数，内部FID和FID。拟议的SAGAN显著提高了最佳published Inception score，从36.8提高到52.52。SAGAN实现的较低FID(18.65)和intra FID(83.7)也表明，SAGAN通过使用自我注意模块对图像区域之间的远程依赖性建模，可以更好地逼近原始图像分布。
图6显示了一些ImageNet代表性类的比较结果和生成的图像。我们观察到，在合成具有复杂几何或结构模式的图像类(如金鱼和圣伯纳犬)方面，我们的SAGAN比最先进的GAN模型(Miyato & Koyama, 2018)取得了更好的性能(即，较低的内部FID)。对于结构约束较少的类(例如，山谷、石墙和珊瑚真菌，它们更多地通过纹理而不是几何来区分)，我们的SAGAN显示出比基线模型更少的优势(Miyato & Koyama, 2018)。同样，原因是SAGAN中的自我注意是对卷积的补充，用于捕获在几何或结构模式中一致发生的长期、全局级别的依赖关系，但在为简单纹理建模依赖关系时，其作用与局部卷积类似。

6. 结论

在本文中，我们提出了自注意生成对抗网络(SAGANs)，该网络将自我注意机制融入到GAN框架中。自我注意模块在建模远程依赖方面是有效的。此外，我们表明，光谱归一化应用于发生器稳定GAN训练和TTUR加快训练正则化鉴别器。SAGAN在ImageNet上的类条件图像生成方面实现了最先进的性能。

参考文献

Arjovsky, M., Chintala, S., and Bottou, L. Wasserstein GAN. arXiv:1701.07875, 2017.
Azadi, S., Olsson, C., Darrell, T., Goodfellow, I., and Odena, A. Discriminator rejection sampling. arXiv preprint arXiv:1810.06758, 2018.
Bahdanau, D., Cho, K., and Bengio, Y . Neural machine translation by jointly learning to align and translate. arXiv:1409.0473, 2014.
Brock, A., Donahue, J., and Simonyan, K. Large scale gan training for high fidelity natural image synthesis. arXiv preprint arXiv:1809.11096, 2018.
Che, T., Li, Y ., Jacob, A. P ., Bengio, Y ., and Li, W. Mode regularized generative adversarial networks. In ICLR, 2017.
Chen, X., Mishra, N., Rohaninejad, M., and Abbeel, P . Pixelsnail: An improved autoregressive generative model. In ICML, 2018.
Cheng, J., Dong, L., and Lapata, M. Long short-term memory-networks for machine reading. In EMNLP, 2016.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A. C., and Bengio, Y . Generative adversarial nets. In NIPS, 2014.
Gregor, K., Danihelka, I., Graves, A., Rezende, D. J., and Wierstra, D. DRAW: A recurrent neural network for image generation. In ICML, 2015.
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V ., and Courville, A. C. Improved training of wasserstein GANs. In NIPS, 2017.
Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., and Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In NIPS, pp. 6629–6640, 2017.
Hong, S., Y ang, D., Choi, J., and Lee, H. Inferring semantic layout for hierarchical text-to-image synthesis. In CVPR, 2018.
Isola, P ., Zhu, J.-Y ., Zhou, T., and Efros, A. A. Image-toimage translation with conditional adversarial networks. In CVPR, 2017.
Jolicoeur-Martineau, A. The relativistic discriminator: a key element missing from standard GAN. In ICLR, 2019. Karras, T., Aila, T., Laine, S., and Lehtinen, J. Progressive growing of GANs for improved quality, stability, and variation. In ICLR, 2018.
Karras, T., Laine, S., and Aila, T. A style-based generator architecture for generative adversarial networks. In CVPR, 2019. Khrulkov, V . and Oseledets, I. Geometry score: A method for comparing generative adversarial networks. arXiv preprint arXiv:1802.02664, 2018.
Kingma, D. P . and Ba, J. Adam: A method for stochastic optimization. In ICLR, 2015.
Ledig, C., Theis, L., Huszar, F., Caballero, J., Aitken, A., Tejani, A., Totz, J., Wang, Z., and Shi, W. Photo-realistic single image super-resolution using a generative adversarial network. In CVPR, 2017.
Lim, J. H. and Y e, J. C. Geometric GAN. arXiv:1705.02894, 2017.
Liu, M. and Tuzel, O. Coupled generative adversarial networks. In NIPS, 2016.
Metz, L., Poole, B., Pfau, D., and Sohl-Dickstein, J. Unrolled generative adversarial networks. In ICLR, 2017.
Miyato, T. and Koyama, M. cGANs with projection discriminator. In ICLR, 2018.
Miyato, T., Kataoka, T., Koyama, M., and Y oshida, Y . Spectral normalization for generative adversarial networks. In ICLR, 2018.
Odena, A. Faster asynchronous sgd. arXiv preprint arXiv:1601.04033, 2016.
Odena, A. Open questions about generative adversarial networks. Distill, 2019. doi: 10.23915/distill.00018. https://distill.pub/2019/gan-open-problems. Odena, A., Olah, C., and Shlens, J. Conditional image synthesis with auxiliary classifier GANs. In ICML, 2017.
Odena, A., Buckman, J., Olsson, C., Brown, T. B., Olah, C., Raffel, C., and Goodfellow, I. Is generator conditioning causally related to GAN performance? In ICML, 2018.
Olsson, C., Bhupatiraju, S., Brown, T., Odena, A., and Goodfellow, I. Skill rating for generative models. arXiv preprint arXiv:1808.04888, 2018.
Parikh, A. P ., T¨ackstr¨om, O., Das, D., and Uszkoreit, J. A decomposable attention model for natural language inference. In EMNLP, 2016.
Park, T., Liu, M., Wang, T., and Zhu, J. Semantic image synthesis with spatially-adaptive normalization. In CVPR, 2019. Parmar, N., V aswani, A., Uszkoreit, J., ukasz Kaiser, Shazeer, N., and Ku, A. Image transformer. arXiv:1802.05751, 2018.
Radford, A., Metz, L., and Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. In ICLR, 2016.
Reed, S., Akata, Z., Mohan, S., Tenka, S., Schiele, B., and Lee, H. Learning what and where to draw. In NIPS, 2016a.
Reed, S., Akata, Z., Yan, X., Logeswaran, L., Schiele, B., and Lee, H. Generative adversarial text-to-image synthesis. In ICML, 2016b. Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., Berg, A. C., and Fei-Fei, L. ImageNet large scale visual recognition challenge. IJCV, 2015.
Salimans, T., Goodfellow, I. J., Zaremba, W., Cheung, V ., Radford, A., and Chen, X. Improved techniques for training GANs. In NIPS, 2016.
Salimans, T., Zhang, H., Radford, A., and Metaxas, D. N. Improving GANs using optimal transport. In ICLR, 2018.
Snderby, C. K., Caballero, J., Theis, L., Shi, W., and Huszar, F. Amortised map inference for image super-resolution. In ICLR, 2017.
Taigman, Y ., Polyak, A., and Wolf, L. Unsupervised crossdomain image generation. In ICLR, 2017.
Tran, D., Ranganath, R., and Blei, D. M. Deep and hierarchical implicit models. arXiv:1702.08896, 2017.
V aswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., and Polosukhin, I. Attention is all you need. arXiv:1706.03762, 2017.
Wang, X., Girshick, R., Gupta, A., and He, K. Non-local neural networks. In CVPR, 2018.
Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A. C., Salakhutdinov, R., Zemel, R. S., and Bengio, Y . Show, attend and tell: Neural image caption generation with visual attention. In ICML, 2015.
Xu, T., Zhang, P ., Huang, Q., Zhang, H., Gan, Z., Huang, X., and He, X. AttnGAN: Fine-grained text to image generation with attentional generative adversarial networks. In CVPR, 2018.
Xue, Y ., Xu, T., Zhang, H., Long, L. R., and Huang, X. SegAN: Adversarial network with multi-scale L1 loss for medical image segmentation. Neuroinformatics, pp. 1–10, 2018.
Y ang, Z., He, X., Gao, J., Deng, L., and Smola, A. J. Stacked attention networks for image question answering. In CVPR, 2016.
Zhang, H., Xu, T., Li, H., Zhang, S., Wang, X., Huang, X., and Metaxas, D. N. StackGAN++: Realistic image synthesis with stacked generative adversarial networks. TPAMI. Zhang, H., Xu, T., Li, H., Zhang, S., Wang, X., Huang, X., and Metaxas, D. StackGAN: Text to photo-realistic image synthesis with stacked generative adversarial networks. In ICCV, 2017.
Zhao, J., Mathieu, M., and LeCun, Y . Energy-based generative adversarial network. In ICLR, 2017.
Zhou, S., Gordon, M., Krishna, R., Narcomey, A., Morina, D., and Bernstein, M. S. HYPE: human eye perceptual evaluation of generative models. CoRR, abs/1904.01121, 2019. URL http://arxiv.org/ abs/1904.01121. Zhu, J.-Y ., Park, T., Isola, P ., and Efros, A. A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In ICCV, 2017.