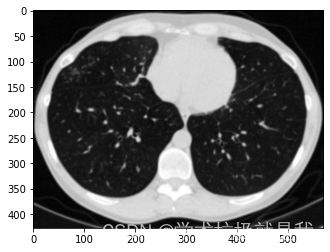
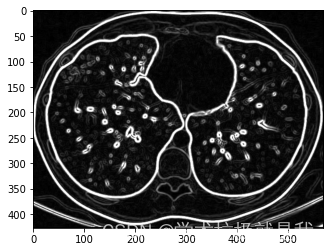
在理想情况下,对图像应用边缘检测器的结果可能会导致一组连接曲线,表明物体的边界,表面标记的边界以及对应于表面方向不连续点的曲线。
因此,对图像应用边缘检测算法可以显著减少要处理的数据量,因此可以过滤掉可能被认为不太相关的信息,同时保留图像的重要结构属性。
如果边缘检测步骤成功,则后续解释原始图像中的信息内容的任务可以大大简化。然而,从中等复杂程度的真实图像中获得这种理想边缘并不总是可能的。
从非平凡图像中提取的边缘往往会受到碎片化的阻碍,这意味着边缘曲线不连接,缺失的边缘片段以及与图像中有趣现象不对应的虚假边缘,从而使后续解释图像数据的任务复杂化。
边缘检测是图像处理、图像分析、图像模式识别和计算机视觉技术的基本步骤之一。
边缘检测的方法有很多,但大多数可以分为两类,基于搜索的和基于零交叉的。
基于搜索的方法首先计算边缘强度的度量,通常是一阶导数表达式,如梯度幅度,然后使用边缘的局部方向(通常是梯度方向)的计算估计来搜索梯度幅度的局部方向最大值。
基于零交叉的方法在从图像计算的二阶导数表达式中寻找零交叉,以找到边缘,通常是拉普拉斯算子的零交叉或非线性微分表达式的零交叉。
已经发表的边缘检测方法主要不同于应用的平滑滤波器类型和边缘强度的计算方法。由于许多边缘检测方法依赖于图像梯度的计算,它们在x和y方向上用于计算梯度估计的滤波器类型也不同。
?在一阶方法中,不同的梯度算子可以应用于估计图像的梯度从输入图像或平滑版本的它。在这里分享一下Sobel算子的python实现。
Sobel算子,有时被称为Sobel–Feldman operator?或Sobel filter,用于图像处理和计算机视觉,特别是在边缘检测算法中,它创建强调边缘的图像。它是以斯坦福人工智能实验室(SAIL)的同事欧文·索贝尔(Irwin Sobel)和加里·费尔德曼(Gary Feldman)命名的。Sobel和Feldman在1968年SAIL的一次演讲中提出了“Isotropic?3?×?3 Image Gradient Operator”的概念从技术上讲,它是一个离散微分算子,计算图像强度函数梯度的近似。在图像中的每个点,Sobel Feldman算子的结果要么是对应的梯度向量,要么是这个向量的范数。Sobel Feldman算子是基于在水平和垂直方向上用一个小的、可分离的、整值滤波器对图像进行卷积,因此在计算方面相对便宜。另一方面,它产生的梯度近似是相对粗糙的,特别是在图像的高频变化。
Sobel算子使用两个3*3的kernel与原始图像卷积来计算导数的近似值,一个用于水平变化,一个用于垂直变化。如果我们定义I为源图像,Sx和Sy是两个3*3的kernel,计算如下:
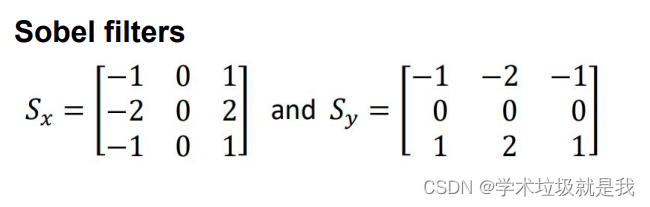
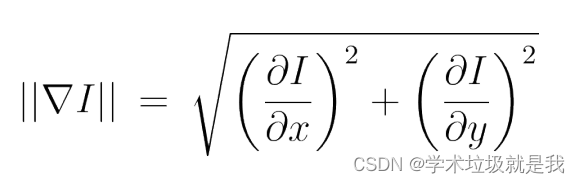
?代码实现 :
S_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
S_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])
imgCT = cv2.imread("CT.png", 0)
row_CT, col_CT = imgCT.shape
out_new_CT = np.zeros((row_CT, col_CT))
for r in range(row_CT - 2):
for c in range(col_CT - 2):
I_x = np.sum(np.multiply(imgCT[r:r+3, c:c+3], S_x))
I_y = np.sum(np.multiply(imgCT[r:r+3, c:c+3], S_y))
out_new_CT[r, c] = np.sqrt((I_x * I_x) + (I_y * I_y))
# 在写入最后结果的时候,为了边缘更加清晰一些
# 将大于200的像素值增加为255,图像会更加明显
if out_new_CT[r, c] > 200:
out_new_CT[r, c] = 255
plt.imshow(np.uint8(out_new_CT), cmap='gray')前后对比: