粒子滤波 PF——三维匀速运动CV目标跟踪(粒子滤波VS扩展卡尔曼滤波)
对于该博客跟踪代码以及问题探讨可以联系:WX:ZB823618313
对于其他跟踪定位问题的代码及探讨也可以联系
原创不易,路过的各位大佬请点个赞
粒子滤波 PF——三维匀速运动CV目标跟踪(粒子滤波VS扩展卡尔曼滤波)
一、问题描述(离散时间非线性系统描述)
考虑一般非线性系统模型,
x
k
=
f
(
x
k
?
1
,
w
k
?
1
)
z
k
=
h
(
x
k
,
v
k
)
(1)
x_k=f(x_{k-1},w_{k-1}) \\ z_k=h(x_k,v_k ) \tag{1}
xk?=f(xk?1?,wk?1?)zk?=h(xk?,vk?)(1)
其中
x
k
x_k
xk?为
k
k
k时刻的目标状态向量。
z
k
z_k
zk?为
k
k
k时刻量测向量(传感器数据)。这里不考虑控制器
u
k
u_k
uk?。
w
k
{w_k}
wk?和
v
k
{v_k}
vk?分别是过程噪声序列和量测噪声序列,并假设
w
k
w_k
wk?和
v
k
v_k
vk?为零均值高斯白噪声,其方差分别为
Q
k
Q_k
Qk?和
R
k
R_k
Rk?的高斯白噪声,即
w
k
~
(
0
,
Q
k
)
w_k\sim(0,Q_k)
wk?~(0,Qk?),
v
k
~
(
0
,
R
k
)
v_k\sim(0,R_k)
vk?~(0,Rk?),且满足如下关系(线性高斯假设)为:
E
[
w
i
v
j
′
]
=
0
E
[
w
i
w
j
′
]
=
0
i
≠
j
E
[
v
i
v
j
′
]
=
0
i
≠
j
\begin{aligned} E[w_iv_j'] &=0\\ E[w_iw_j'] &=0\quad i\neq j \\ E[v_iv_j'] &=0\quad i\neq j \end{aligned}
E[wi?vj′?]E[wi?wj′?]E[vi?vj′?]?=0=0i?=j=0i?=j?
二、贝叶斯滤波
定义
1
1
1 ~
k
k
k时刻对状态
x
k
x_k
xk?的所有测量数据为
z
k
=
[
z
1
T
,
z
2
T
,
?
?
,
z
k
T
]
T
z^k=[z_1^T,z_2^T,\cdots,z_k^T]^T
zk=[z1T?,z2T?,?,zkT?]T
贝叶斯滤波问题就是计算对 k k k时刻状态 x x x估计的置信程度,为此构造概率密度函数 p ( x k ∣ z k ) p(x_k |z^k) p(xk?∣zk),在给定初始分布 p ( x 0 ∣ z 0 ) = p ( x 0 ) p(x_0|z_0)= p(x_0) p(x0?∣z0?)=p(x0?)后,从理论上看,可以通过预测和更新两个步骤递推得到概率密度函数 p ( x k ∣ z k ) p(x_k |z^k) p(xk?∣zk)的值。
是不是卡尔曼滤波的雏形出现了,哈哈哈,预测、更新也存在KF中。
2.1、 预测
现假定
k
?
1
k- 1
k?1时刻的概率密度函数已知,则通过将Chapman-Kolmogorov等式应用
于动态方程(1),即可预测
k
k
k时刻状态的先验概率密度函数为
p
(
x
k
∣
z
k
?
1
)
=
∫
p
(
x
k
∣
x
k
?
1
)
p
(
k
?
1
∣
z
k
?
1
)
d
x
k
?
1
)
(2)
p(x_k |z^{k-1})=\int p(x_k |x_{k-1})p({k-1} |z^{k-1}) dx_{k-1}) \tag{2}
p(xk?∣zk?1)=∫p(xk?∣xk?1?)p(k?1∣zk?1)dxk?1?)(2)
实际上,状态转移方程写为概率密度的形式即为:
x
k
=
f
(
x
k
?
1
,
w
k
?
1
)
=
等价
p
(
x
k
∣
x
k
?
1
)
x_k=f(x_{k-1},w_{k-1}) \underset{\text{等价}}= p(x_k |x_{k-1})
xk?=f(xk?1?,wk?1?)等价=?p(xk?∣xk?1?)
式(2)中隐含假定了
p
(
x
k
∣
x
k
?
1
)
=
p
(
x
k
∣
x
k
?
1
,
z
k
?
1
)
p(x_k |x_{k-1})= p(x_k |x_{k-1}, z^{k-1})
p(xk?∣xk?1?)=p(xk?∣xk?1?,zk?1),实际上这本身在这里就是成立的,基于(1)式的马尔可夫过程。
2.2、 更新
在获得
p
(
x
k
∣
z
k
?
1
)
p(x_k |z^{k-1})
p(xk?∣zk?1)的基础上,结合
k
k
k时刻得到的新的量测值,基于贝叶斯公式,可以计算
k
k
k时刻状态的后验概率密度函数:
p
(
x
k
∣
z
k
)
=
p
(
z
k
∣
x
k
)
p
(
x
k
∣
z
k
?
1
)
p
(
z
k
∣
z
k
?
1
)
(3)
p(x_k |z^{k})=\frac{p(z_k |x_k)p(x_k |z^{k-1})}{p(z_k |z^{k-1})} \tag{3}
p(xk?∣zk)=p(zk?∣zk?1)p(zk?∣xk?)p(xk?∣zk?1)?(3)
式中分子
p
(
z
k
∣
z
k
?
1
)
p(z_k |z^{k-1})
p(zk?∣zk?1)有全概率公式得到
p
(
z
k
∣
z
k
?
1
)
=
∫
p
(
z
k
∣
x
k
)
p
(
x
k
∣
z
k
?
1
)
d
x
k
(4)
p(z_k |z^{k-1})=\int p(z_k |x_k)p(x_k |z^{k-1}) dx_{k} \tag{4}
p(zk?∣zk?1)=∫p(zk?∣xk?)p(xk?∣zk?1)dxk?(4)
我就说吧,上述过程实际上贝叶斯后燕推断的公式,哈哈哈哈啊哈
实际上这也是卡尔曼滤波的更新思想:在 k k k时刻得到测量 z k z_k zk?后,利用测量 z k z_k zk?修正先验概率,进而获得当前时刻状态的后验概率。我正是太机智了,哈哈啊哈
三、粒子滤波 PF(贝叶斯滤波的MC实现)
粒子滤波实际上是递推贝叶斯滤波的蒙特卡洛实现的一种算法,即一种近似的贝叶斯滤波。
核心思想:是使用一组具有相应权值的随机样本(粒子)来表示状态的后验分布。该方法的基本思路是选取一个重要性概率密度并从中进行随机抽样,得到一些带有相应权值的随机样本后,在状态观测的基础上调节权值的大小。和粒子的位置,再使用这些样本来逼近状态后验分布,最后将这组样本的加权求和作为状态的估计值。粒子滤波不受系统模型的线性和高斯假设约束,采用样本形式而不是函数形式对状态概率密度进行描述,使其不需要对状态变量的概率分布进行过多的约束,因而在非线性非高斯动态系统中广泛应用。尽管如此,粒子滤波目前仍存在计算量过大、粒子退化等关键问题亟待突破。
通常情况下选择先验分布作为重要性密度函数、即
q
(
x
k
∣
x
k
?
1
(
i
)
,
z
k
)
=
p
(
x
k
∣
x
k
?
1
(
i
)
)
q(x_k |x_{k-1}^{(i)}, z_{k})=p(x_k |x_{k-1}^{(i)})
q(xk?∣xk?1(i)?,zk?)=p(xk?∣xk?1(i)?)
对该函数取重要性权值为
w
k
(
i
)
=
w
k
?
1
(
i
)
p
(
z
k
∣
x
k
(
i
)
)
w_k^{(i)}=w_{k-1}^{(i)}p(z_k |x_{k}^{(i)})
wk(i)?=wk?1(i)?p(zk?∣xk(i)?)
同样
w
k
(
i
)
w_k^{(i)}
wk(i)?需要归一化得到
w
~
k
(
i
)
\tilde{w}_k^{(i)}
w~k(i)?。
标准的粒子滤波算法步骤为:
粒子滤波PF:
Step 1: 根据 p ( x 0 ) p(x_{0}) p(x0?)采样得到 N N N个粒子 x 0 ( i ) ~ p ( x 0 ) x_0^{(i)} \sim p(x_{0}) x0(i)?~p(x0?)
For i = 2 : N i=2:N i=2:N
??Step 2: 根据状态转移函数产生新的粒子为:$ x k ( i ) ~ p ( x k ∣ x k ? 1 ( i ) ) x_k^{(i)} \sim p(x_{k} |x_{k-1}^{(i)}) xk(i)?~p(xk?∣xk?1(i)?)
??Step 3: 计算重要性权值: w k ( i ) = w k ? 1 ( i ) p ( z k ∣ x k ( i ) ) w_k^{(i)}=w_{k-1}^{(i)}p(z_k |x_{k}^{(i)}) wk(i)?=wk?1(i)?p(zk?∣xk(i)?)
??Step 4: 归一化重要性权值: w ~ k ( i ) = w k ( i ) ∑ j = 1 N w k ( j ) \tilde{w}_k^{(i)}=\frac{w_k^{(i)}}{\sum_{j=1}^Nw_k^{(j)}} w~k(i)?=∑j=1N?wk(j)?wk(i)??
??Step 5: 使用重采样方法对粒子进行重采样(以随机重采样和系统重采样为例)
??Step 6: 得到 k k k时刻的后验状态估计:
E [ x ^ k ] = ∑ i = 1 N x k ( i ) w ~ k ( i ) E[\hat{x}_{k}]= \sum_{i=1}^Nx_{k}^{(i)}\tilde{w}_k^{(i)} E[x^k?]=i=1∑N?xk(i)?w~k(i)?
End For
算法:系统重采样 (systematic resampling)
For i = 1 : N i=1:N i=1:N
??Step 1: 初始化累积概率密度函数CDF: c 1 = 0 c_1=0 c1?=0
For i = 2 : N i=2:N i=2:N
??Step 2: 构造CDF: c i = c i ? 1 + w k ( i ) c_i=c_{i-1}+w_k^{(i)} ci?=ci?1?+wk(i)?
??Step 3: 从CDF的底部开始: i = 1 i=1 i=1
??Step 4: 采样起始点: u 1 = U [ 0 , 1 / N ] u_1=\mathcal{U}[0,1/N] u1?=U[0,1/N]
End For
For j = 1 : N j=1:N j=1:N
??Step 5: 沿CDF移动: u j = u 1 + ( j ? 1 ) / N u_j=u_{1}+(j-1)/N uj?=u1?+(j?1)/N
??Step 6: While u j > c i u_j>c_i uj?>ci?
?????? i = i + 1 i=i+1 i=i+1
?????End While
??Step 7: 赋值粒子: x k ( j ) = x k ( i ) x_k^{(j)}=x_k^{(i)} xk(j)?=xk(i)?
??Step 8: 赋值权值: w k ( j ) = 1 / N w_k^{(j)}=1/N wk(j)?=1/N
??Step 9: 赋值父代: i ( j ) = i i^{(j)}=i i(j)=i
End For
四、仿真场景:三维雷达目标跟踪
4.1 仿真场景(三维匀速目标)
目标模型
考虑一各三维的匀速运动目标(CV 模型):
x
k
+
1
=
F
k
x
k
+
G
k
w
k
x_{k+1}=F_kx_k+G _kw_k
xk+1?=Fk?xk?+Gk?wk?
其中状态向量
x
k
=
[
x
k
,
x
˙
k
,
y
k
,
y
˙
k
,
z
k
,
z
˙
k
]
′
x_k=[x_k,\dot{x}_k,y_k,\dot{y}_k,z_k,\dot{z}_k]'
xk?=[xk?,x˙k?,yk?,y˙?k?,zk?,z˙k?]′;噪声为
w
k
=
[
w
x
,
w
y
,
w
z
]
′
w_k=[w_x,w_y,w_z]'
wk?=[wx?,wy?,wz?]′;状态转移矩阵
F
k
F_k
Fk?和噪声驱动矩阵
G
k
G_k
Gk?如下
F
k
=
[
1
T
0
0
0
0
0
1
0
0
0
0
0
0
1
T
0
0
0
0
0
1
0
0
0
0
0
0
1
T
0
0
0
0
0
1
]
Γ
k
=
[
1
/
2
T
2
0
0
T
0
0
0
1
/
2
T
2
0
0
T
0
0
1
/
2
T
2
0
0
T
]
F_k=\begin{bmatrix}1 & T & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 0 \\0 & 0 & 1 & T & 0 & 0\\0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 0 & 1 & T\\0 & 0 & 0 & 0 & 0 & 1\end{bmatrix} \qquad\varGamma_k=\begin{bmatrix}1/2T^2 & 0 & 0 \\T & 0 & 0 \\0 & 1/2T^2 & 0 \\0 & T & \\0 & 0 & 1/2T^2 \\0 & 0 & T\end{bmatrix}
Fk?=?????????100000?T10000?001000?00T100?000010?0000T1??????????Γk?=?????????1/2T2T0000?001/2T2T00?0001/2T2T??????????
采样时间
T
=
1
s
T=1s
T=1s. 初始状态为
x
0
~
(
x
ˉ
0
,
P
0
)
x
ˉ
0
=
[
1
km
,
20
m/s
,
1
km
,
20
m/s
,
1
km
,
20
m/s
]
′
P
0
=
diag
(
1
0
5
m
2
,
1
0
2
m
2
/
s
2
,
1
0
5
m
2
,
1
0
2
m
2
/
s
2
,
1
0
5
m
2
,
1
0
2
m
2
/
s
2
)
x_0\sim(\bar{x}_0,P_0)\\\bar{x}_{0}=[1\text{km}, 20\text{m/s} ,1\text{km}, 20\text{m/s} ,1\text{km}, 20\text{m/s}]'\\P_{0}=\text{diag}(10^5\text{m}^2, 10^2\text{m}^2/\text{s}^2, 10^5\text{m}^2, 10^2\text{m}^2/\text{s}^2, 10^5\text{m}^2, 10^2\text{m}^2/\text{s}^2)
x0?~(xˉ0?,P0?)xˉ0?=[1km,20m/s,1km,20m/s,1km,20m/s]′P0?=diag(105m2,102m2/s2,105m2,102m2/s2,105m2,102m2/s2)
过程噪声均值和方差分别为
q
=
10
q=10
q=10
w
ˉ
k
=
[
0
,
0
,
0
]
′
Q
k
=
[
q
2
0
0
0
q
2
0
0
0
q
2
]
\bar{w}_k=[0,0, 0]'\\Q_k=\begin{bmatrix}q^2 & 0& 0 \\0 & q^2 & 0\\0&0 & q^2 \end{bmatrix}
wˉk?=[0,0,0]′Qk?=???q200?0q20?00q2????
如果为非线性目标,则将状态转移矩阵 F k F_k Fk?代替为雅可比矩阵即可。为了不是一般性这里采用线性模型进行仿真。主要处理目标跟踪,雷达量测存在的非线性滤波问题。
雷达量测模型
在三维情况下,雷达量测为距离和角度
r
k
m
=
r
k
+
r
~
k
b
k
m
=
b
k
+
b
~
k
e
k
m
=
e
k
+
e
~
k
{r}_k^m=r_k+\tilde{r}_k\\ b^m_k=b_k+\tilde{b}_k\\ e^m_k=e_k+\tilde{e}_k
rkm?=rk?+r~k?bkm?=bk?+b~k?ekm?=ek?+e~k?
其中
r
k
=
(
x
k
?
x
0
)
+
(
y
k
?
y
0
)
2
)
b
k
=
tan
?
?
1
y
k
?
y
0
x
k
?
x
0
e
k
=
tan
?
?
1
z
k
?
z
0
(
x
k
?
x
0
)
2
+
(
y
k
?
y
0
)
2
r_k=\sqrt{(x_k-x_0)^+(y_k-y_0)^2)}\\ b_k=\tan^{-1}{\frac{y_k-y_0}{x_k-x_0}}\\ e_k=\tan^{-1}{\frac{z_k-z_0}{\sqrt{(x_k-x_0)^2+(y_k-y_0)^2}}}\\
rk?=(xk??x0?)+(yk??y0?)2)?bk?=tan?1xk??x0?yk??y0??ek?=tan?1(xk??x0?)2+(yk??y0?)2?zk??z0??
[
x
0
,
y
0
,
z
0
]
[x_0,y_0,z_0]
[x0?,y0?,z0?]为雷达坐标,一般情况为0。雷达量测为
z
k
=
[
r
k
,
b
k
,
e
k
]
′
z_k=[r_k,b_k,e_k]'
zk?=[rk?,bk?,ek?]′。雷达量测方差为
R
k
=
cov
(
v
k
)
=
[
σ
r
2
0
0
0
σ
b
2
0
0
0
σ
e
2
]
R_k=\text{cov}(v_k)=\begin{bmatrix}\sigma_r^2 & 0 &0\\0 & \sigma_b^2 &0\\0&0& \sigma_e^2 \end{bmatrix}
Rk?=cov(vk?)=???σr2?00?0σb2?0?00σe2?????且
σ
r
=
20
m
\sigma_r=20m
σr?=20m,
σ
b
=
20
m
r
a
d
\sigma_b=20mrad
σb?=20mrad,
σ
e
=
15
m
r
a
d
\sigma_e=15mrad
σe?=15mrad。
4.2 跟踪轨迹
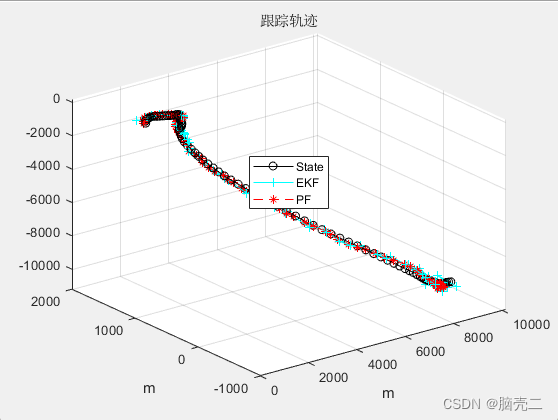
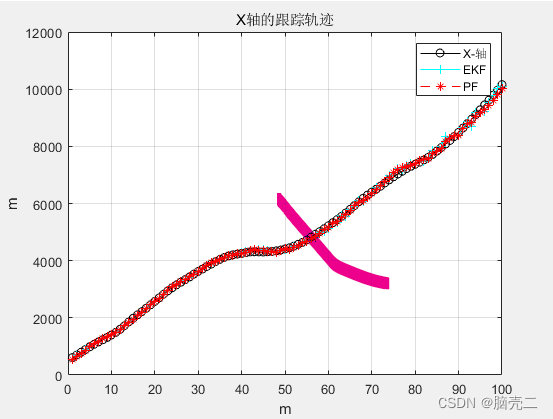
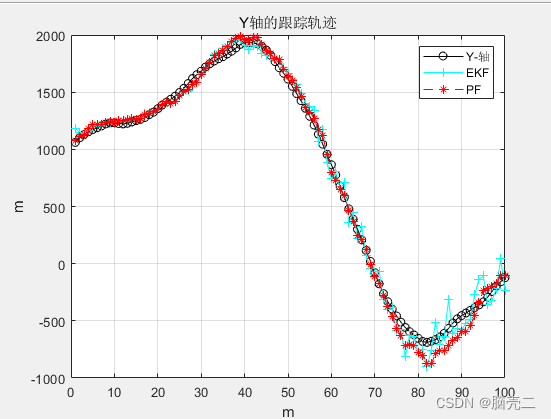
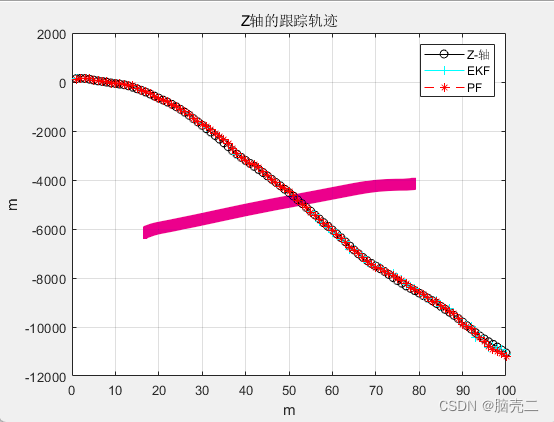
4.3 跟踪误差
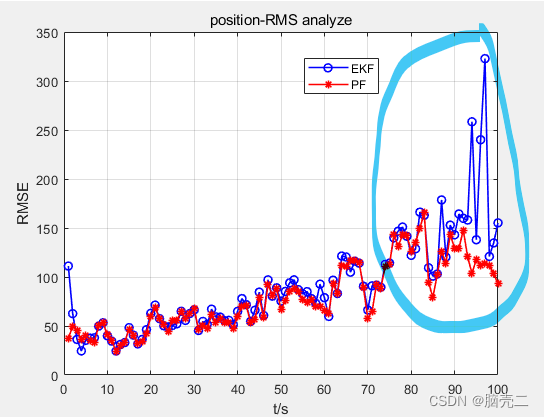
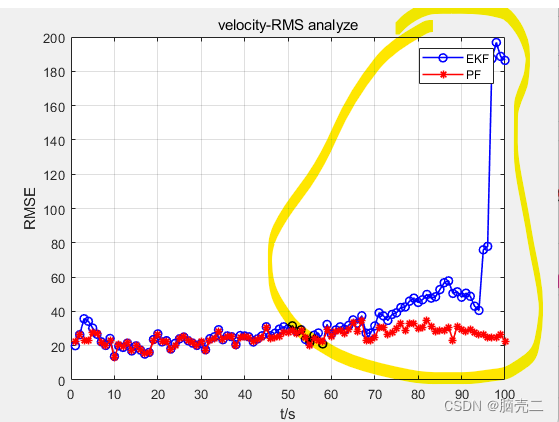
五、部分代码
对于该博客跟踪代码以及问题探讨可以联系:WX:ZB823618313
对于其他跟踪定位问题的代码及探讨也可以联系
5.1、主函数部分代码
clear all; close all; clc;
%% initial parameter
n=6; %状态维数 ;
T=1; %采样时间
M=1; %雷达数目
N=100; %运行总时刻
MC=10; %蒙特卡洛次数
global N_pf
N_pf=5000;% 采样点数PF
chan=1; %滤波器通道,这里只有一个滤波器
w_mu=[0,0,0]';% mean of process noise
v_mu=[0,0,0]';% mean of measurement noise
%% target model
%covariance of process noise
q=10; %m/s^2
Qk=q^2*eye(3);
% state matrix
% CV
Fk=[1,T,0,0,0,0;
0,1,0,0,0,0;
0,0,1,T,0,0;
0,0,0,1,0,0;
0,0,0,0,1,T;
0,0,0,0,0,1 ];
Gk=[ T^2/2, 0, 0;
T, 0, 0;
0,T^2/2, 0;
0, T, 0;
0, 0,T^2/2;
0, 0, T ];
%量测模型
sigma_r(1)=20; sigma_b(1)=20e-3; sigma_e(1)=15e-3; % covariance of measurement noise (radar)
% sigma_r=300; sigma_b=200e-3; sigma_e=100e-3;
Rk=diag([sigma_r(1)^2, sigma_b(1)^2,sigma_e(1)^2]);
xp=[0,0,0,0,0,0];%雷达位置
%% 定义存储空间
sV=zeros(n,N,MC); % 状态
eV=zeros(n,N,MC,chan); %估计
PV=zeros(n,n,N,MC,chan);%协方差
rV=zeros(3,N,MC,M); % %量测
for i=1:MC
sprintf('rate of process:%3.1f%%',(2*i)/(4*MC)*100)
% 初始状态的均值和方差
x=[1000,500,1000,0,100,100]';
P_0=diag([1e4,10^2,1e4,10^2, 1e4,10^2]);
x=[1000,80,1000,50,100,10]';
P_0=diag([1e5,10^2,1e5,10^2, 1e5,10^2]);
% x=[100,50,100,50,100,50]';
% P_0=diag([5e5,1e3,5e5,1e3,5e5,1e3]); %initial covariance
xk_EKF=x; Pk_EKF=P_0; % P0|0 x0|0
xk_pf=x; Pk_pf=P_0; % P0|0 x0|0
%产生N个粒子
for ii = 1 : N_pf
xpart(:,ii) = x+ sqrtm(P_0) * randn(6,1);
end
5.2、PF部分代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%函数功能:实现随机重采样算法
%输入参数:weight为原始数据对应的权重大小
%输出参数:outIndex是根据weight对inIndex筛选和复制结果
function outIndex=randomR(weight)
%获得数据的长度
L=length(weight);
%初始化输出索引向量,长度与输入索引向量相等
outIndex=zeros(1,L);
%第一步:产生[0,1]上均匀分布的随机数组,并升序排序
u=unifrnd(0,1,1,L);
u=sort(u);
%u=(1:L)/L%这个是完全均匀
%第二步:计算粒子权重积累函数cdf
cdf=cumsum(weight);
%第三步:核心计算
i=1;
for j=1:L
%此处的基本原理是:u是均匀的,必然是权值大的地方
%有更多的随机数落入该区间,因此会被多次复制
while(i<=L)&(u(i)<=cdf(j))
%复制权值大的粒子
outIndex(i)=j;
%继续考察下一个随机数,看它落在哪个区间
i=i+1;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 系统重采样子函数
% 输入参数:weight为原始数据对应的权重大小
% 输出参数:outIndex是根据weight筛选和复制结果
function outIndex = systematicR(weight);
N=length(weight);
N_children=zeros(1,N);
label=zeros(1,N);
label=1:1:N;
s=1/N;
auxw=0;
auxl=0;
li=0;
T=s*rand(1);
j=1;
Q=0;
i=0;
u=rand(1,N);
while (T<1)
if (Q>T)
T=T+s;
N_children(1,li)=N_children(1,li)+1;
else
i=fix((N-j+1)*u(1,j))+j;
auxw=weight(1,i);
li=label(1,i);
Q=Q+auxw;
weight(1,i)=weight(1,j);
label(1,i)=label(1,j);
j=j+1;
end
end
index=1;
for i=1:N
if (N_children(1,i)>0)
for j=index:index+N_children(1,i)-1
outIndex(j) = i;
end;
end;
index= index+N_children(1,i);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%