[人工智能]论文阅读--Multi-Attention Multiple Instance Learning

注意力机制背后的最初想法是取代简单的平均输出
简单的平均输出：$y^{?}=n^{?1}\sum _{i=1}^n{y}_i$
引入回归模型后对$x$的标签的预测值为：
$$y^{?}=\sum _{i=1}^n\alpha (x,x_i)y_i$$
其中的加权为：$\alpha (x,x_i)$表示$x_i$和$x$的相关性，$x_i$属于训练集的向量，$y_i$表示训练向量的对应标签。

权重的原始形式之一是由核K定义的，它可以被视为一个得分函数，估计向量$x_i$和$x$的相关性。权重公式如下：
$$\alpha (x,x_i)=\frac{K(x,x_i)}{{\sum }_{j=1}^{n}K(x,x_j)}$$

开局一张图

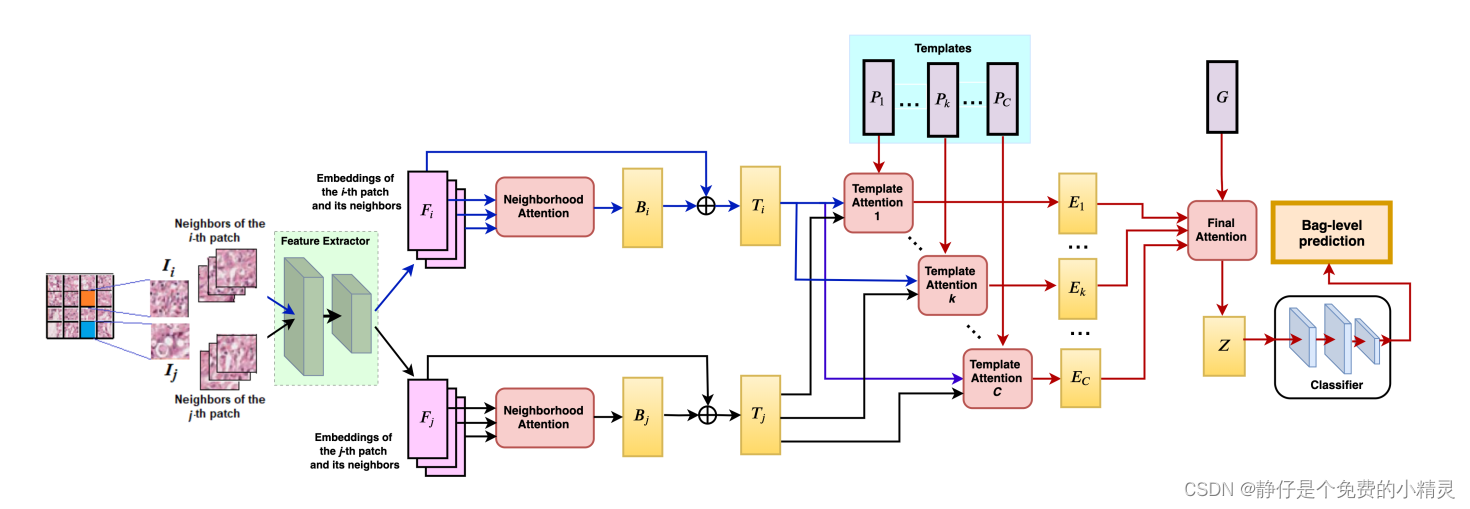
• 最左边的图片表示一个包，其中的每一个小块表示包中的每一个实例，假设其中有$m$个实例，使用两个不同颜色的高亮色块表示第$i$个实例$I_i$和第$j$个实例$I_j$。

• 所有小块(实例)都被输入经过训练的神经网络，使用一维卷积计算其嵌入$F_i$，目的是降低实例$I_i$的维度：
  $$F_i=Conv(I_i),i=1,\dots ,m.$$

• 我们使用$(x_i,y_i)$表示在整个图像中第$i$个小块的坐标。
  使用 M = { 1 , … , m } \mathcal{M}=\{1,\dots,m\} M={1,…,m}表示整幅图像中所有小块的索引集。
  第$i$个小块的邻居的索引集${\mathcal{N}}_i?\mathcal{M}$为:
  N = { j ∈ M ∣ 0 < max ? ( ∣ x i ? x j ∣ , ∣ y i ? y j ∣ ) ≤ d } \mathcal{N}=\{j\in \mathcal{M}|0<\max(|x_i-x_j|,|y_i-y_j|)\leq d\} N={j∈M∣0<max(∣xi??xj?∣,∣yi??yj?∣)≤d}
  $d$可以是任意值，在本实验中$d$的取值为1。并且值得注意的是，邻居是在包内找的。

• 邻居的使用可以改善分类结果，这里我们引入注意机制，计算$I_i$的邻居联合嵌入$B_i$为：
  $$B_i=\sum _{j\in {\mathcal{N}}_i}{\alpha }_j^{(i)}{F}_j$$

• 根据第实例$I_i$的第$j$个邻居的权重${\alpha }_j^{(i)}$
  $${\alpha }_j^{(i)}=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}(s^{(i)})=\frac{exp(s_j^{(i)})}{{\sum }_{t}exp(s_t^{(i)})}$$
  其中$s_j^{(i)}$是将两个向量$F_i$和$F_j$映射到标量的注意力评分函数:
  $$s_j^{(i)}={\mathbf{s}\mathbf{c}\mathbf{o}\mathbf{r}\mathbf{e}}_{nb}(F_i,F_j)=F^{T}tanh(V_{nb}{F}_j)$$
  其中$V$是可学习参数的矩阵

• 总之，我们为每个$F_i$得到一个嵌入$B_i$，$B_i$中包含了关于邻居的信息。将第$i$个实例的嵌入与邻域$B_i$的联合嵌入串联起来，得到嵌入$T_i$:
  $$T_i=(F_i,B_j)$$
  串联操作在图中用符号⊕表示. 现在每个包都由一组嵌入向量$T_i$表示。

该算法提出的另一个重要概念是一组嵌入模板，这些模板被视为可学习向量。此外，模板数量是$C$，其值决定分类质量。模板可以被视为应用于嵌入$T_i$集的多重关注的实现。由于神经网络的初始化规则不同，它们是不同的网络。？？？？
使用$\mathcal{P}=P_1,\dots ,P_C$表示模板的集合,然后，每个模板产生相应的聚合嵌入$E_k$：
$$E_k=\sum _{i=1}^m{\beta }_k^{(k)}{T}_i,k=1,\dots ,C$$

其中：这个公式不懂没有说score是怎么算的
$${\beta }_k^{(k)}=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}(?score(P_k,T_i){?}_i)$$

这里引入softmax进行归一化操作，第$k$个聚合嵌入$E_k$是图像中具有邻域的所有小块（实例）嵌入的加权平均值，其权重由第$k$个模板定义。换句话说，第$k$个聚集嵌入相对于第$k$个模板对整个图像或包进行特征化。有关所有面片及其相邻面片的信息包含在$C$个向量$E_1,\dots ,E_C$中。

• 与所有$C$个模板相对应的聚合嵌入$E_k$被分组到与整个图像或袋子和所有模板相对应的总向量$Z$中,$Z$是包最后被映射为的向量。
  $$Z=\sum _{k=1}^C{\gamma }_k{E}_k$$
  其中：
  $${\gamma }_k=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}(?score(G,E_k){?}_k)$$
  $G$是训练向量的全局模板。
  ，模板$G$和相应的最终注意 final attention决定了哪些聚合嵌入$E_k$和模板$P_k$是重要的，并且，在分类器之前使用注意机制可以使得模型具有可解释性。

建议使用带有参数$\theta$的分类层$g_{\theta }(Z)$，该参数定义了包级别（整个图像级别）上分类标签为1的概率。

上述描述了处理$I_i$的步骤，真正的实现假设以相同的方式处理包的所有$I$。

整个神经网络使用随机梯度下降和Adam优化器进行端到端的训练。在每个步骤中，从训练集中选择一个图像（一个包），然后将其划分为多个面片。这些面片被用作神经网络的输入。使用神经网络的结果是对一类概率的估计，例如，这意味着图像是否包含恶性细胞。根据得到的估计和整个图像标签确定损失函数。为了更新神经网络权重，使用自动微分算法为每个训练参数确定损失函数的偏导数值。然后以标准方式更新训练参数值。

损失函数：

$$L=\frac{1}{N}\sum _{k=1}^{N}BCE(Y_k,f(X_k))+\frac{2}{C(C?1)}\sum _{i<j}(P_i^T?P_j{)}^2$$

这里的第一项是标准二分类交叉熵（BCE）损失函数；$f(X_k)$是整个神经网络的输出。$Y_k$是真实标签

BCE损失函数： $$loss(x,y)=?[y\log x+(1?y)\log (1?x)]$$ 其中$x$是模型输出，$y$是真实标签。

在第二项中，当$P_i$和$P_j$的差距越大时，损失就越小，因此损失函数中的第二项旨在使得$P_i$和$P_j$尽可能不同。

计算包中实例的重要性

根据上述的步骤，一个包最终被映射成了一个向量的表示：$Z=\sum _{k=1}^C{\gamma }_k{E}_k$
可以通过如下公式推导出：

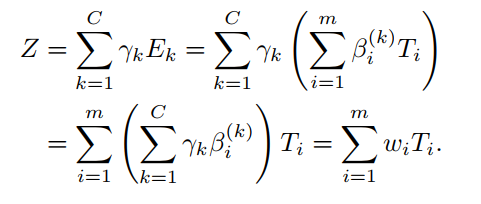
在这里可以把$w_i={\sum }_{k=1}^C{\gamma }_k{\beta }_i^{(k)}$看作是实例$I_i$在它的邻居中的重要性。并且${\sum }_{i=1}^m{w}_i=1$,包中所有的实例的重要性之和为$1$。

注意！前面已经提到过，第实例$I_i$的第$j$个邻居的重要性为${\alpha }_j^{(i)}$。因此我们可以考虑将实例邻居的重要性和实例本身的重要性联系起来。
如果我们假设向量$T_i$的所有元素都是等价的，那么它的两部分的重要性度量是相等的。但是，如果指数为$i$和$j$的图像小块是相邻的，则$B_i$的值可能会与$T_j$有关联。因此我们定义第$i$个图像小块的最终重要性$v_i$为：
$$v_i=w_i+\sum _{j\in N_i}{\alpha }_j^{(i)}{w}_j$$