支持向量机
SVM(Support Vector Machines,支持向量机)是核变换技术的代表算法之一,是一种具有精度高、运算速度快、泛化能力强等优点的统计学习新算法,其主要思想是将低维空间中的线性不可分问题,经过核变换处理,转换到高维空间,实现准确分类,遥感数据的处理方法中时常见到SVM的身影。其目标是寻找可以准确地将两个类别划分开,并同时使边际(margin)最大的超平面(hyper plane),超平面的定义公式是W^T X+b=0,其中W代表权重向量、X是训练实例、b是bias偏向。SVM最早是由Vladimir N等在1963年提出的,此后得到快速发展并衍生出硬边距的线性SVM(1964年)和软边距的非线性SVM(1995年)。
1 SVM基本概念
分类问题是机器学习的一大任务。如图1展示的是一个二分类问题,图中的黑心点和空心点,事先被标记为两类。SVM的目标是找到一个将其“完美”分类的超平面。
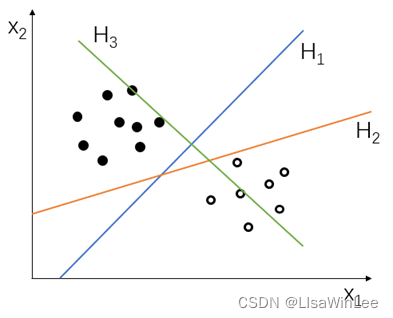
图1 二分类问题示意图
图1所示的二分类问题是可以找到很多个超平面将两个类别分开的,如图1中H1和H2。为了确定一个“完美”分类的超平面,而又没有办法将真实世界中的所有数据都参与测试,因此,在SVM中,提出假设:使 “间隔”最大的超平面就是 “完美”分类,最后建立模型去验证这个假设。这就是SVM的核心思想,即寻找一个使其间隔最大的超平面。
“间隔”的意思是所有数据点中到超平面的最小距离。如图2所示,H1为超平面,H2和H3为间隔边界,黑色箭头为间隔,即虚线上的点到超平面的距离。图中的红点到超平面的距离最小,是这四个点共同决定了超平面的位置,因此它们被称为“支持向量”,“支持向量机”由此而得名。
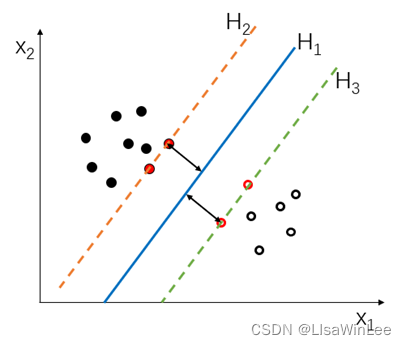
图2.3 SVM的核心思想演示图
2 线性可分性
给定一组数据{(χ_1,y_1 ),(χ_2,y_2 ),…,(χ_m,y_m )} ,其中x_i=[x_1,…,x_n]∈x ,y∈{-1,1}。若输入数据线性可分,即两类样本数据按正类和负类可以被一个超平面w^T?x+b=0线性分开,并且每一个样本数据点到平面的距离都大于等于1:y_i (w^T?x_i+b)≥1,则称该分类问题具有线性可分性,参数w,b分别表示超平面的法向量和截距。
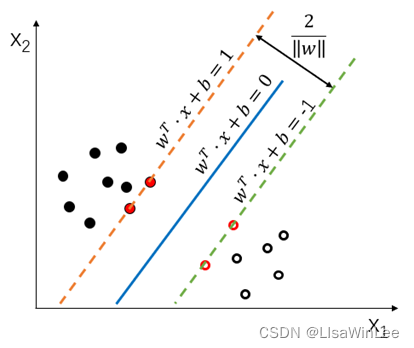
图3 SVM 的线性可分性演示图
判别样本分类的间隔边界由两个平行的超平面来表示:
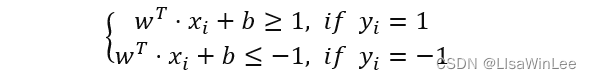
上间隔边界的上方是正类样本,下间隔边界下方是负类样本。它们之间的距离d=2min |w^T?x+b|/‖w‖ =2/‖w‖ 叫做边距,被间隔边界线穿过的所有样本点都是SVM的支持向量。
线性SVM的优化目标即为:
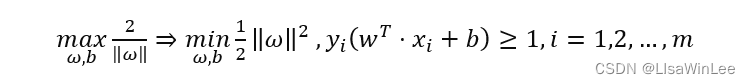
3 损失函数
现实生活中,具有线性可分性的实际问题并不是很多,如果继续使用超平面做决策边界会造成一定的分类损失。因为在线性分类中,会存在部分样本点处在两个间隔边界的中间,或者进入到其他分类区域。损失函数就是用来表示产生的分类损失的,按照数学表达的形式可以是0-1损失函数:
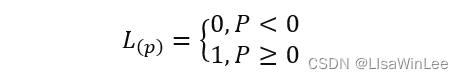
因为0-1损失函数不是连续函数,为了问题求解的优化,因此通常会构造代理损失。包括铰链损失函数、logistic损失函数和指数损失函数,SVM中用到的是铰链损失函数:
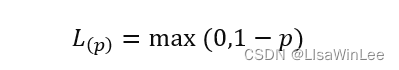
4 核方法
现实生活中大多数的分类问题都是非线性问题,无法用超平面解决,所以在此引入核函数,构建非线性SVM。如下图4所示,是使用多项式核函数和高斯核函数的SVM模型示意图,两种核函数都能很好的将样本分类。
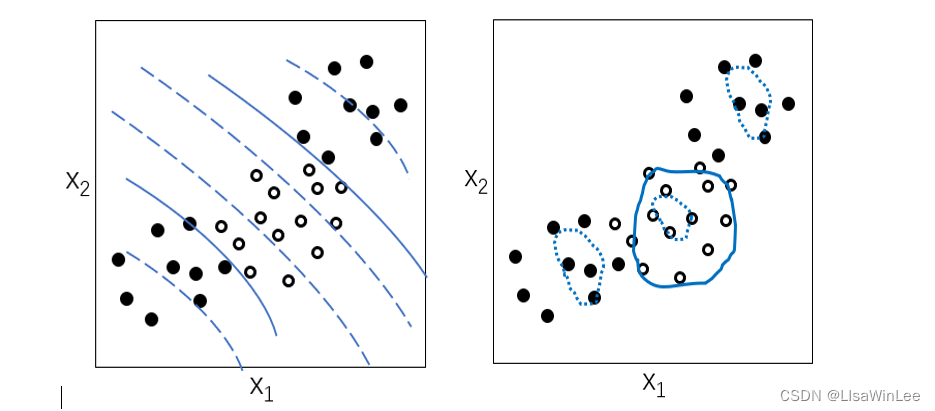
图4 多项式核函数(左)和高斯核函数(右)分类示意图
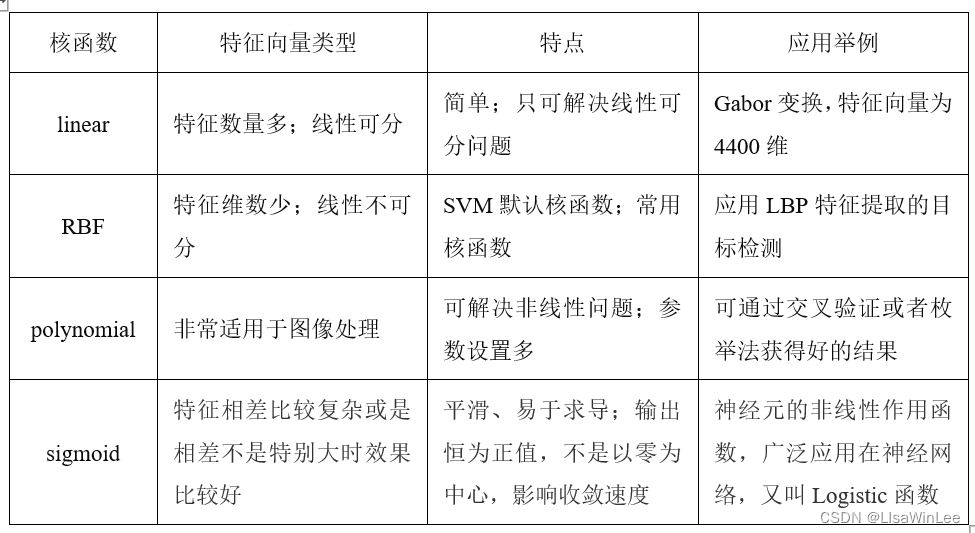
核函数的选用是应用SVM的关键,一般在图像处理方面常用的核函数有四个:linear(线性核),RBF(高斯核函数),polynomial(多项式核),sigmoid核函数,如表1所示。
表1 四个核函数的选用比较
sklearn.svm包中的SVC(kernel=”linear“)和LinearSVC的区别
参考:https://stackoverflow.com/questions/45384185/what-is-the-difference-between-linearsvc-and-svckernel-linear
1、LinearSVC使用的是平方hinge loss,SVC使用的是绝对值hinge loss
(我们知道,绝对值hinge loss是非凸的,因而你不能用GD去优化,而平方hinge loss可以)
2、多分类策略:LinearSVC使用的是One-vs-All(也成One-vs-Rest),而SVC使用的是One-vs-One
3、多分类策略决定模型个数:如果分类的数量是N,则LinearSVC适合N模型,而SVC适合N(N-1)/2模型
4、对于二分类问题一般只有其中一个合适,具体问题具体对待
5、LinearSVC基于liblinear,罚函数是对截矩进行惩罚;SVC基于libsvm,罚函数不是对截矩进行惩罚。
6、我们知道SVM解决问题时,问题是分为线性可分和线性不可分问题的,liblinear对线性可分问题做了优化,故在大量数据上收敛速度比libsvm快
(一句话,大规模线性可分问题上LinearSVC更快)
调参
validation_curve: 展示某一个因子,不同取值的算法的得分
通过这种曲线可以更加直观看出改变模型中的参数,有没有出现过拟合
validation_curve(estimator, X, y, param_name, param_range, groups=None, cv=None, scoring=None, n_jobs=1, pre_dispatch=‘all’, verbose=0)
estimator:实现了fit 和 predict 方法的对象
X : 训练的向量
y : 目标相对于X分类或回归
param_name:将被改变的变量名称
param_range:param_name对应的变量的取值
cv:如果传入整数,测试数据将分成对应的分数,其中一份作为cv集,其余n-1作为traning(默认为3份)
scoring文档:https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter