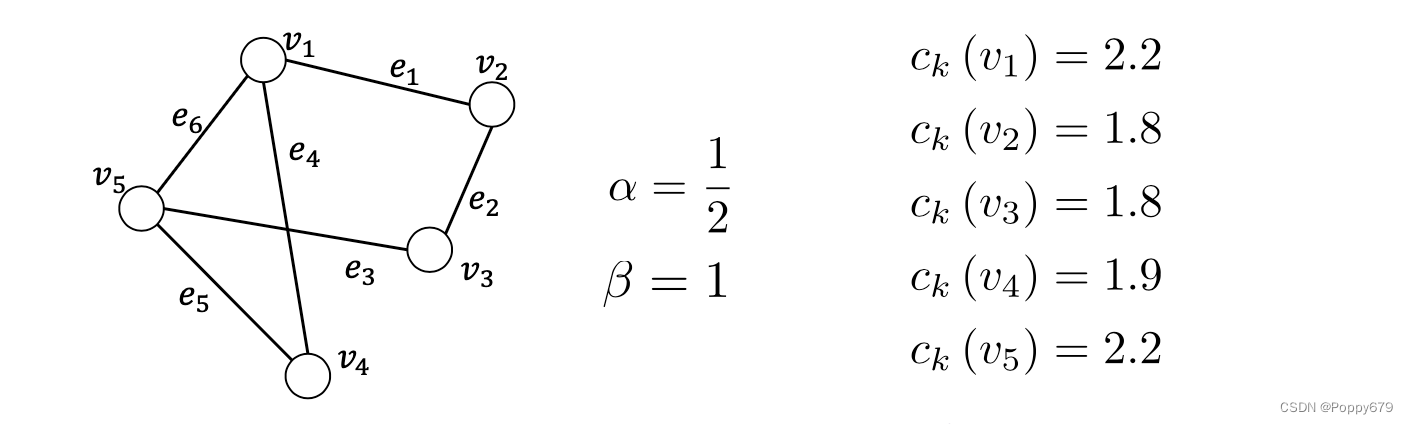图论基础
简介
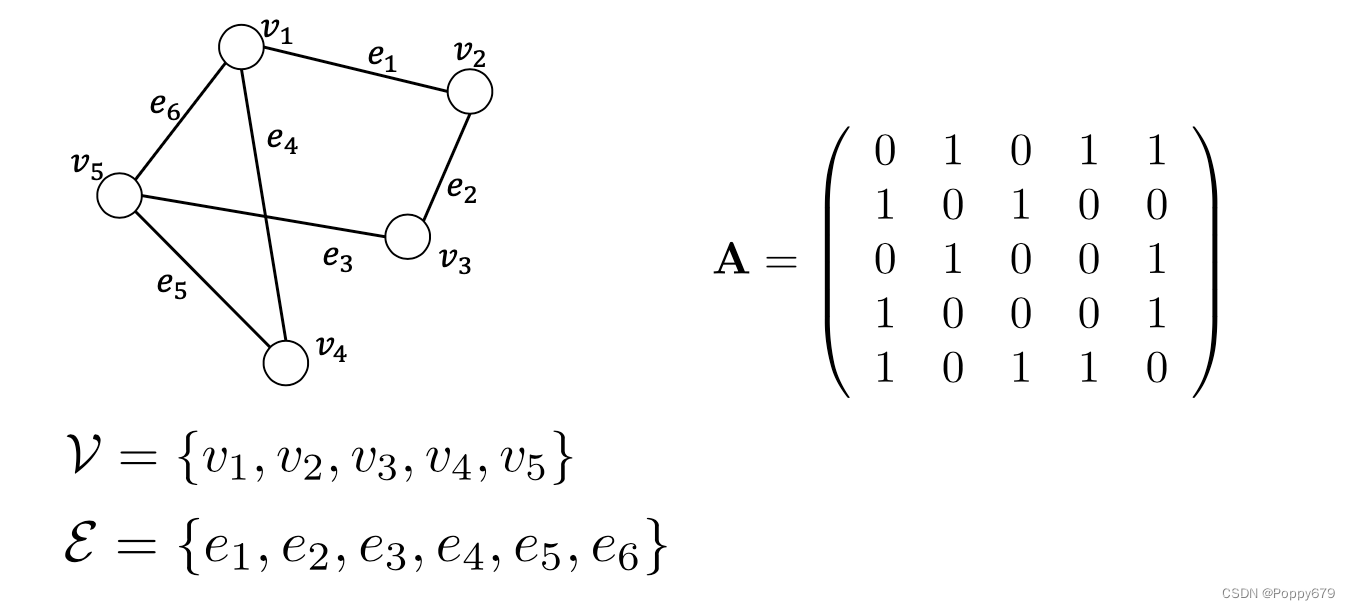
边描述两节点的关系,上图为无向图。图可以通过邻接矩阵来表示,若节点1到节点2之间存在边,那么邻接矩阵的第一行的第二列为1,第二行的第一列也为1。因为无向图的表示应该是双向的。
图的性质
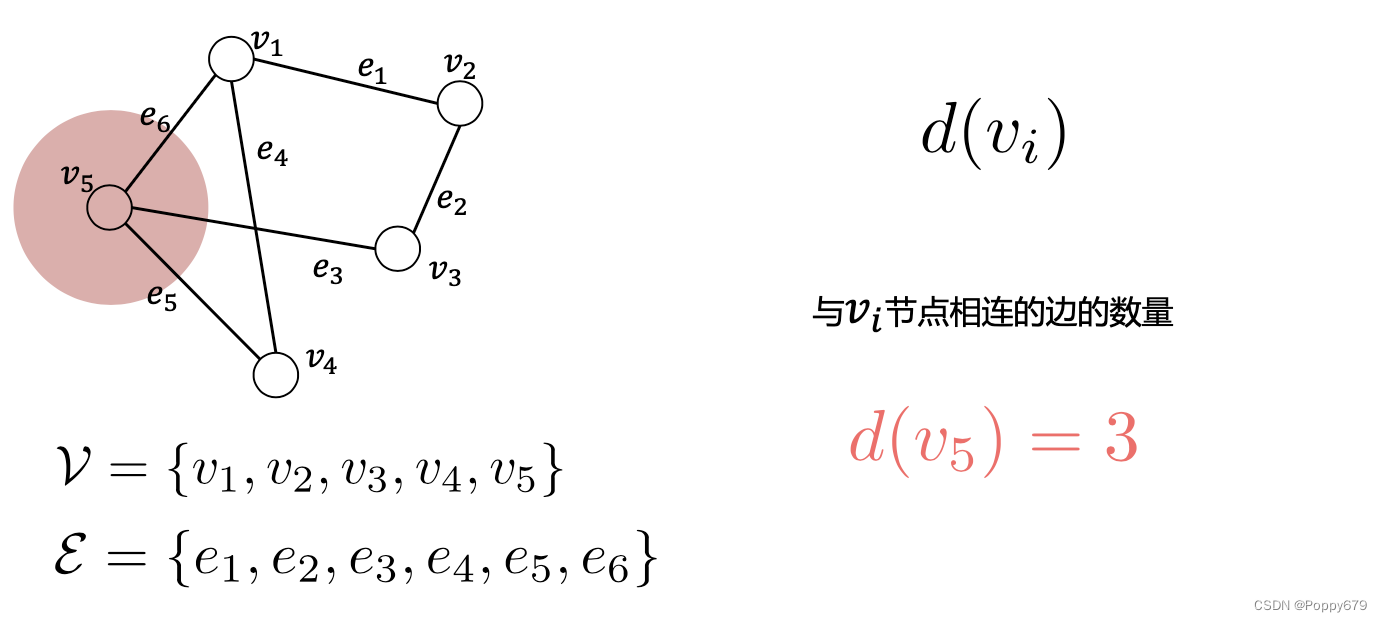
度 d ( v i ) d(v_i) d(vi?):与节点 v i v_i vi?相连的边的数量
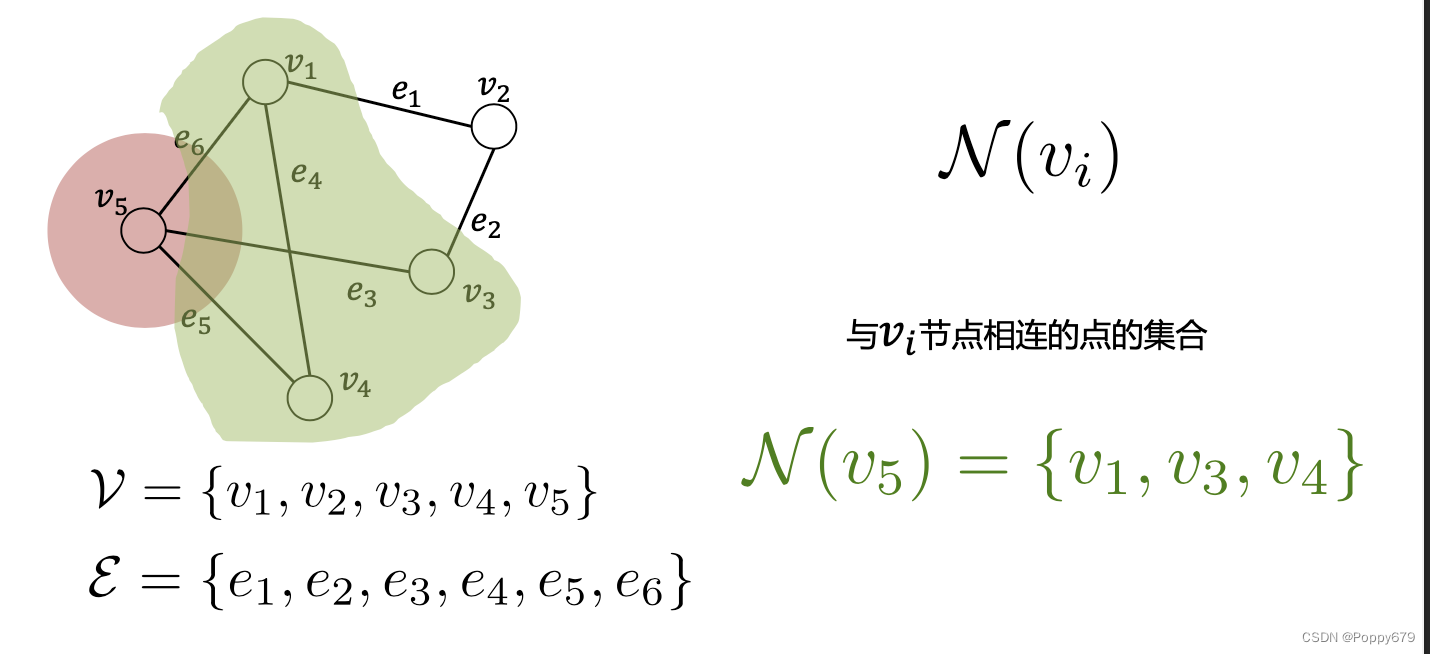
节点的邻域
邻域
N
(
v
i
)
N(v_i)
N(vi?):与节点
v
i
v_i
vi?相连的节点的集合
途径Walk
途径是节点和边交替的序列,从一个节点开始,以一个节点结束,其中每条边与紧邻的节点相连。
途径的长度:途径中包含的边的数量
两种特殊的途径:
trail迹:边各不相同的途径
path路:节点各不相同的途径

连通图
给定一个图,如果图中的任意两个节点之间都至少存在一条路,则这个图是一个连通图。
最短路:给定连通图中的任意两点,连接着两点的长度最小的路(经过的边个数最少)被称为这两个点之间的最短路。最短路的长度被称为两点之间的距离。
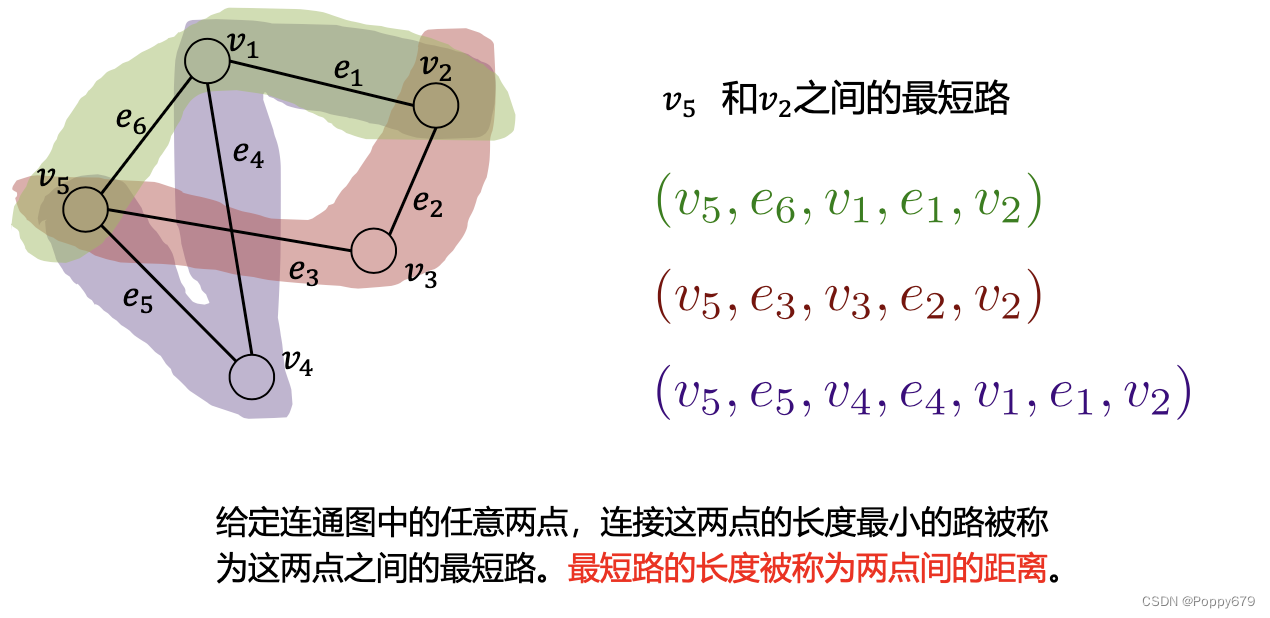
图的直径:图中最远的两点间的距离(最长的最短路的边的个数?)
节点中心性
节点的中心行用来衡量节点在图上的重要程度
将每个节点映射到一个标量,那么每个节点对应一个分数。这个分数就可以用来衡量节点在图中的重要性。
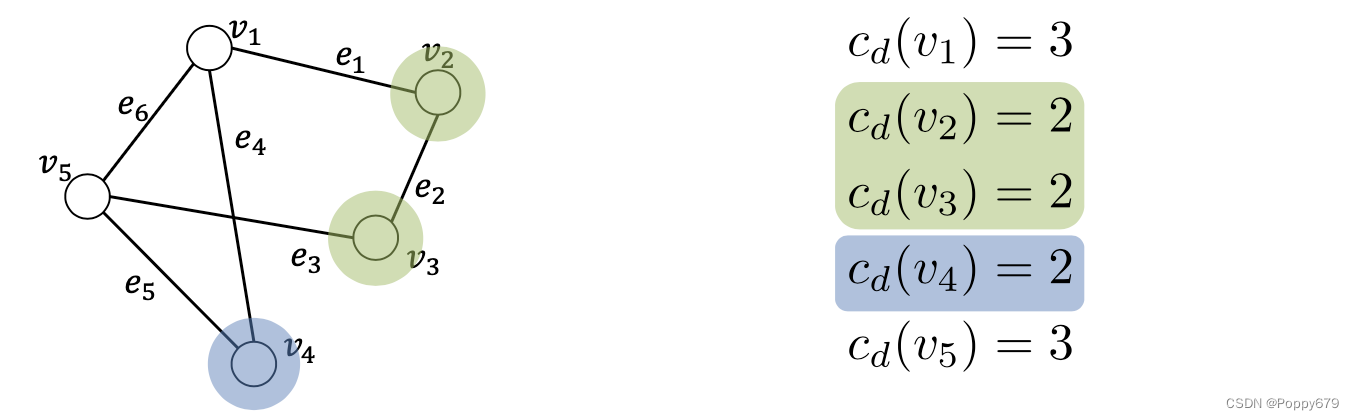
度中心性
利用节点的度来衡量节点的中心性,度越高就认为其更重要,但是比如在社将网络中,你有很多粉丝但都是僵尸粉,相比粉丝没有那么多,但都是优质粉丝的用户来说,你就没有那么重要。因此,单纯度中心性不能很好的衡量节点中心性。
c
d
(
v
i
)
=
d
(
v
i
)
=
∑
j
=
1
N
A
i
,
j
c_{d}\left(v_{i}\right)=d\left(v_{i}\right)=\sum_{j=1}^{N} \mathbf{A}_{i, j}
cd?(vi?)=d(vi?)=∑j=1N?Ai,j?
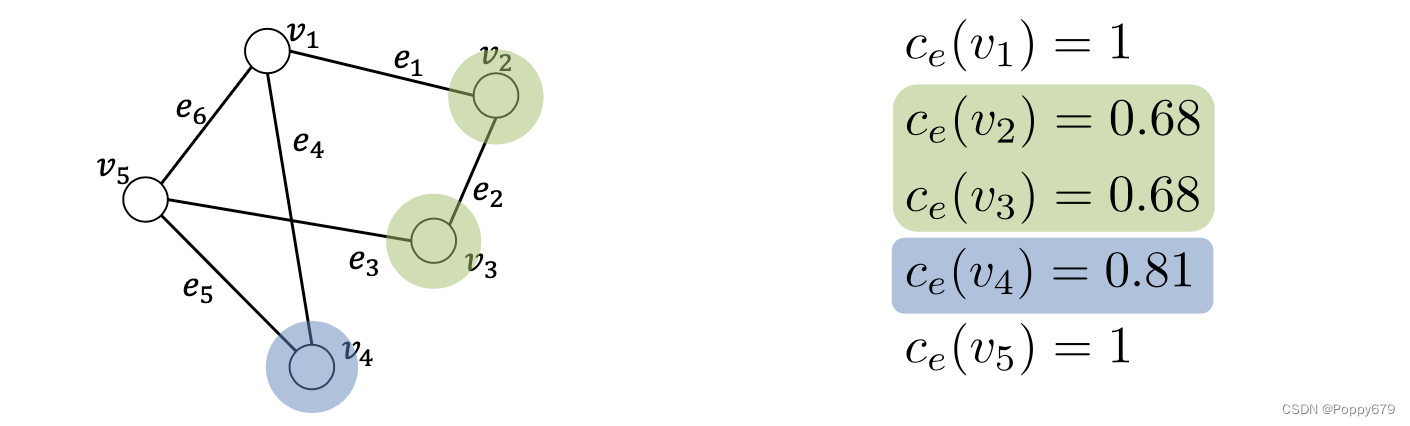
特征向量中心性
衡量节点的中心性同时考虑邻居节点的中心性
c
e
(
v
i
)
=
1
λ
∑
j
=
1
N
A
i
,
j
?
c
e
(
v
j
)
c_{e}\left(v_{i}\right)=\frac{1}{\lambda} \sum_{j=1}^{N} \mathbf{A}_{i, j} \cdot c_{e}\left(v_{j}\right)
ce?(vi?)=λ1?∑j=1N?Ai,j??ce?(vj?) -->
λ
?
c
e
=
A
?
c
e
\lambda \cdot \mathbf{c}_{e}=\mathbf{A} \cdot \mathbf{c}_{e}
λ?ce?=A?ce?
Katz中心性
Katz是特征向量中心性的一个变种,beta其实是针对节点i自身的一个重要性
c
k
(
v
i
)
=
α
∑
j
=
1
N
A
i
,
j
c
k
(
v
j
)
+
β
c_{k}\left(v_{i}\right)=\alpha \sum_{j=1}^{N} \mathbf{A}_{i, j} c_{k}\left(v_{j}\right)+\beta
ck?(vi?)=α∑j=1N?Ai,j?ck?(vj?)+β
c k = ( I ? α ? A ) ? 1 β \mathbf{c}_{k}=(\mathbf{I}-\alpha \cdot \mathbf{A})^{-1} \boldsymbol{\beta} ck?=(I?α?A)?1β
0
<
α
<
1
λ
0 < \alpha < \frac{1}{\lambda}
0<α<λ1?