背景
本文介绍ICML2021 I-BERT:?Integer-only BERT Quantization
文章目的是对BERT进行更彻底的量化和整型计算;
作者认为之前的量化方案没有对gelu、softmax这些非线性操作进行量化计算(如下图1),即保持了float类型的计算,不仅影响计算效率,而且不能部署到某些只支持整型计算的芯片上;
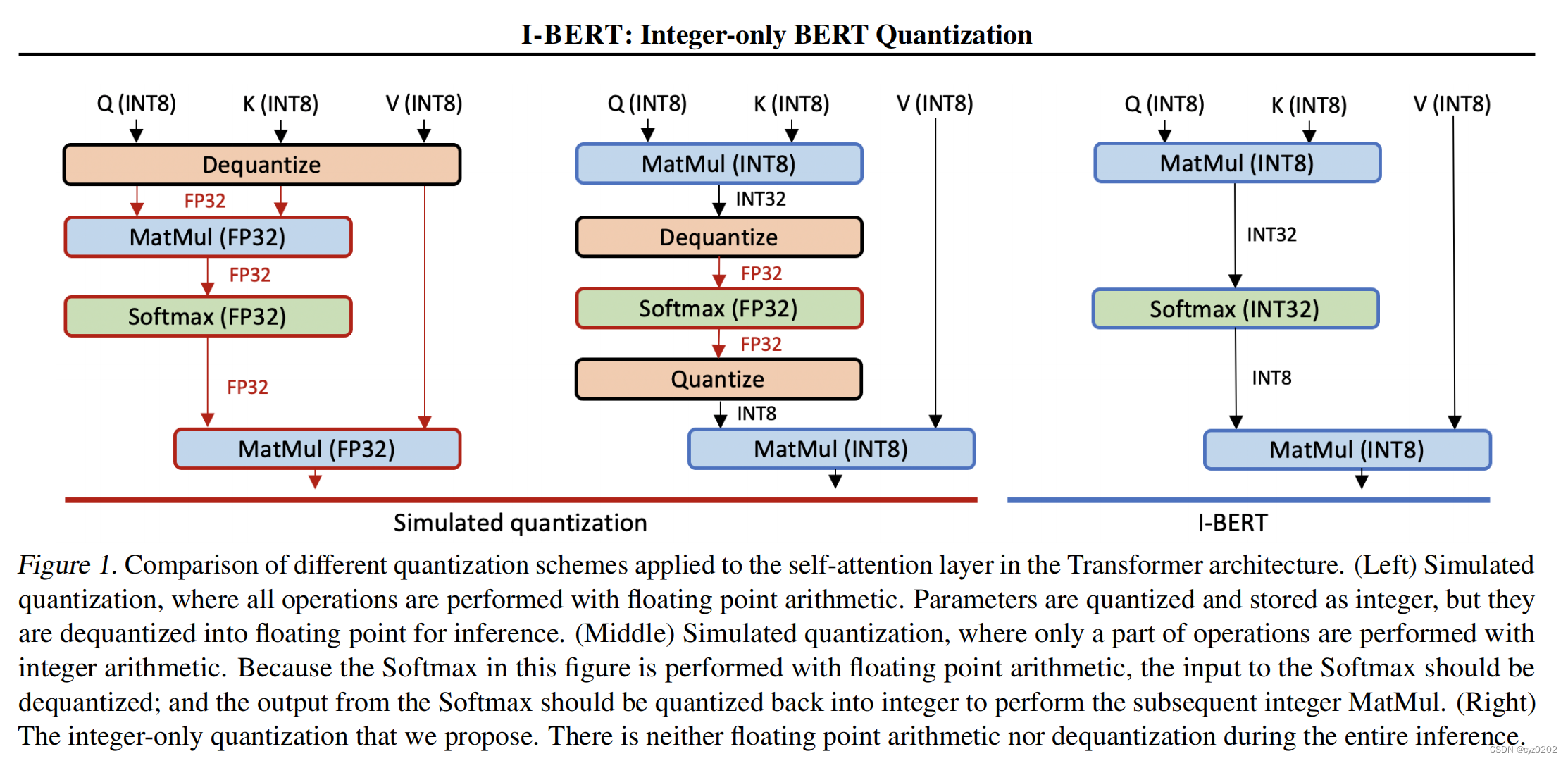
???
作者采用的量化方案是 8bits 对称量化;
已有方案和不足
作者主要解决GELU、softmax这两类非线性层的量化问题;
先来看看GELU的表达式,如下,erf被称为error function
其中??
且??
GELU本身难以直接实现量化,强行量化会导致较大精度损失;
不像线性层(如矩阵乘积、分段线性的RELU等),利用线性性质可以较好地反量化到float计算结果( 作者举例?MatMul(Sq) = S*MatMul(q),其中x=Sq,S为scale,q为x的量化值 );
已有的一些近似GELU的方案,包括:
- sigmoid近似,如下,引入非线性sigmoid,仍然不好整型计算
- ReLU6近似,如下,使用ReLU6,虽然可以整型化,但是效果不佳;该方案也被称为h-GELU
下图2左图展示了h-GELU的缺点
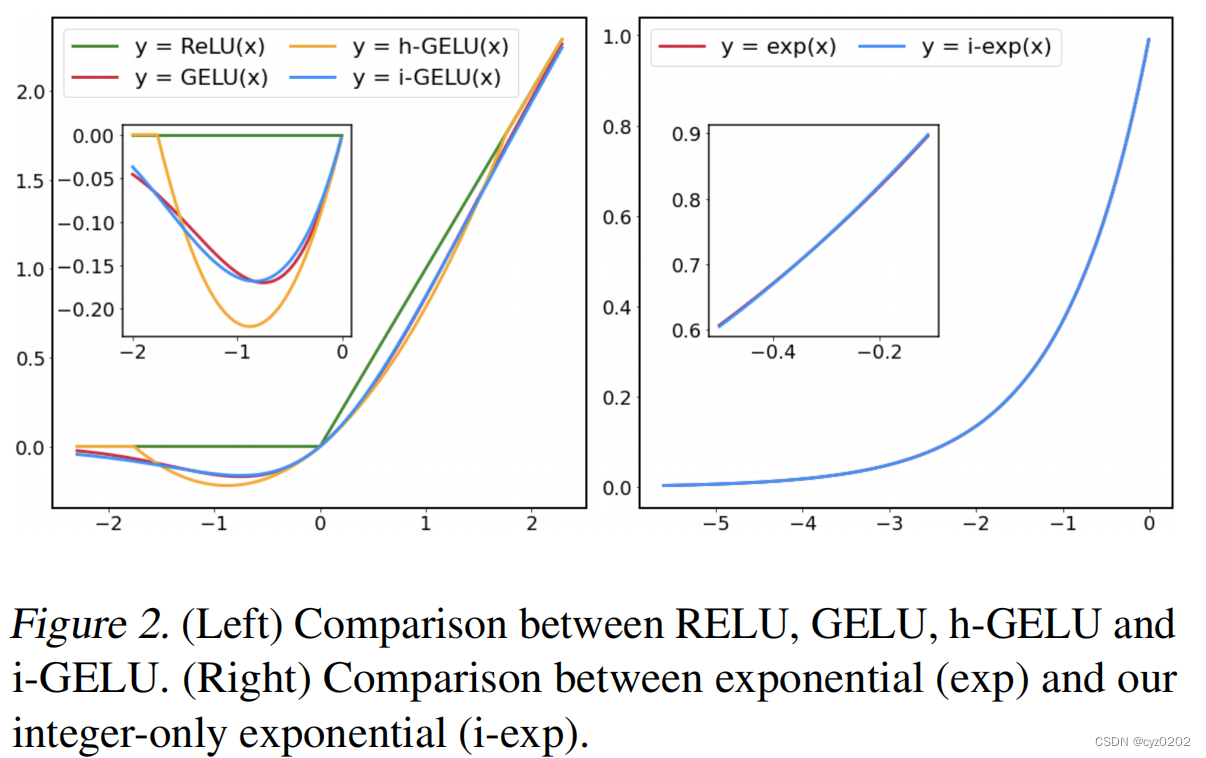
GELU的解决方案
作者通过分析,认为可以引入二阶多项式对erf进行近似,进一步对GELU进行近似,计算方式如下
这个想法来自于任意函数可由多项式函数拟合的理论,将该类型多项式称为interpolating polynomials(插值多项式);详情请移步原文;
直接优化上式得到的结果并不理想,原因是erf的定义域是实域范围;
考虑到erf的值域在[-1, 1],且erf是个奇函数,即
因此作者通过设计正实数域部分,并推广到负实数域,得到如下L(x),
,其中
clip中的max表示|x|最大取值为-b;
因此,且为奇函数;
a、b是通过找一些GELU上的点来进行拟合求解的;
如上可得,
i-GELU的量化方案
有了GELU的多项式表达形式,就可以开始设计量化方案了;
L(x)是个多项式,因此得先知道怎么对多项式量化;
作者给出了多项式量化算法 I-POLY,如下

?
可以验证?,
因此任意2阶多项式的量化、反量化都可以采用上述算法;
(注:个人感觉这里的量化属于一种为了计算量化而量化;计算过程没问题,就是感觉是故意构造出来的那种,q_out和S_out都未必是多项式结果的真实量化值和scale)
------
有了多项式量化方法,就可以继续实现I-GELU的量化方案了,计算过程如下

调用栈为 I-GELU -> I-ERF -> I-POLY
注意图4算法中的一些实现小技巧,如
?,
??
注意到上式 max=-b/S,可能得改成 max=round(-b/S),不然q’没法保证是整型。。。
------
以上即为I-GELU的实现过程,效果如下
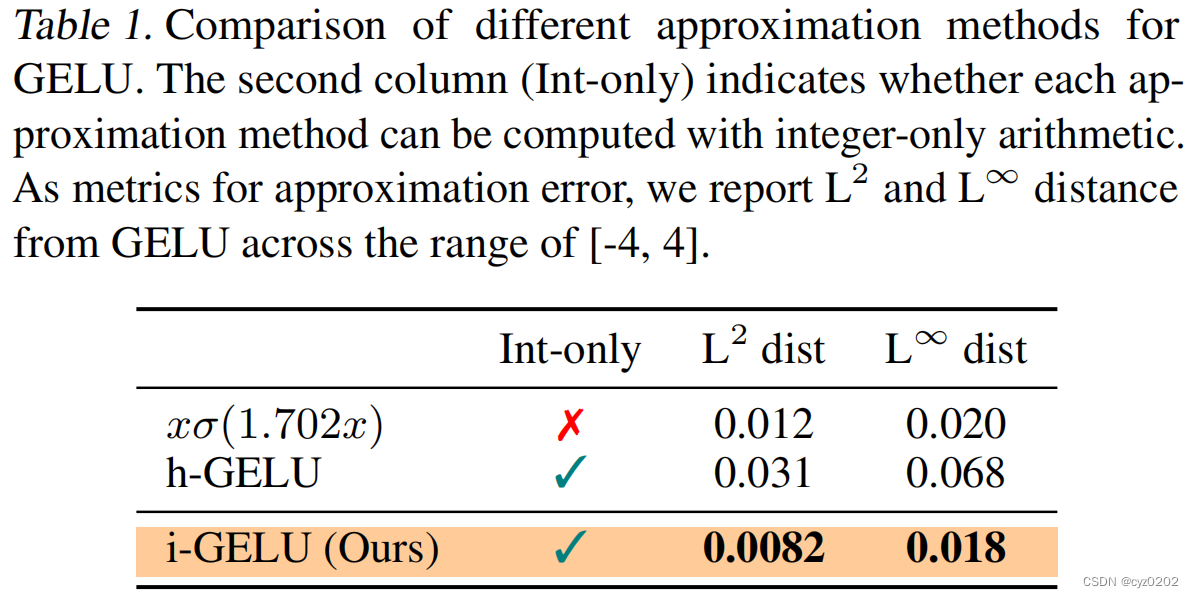
????
SOFTMAX的解决方案
- 利用高阶多项式进行近似,可用场景很有限;
SOFTMAX的量化方案
为了数值稳定性,作者首先对softmax进行处理,如下
值得一提的是,
对于一个非正实数,可以通过下式对其进行近似
其中z(商)是一个非负整数,p(余数)取值范围?;
则有
上式 >> 表示右移操作;
进一步,如果能将表示为整型计算,那么就能对所有
以及Softmax进行整型计算了;
而且?中 p的取值范围 相对x或者
?缩小了很多,可以更好地做近似;
回想GELU,作者提出通过 2阶多项式近似非线性函数;这里也可以这样做;
作者寻找的近似二阶多项式的方法,是通过在
范围内计算下式最优解:
?
最终得到
则
其中?,
图2右图展示了上述近似有着很好的效果;
多项式的量化计算方法 I-POLY 在上面已经介绍过了,所以整个Softmax的量化计算方法为

?基本思想和I-GELU差不多
#TODO#:最后一步??好像有点问题。。。
LayerNorm的量化方案?
?- 待续
I-BERT的实现解析
- 将放在另一篇文章中讨论
总结
- 本文介绍了I-BERT的改进点及 GELU/SOFTMAX 的整型化计算 实现方法;
- 主要思想是通过2阶多项式进行近似,再对2阶多项式进行量化计算;