防御对抗攻击:Gotta Catch ’Em All: Using Honeypots to Catch Adversarial Attacks on Neural Networks (CCS '20: Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications SecurityOctober 2020)
论文背景
??深度神经网络 (DNN) 容易受到对抗性攻击(主要的攻击方法:FGSM,PGD,CW,Elastic Net,BPDA,SPSA 暂时没有深入调研攻击方式,后面会陆续给出几种攻击方式的原理),只要提供经过训练的模型,就可以修改输入从而产生错误输出。这些修改后的对抗样本能有效欺骗在不同训练数据不同子集上的训练模型。事实证明,对抗性攻击对部署在现实环境中的模型有效,例如无人驾驶汽车、面部识别和物体识别系统。针对对抗性攻击已有的防御方法主要有两种 “对抗训练(Adversarial training)” 和 “梯度掩蔽(Gradient masking)” 。
??对抗训练:在对抗性训练中,防御者通过将对抗性示例合并到训练数据集中来为模型接种疫苗以抵御给定的攻击。 这种 “对抗性” 训练过程降低了模型对特定已知攻击的敏感性。
??梯度掩蔽:防御者训练一个具有小梯度的模型,使得模型对输入空间上小的变化具有鲁棒性(例如对抗性干扰),“防御性蒸馏” 就是该方法的一个例子,首先正常训练得到模型一
F
θ
\mathcal{F}_\theta
Fθ?,然后使用
F
θ
\mathcal{F}_\theta
Fθ?输出的分类概率作为输入训练得到模型二
F
θ
′
\mathcal{F}^\prime_\theta
Fθ′?, 用
F
θ
′
\mathcal{F}^\prime_\theta
Fθ′?替代
F
θ
\mathcal{F}_\theta
Fθ?达到梯度掩蔽的目的。
??但是 (1) “对抗训练” 可以使用新的攻击或对已知攻击的不同参数来攻破。(2) “梯度掩蔽" 可以从对抗样本的生成上小的调整可以克服这种防御。
整体框架
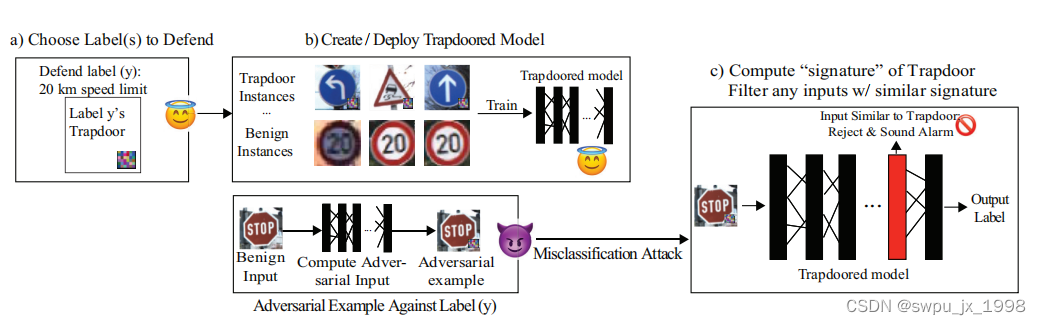
作者提出了一种新的 “陷门防御(trapdoor defense)”
a) 选择需要防御的目标标签。b) 为每个目标标签创建不同的陷门并将它们嵌入到模型中。 为每个嵌入式陷门部署模型并计算激活签名。 c) 可以访问模型的对手构建了一个对抗样本。 在运行时,模型将每个输入的神经元激活特征与陷门的特征进行比较。 因此,它识别出攻击并发出警报。
理论依据
??理论上来说,trapdoor 是为特定的标签
y
t
y_t
yt? 设计的特有的扰动,用
Δ
\Delta
Δ 表示,这样模型会把任何包含
Δ
\Delta
Δ 的输入
x
x
x 都分类为
y
t
y_t
yt?, 也就是说
F
θ
(
x
+
Δ
)
=
y
t
,
?
x
\mathcal{F}_{\theta}(x + \Delta) = y_t, \forall x
Fθ?(x+Δ)=yt?,?x。对于攻击者来说,如果其目标是
y
t
y_t
yt?, 那么就需要找到一个扰动
?
\epsilon
? 使得
F
θ
(
x
+
?
)
=
y
t
=?
F
θ
(
x
)
\mathcal{F}_{\theta}(x + \epsilon) = y_t\not=\mathcal{F}_{\theta}(x)
Fθ?(x+?)=yt??=Fθ?(x), 进一步说,就是使得优化函数的损失最小,即
m
i
n
J
(
y
t
,
F
θ
(
x
+
?
)
)
\rm{min} \it{J(y_t,\mathcal{F}_\theta(x+\epsilon))}
minJ(yt?,Fθ?(x+?))。如果一个模型已经注入了
Δ
\Delta
Δ , 那么攻击者的优化函数会收敛到靠近 trapdoor 的损失函数的邻域内。下图是一个正常模型和trapdoored模型的损失函数的假设图,trapdoor 在A和B之间创造了一个大的局部最小值,攻击者的损失函数会收敛到这个局部最小值(这一部分的理论证明会在后面给出,下面先来看看具体的做法)
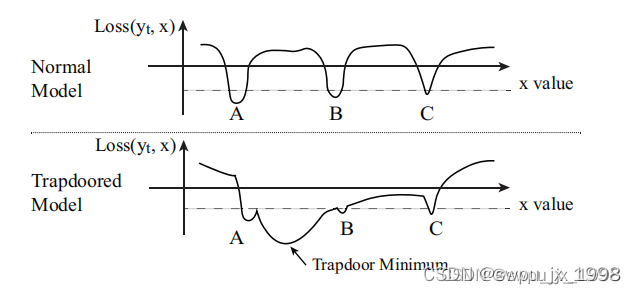
单标签防御
Step 1: Embedding Trapdoors
??首先通过将陷门扰动注入随机选择的正常输入并将它们与标签
y
t
y_t
yt? 关联而生成的新实例来扩充原始训练数据集,从而创建陷门训练数据集。新实例定义如下
x
′
=
x
+
Δ
:
=
I
(
x
,
M
,
δ
,
k
)
,
x^\prime = x + \Delta := \mathcal{I}(x, \it{M}, \it{\delta}, k),
x′=x+Δ:=I(x,M,δ,k),
其中
x
i
,
j
,
c
′
=
(
1
?
m
i
,
j
,
c
)
?
x
i
,
j
,
c
+
m
i
,
j
,
c
?
δ
i
,
j
,
c
x^{\prime}_{i,j,c} = (1-m_{i,j,c}) \cdot x_{i,j,c} + m_{i,j,c}\cdot \delta_{i,j,c}
xi,j,c′?=(1?mi,j,c?)?xi,j,c?+mi,j,c??δi,j,c?, 这里
I
(
?
)
\mathcal{I}(\cdot)
I(?) 是注入函数,
Δ
=
(
M
,
δ
,
k
)
\Delta = (M,\delta,k)
Δ=(M,δ,k) 是
y
t
y_t
yt? 的扰动。
δ
,
M
\delta, M
δ,M 和
x
x
x 具有相同的形状,
δ
\delta
δ 是扰动模式,是一个随机值矩阵。
M
M
M 是
t
r
a
p
d
o
o
r
??
m
a
s
k
trapdoor \; mask
trapdoormask,指定了扰动应该覆盖原始图像的程度,
M
M
M中的每一个元素
m
i
,
j
,
c
∈
[
0
,
1
]
m_{i,j,c} \in [0,1]
mi,j,c?∈[0,1] 。文中设置
m
i
,
j
,
c
∈
{
0
,
k
}
m_{i,j,c} \in \{0, k\}
mi,j,c?∈{0,k},
k
<
<
1
k << 1
k<<1。
k
k
k 称为
m
a
s
k
??
r
a
t
i
o
mask \; ratio
maskratio (覆盖比例) 。
如何为每个标签制作不同的 trapdoor?
??不同标签的 trapdoor 需要不同的内部神经元表示。这种区别允许每个不同的神经元作为签名来检测针对其各自受保护标签的对抗性示例。为了确保可区分性,我们将每个 trapdoor 构建为随机选择的一组 5 个正方形(每个 3 x 3 像素)散布在图像上。为了进一步区分 trapdoor,每个 3 x 3 正方形的强度从
N
(
μ
,
σ
)
\mathcal{N}(\mu,\sigma)
N(μ,σ) 中独立采样,其中
μ
∈
[
0
,
255
]
\mu \in [0,255]
μ∈[0,255] 和
σ
∈
[
0
,
255
]
\sigma \in [0,255]
σ∈[0,255] 分别为每个 trapdoor 选择。 活板门的示例图像如下。

Step 2: Training the Trapdoored Model
??trapdoor model的目标是对于干净的图片能达到很高的准确率,同时把任何包含
Δ
=
(
M
,
δ
,
k
)
\Delta=(M,\delta,k)
Δ=(M,δ,k) 的图片分类为
y
t
y_t
yt?。这一优化目标和向神经网络注入一个后门的过程很相似。
m
i
n
θ
??
J
(
y
,
F
θ
(
x
)
)
+
λ
?
J
(
y
t
,
F
θ
(
x
+
Δ
)
)
?
x
∈
X
??
w
h
e
r
e
??
y
=?
y
t
,
\underset{\theta}{\rm{min}}\; J(y,\mathcal{F}_{\theta}(x)) + \lambda\cdot J(y_t, \mathcal{F}_{\theta}(x+\Delta)) \\ \forall x \in \mathcal{X} \; \rm{where} \; \it{y} \not= y_t,
θmin?J(y,Fθ?(x))+λ?J(yt?,Fθ?(x+Δ))?x∈Xwherey?=yt?,
其中
y
y
y 是
x
x
x 的真实标签。训练好一个trapdoor model 后,定义
Δ
\Delta
Δ 的
“
t
r
a
p
d
o
o
r
??
s
i
g
n
a
t
u
r
e
”
“trapdoor\; signature”
“trapdoorsignature” 表示如下
S
Δ
=
E
x
∈
X
,
y
t
=?
F
θ
(
x
)
g
(
x
+
Δ
)
,
\mathcal{S}_{\Delta} = \mathbf{E}_{x\in \mathcal{X},y_t \not=\mathcal{F}_{\theta}(x)}g(x + \Delta),
SΔ?=Ex∈X,yt??=Fθ?(x)?g(x+Δ),
其中
E
(
?
)
\mathbf{E}(\cdot)
E(?) 表示期望,
g
(
?
)
g(\cdot)
g(?) 是模型对输入
x
x
x 的特征表示,文中作者应用的是模型的最后一层 softmax 层的输入。
S
Δ
\mathcal{S}_{\Delta}
SΔ? 的定义分析在后面会给出。下图简单的描述了
S
Δ
\mathcal{S}_{\Delta}
SΔ? 的计算过程。
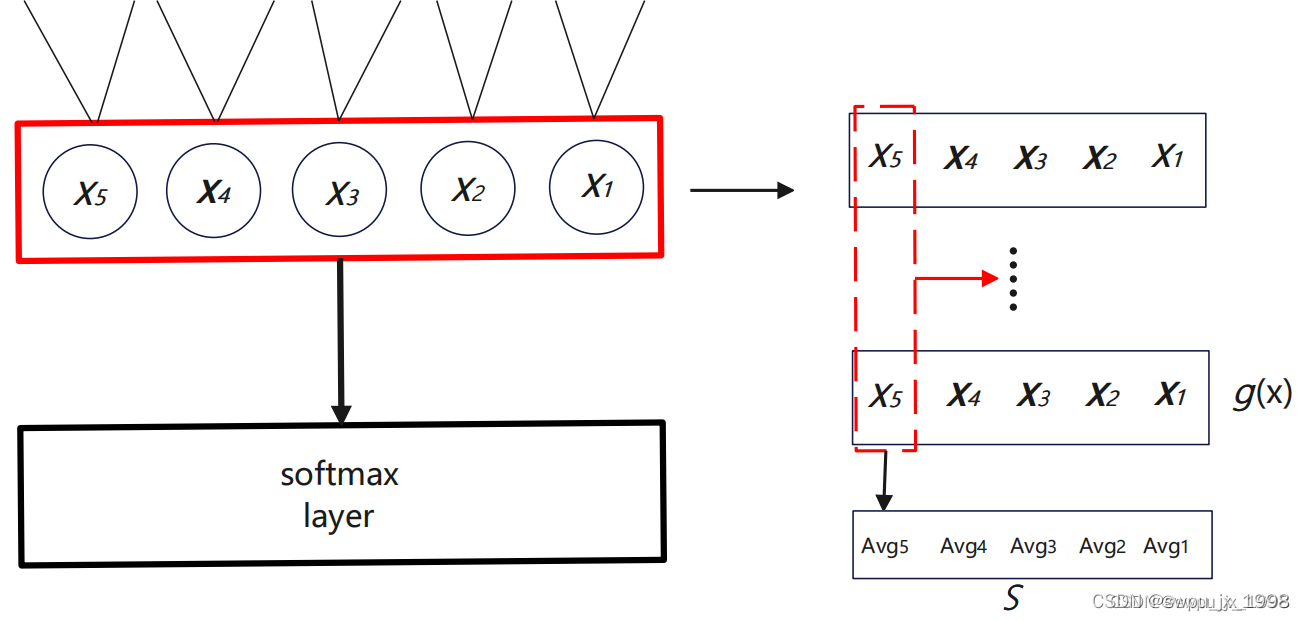
Step 3: Detecting Adversarial Attacks
??对于目标 y t y_t yt? 的对抗样本 x + ? x+\epsilon x+? 输入到训练好的trapdoor model,可以得到 g ( x + ? ) g(x + \epsilon) g(x+?),通过比较 g ( x + ? ) g(x + \epsilon) g(x+?) 和 S Δ \mathcal{S}_{\Delta} SΔ? 的相似程度来检测对抗样本。文中使用 cosine 相似度来衡量二者之间的相似性,即 c o s ( g ( x + ? ) , S Δ ) cos(g(x+\epsilon),\mathcal{S}_{\Delta}) cos(g(x+?),SΔ?)。如果相似度超过一个预设的阈值 ? t \phi_t ?t?,那么就认为是对抗样本。文中通过计算已知良性图像和陷门图像之间相似度的统计分布来配置 ? t \phi_t ?t?。
多标签防御
??通过单个标签的防御可以扩展到多标签的防御。另
Δ
t
=
(
M
t
,
δ
t
,
k
t
)
\Delta_t = (M_t,\delta_t,k_t)
Δt?=(Mt?,δt?,kt?) 代表标签
y
t
y_t
yt?。相应的用于训练保护所有标签的陷阱模型的优化函数定义为
m
i
n
θ
??
J
(
y
,
F
θ
(
x
)
)
+
λ
?
∑
y
t
∈
Y
,
y
t
=?
y
J
(
y
t
,
F
θ
(
x
+
Δ
t
)
)
\underset{\theta}{\rm{min}}\; J(y,\mathcal{F}_{\theta}(x)) + \lambda\cdot \sum_{ y_t\in \mathcal{Y}, y_t\not=y}J(y_t,\mathcal{F}_{\theta}(x + \Delta_t))
θmin?J(y,Fθ?(x))+λ?yt?∈Y,yt??=y∑?J(yt?,Fθ?(x+Δt?))
Evading Adversarial Example Detection Defenses with Orthogonal Projected Gradient Descent
符号系统定义
分类模型
f
:
R
d
→
R
n
f:\mathbb{R}^d \to \mathbb{R}^n
f:Rd→Rn ,输入
x
∈
R
d
x\in \mathbb{R}^d
x∈Rd,输出
f
(
x
)
∈
R
n
f(x)\in \mathbb{R}^n
f(x)∈Rn.
检测约束:
g
:
R
d
→
R
g:\mathbb{R}^d \to \mathbb{R}
g:Rd→R,
g
(
x
)
<
0
g(x) < 0
g(x)<0 满足条件,
g
(
x
)
>
0
g(x) > 0
g(x)>0 不满足条件.
真实标签:
c
(
x
)
=
y
c(x)=y
c(x)=y.
损失函数:
L
\mathcal{L}
L.
嵌入向量:
e
(
x
)
e(x)
e(x) 表示输入
x
x
x 在
f
f
f 的中间层上的嵌入。除非另有指定,否则
e
e
e返回紧邻 softmax 激活之前的 logit 向量.
使用投影梯度法生成对抗样本
??梯度投影法的基本思想:当迭代点
x
k
x_k
xk? 是可行域
D
\mathcal{D}
D 的内点时,取
d
=
?
?
f
(
x
k
)
d= -\nabla f(x_k)
d=??f(xk?) 作为搜索方向;否则,当
x
k
x_k
xk? 是可行域
D
\mathcal{D}
D 的边界点时,取
?
?
f
(
x
k
)
-\nabla f(x_k)
??f(xk?) 这些边界面交集上的投影作为搜索方向。
??给定损失函数
L
(
f
,
x
,
t
)
\mathcal{L}(f,x,t)
L(f,x,t),输入参数分别是分类模型,训练样本,目标标签。给定约束条件
S
?
=
{
z
:
d
(
x
,
z
)
<
?
}
S_\epsilon = \{z:d(x,z)<\epsilon\}
S??={z:d(x,z)<?},优化目标定义为
x
′
=
arg?min
?
z
∈
S
?
L
(
f
,
z
,
t
)
x^\prime = \argmin_{z\in S_\epsilon} \mathcal{L}(f,z,t)
x′=z∈S??argmin?L(f,z,t)
迭代步骤定义为
x
i
+
1
=
P
S
?
(
x
i
?
α
?
x
i
L
(
f
,
z
,
t
)
)
x_{i+1} = P_{S_\epsilon}(x_i - \alpha\nabla_{x_i}\mathcal{L}(f,z,t))
xi+1?=PS???(xi??α?xi??L(f,z,t))
其中
P
S
?
(
z
)
P_{S_\epsilon}(z)
PS???(z) 表示
z
z
z 在
S
?
S_\epsilon
S?? 上的投影。例如,投影
P
S
?
(
z
)
P_{S_\epsilon}(z)
PS???(z) 在约束
d
(
x
,
z
)
=
∥
x
?
z
∥
∞
d(x,z)=\|x-z\|_\infin
d(x,z)=∥x?z∥∞? 下是通过把
z
z
z 裁剪到
[
x
?
?
,
x
+
?
]
[x-\epsilon, x+\epsilon]
[x??,x+?]。
选择性梯度下降
??现有的用于对抗神经网络的检测策略的方法定义如下
arg?min
?
x
∈
S
?
L
(
f
,
x
,
t
)
+
λ
g
(
x
)
\argmin_{x\in S_\epsilon} \mathcal{L}(f,x,t) + \lambda g(x)
x∈S??argmin?L(f,x,t)+λg(x)
其中,
λ
\lambda
λ 是一个超参数,它控制着欺骗分类器和欺骗检测器的相对重要性。
??不同于上面的方式,文中没有最小化
f
f
f 和
g
g
g 的加权和,而是采用分步优化的方式,其攻击方法定义如下
A
(
x
,
t
)
=
arg?min
?
x
′
:
∥
x
?
x
′
∥
<
?
L
(
f
,
x
′
,
t
)
?
I
(
f
(
x
)
=?
t
)
+
g
(
x
′
)
?
I
(
f
(
x
)
=
t
)
?
L
u
p
d
a
t
e
(
x
,
t
)
\mathcal{A}(x,t) = \argmin_{x^\prime:\|x-x^\prime\| < \epsilon} \underbrace{\mathcal{L}(f,x^\prime,t)\cdot \mathbb{I}(\it{f(x)\not=t)} + g(x^\prime) \cdot \mathbb{I}(\it{f(x)=t})}_{\mathcal{L}_{\rm{update}}(x,t)}
A(x,t)=x′:∥x?x′∥<?argmin?Lupdate?(x,t)
L(f,x′,t)?I(f(x)?=t)+g(x′)?I(f(x)=t)??
??这里的想法是,我们不是最小化两个损失函数的凸组合,而是根据
f
(
x
)
=
t
f(x)=t
f(x)=t 是否成立选择性地优化
f
f
f 或
g
g
g,确保更新总是有助于改善
f
f
f 的损失或
g
g
g 的损失。
??这种优化方式的另一个好处是,它将梯度下降步骤分解为两个更新,这防止了梯度不平衡问题:其中两个损失函数的梯度大小不相同,将导致优化过程不稳定。上面的公式可以简化为如下的形式
?
L
u
p
d
a
t
e
(
x
,
t
)
=
{
?
L
(
f
,
x
,
t
)
if?
f
(
x
)
=?
t
,
?
g
(
x
)
if?
f
(
x
)
=
t
.
\nabla\mathcal{L}_{\rm{update}}(x,t) = \begin{cases} \nabla \mathcal{L}(f,x,t) & \text {if $f(x) \not= t$,} \\ \nabla g(x) & \text{if $f(x)=t$.} \end{cases}
?Lupdate?(x,t)={?L(f,x,t)?g(x)?if?f(x)?=t,if?f(x)=t.?
正交梯度下降
上面的攻击方法在数学上是正确的,但是可能会遇到数值不稳定的困难。通常,
f
f
f 和
g
g
g 的梯度指向相反的方向,因此,花费在优化
f
f
f 上的每一步都会导致对
g
g
g 进行优化的倒退。这将导致优化器在执行的每一步之后都不断地“撤消”它自己的进度。我们通过给出一个稍微不同的更新规则来解决这个问题,更新上面的公式如下
?
L
u
p
d
a
t
e
(
x
,
t
)
=
{
?
L
(
f
,
x
,
t
)
?
p
r
o
j
?
L
(
f
,
x
,
t
)
?
g
(
x
)
if?
f
(
x
)
=?
t
,
?
g
(
x
)
?
p
r
o
j
?
g
(
x
)
?
L
(
f
,
x
,
t
)
if?
f
(
x
)
=
t
.
\nabla\mathcal{L}_{\rm{update}}(x,t) = \begin{cases} \nabla \mathcal{L}(f,x,t) - \rm{proj}_{\it{\nabla \mathcal{L}(f,x,t)}} \it{\nabla g(x)} & \text {if $f(x) \not= t$,} \\ \nabla g(x)-\rm{proj}_{\it{\nabla g(x)}}\it{\nabla \mathcal{L}(f,x,t)} & \text{if $f(x)=t$.} \end{cases}
?Lupdate?(x,t)={?L(f,x,t)?proj?L(f,x,t)??g(x)?g(x)?proj?g(x)??L(f,x,t)?if?f(x)?=t,if?f(x)=t.?
其中
p
r
o
j
?
L
(
f
,
x
,
t
)
?
g
(
x
)
\rm{proj}_{\it{\nabla \mathcal{L}(f,x,t)}} \it{\nabla g(x)}
proj?L(f,x,t)??g(x) 表示梯度
?
L
(
f
,
x
,
t
)
\nabla \mathcal{L}(f,x,t)
?L(f,x,t) 在
?
g
(
x
)
\nabla g(x)
?g(x) 上的投影,
p
r
o
j
?
g
(
x
)
?
L
(
f
,
x
,
t
)
\rm{proj}_{\it{\nabla g(x)}}\it{\nabla \mathcal{L}(f,x,t)}
proj?g(x)??L(f,x,t) 同理。这里使用到了数学上的施密特正交化,下面简单解释以下:
??假设有两个线性无关的向量
a
→
\overrightarrow{a}
a 和
b
→
\overrightarrow{b}
b, 现在要将两个向量正交化。首先是保持
a
→
\overrightarrow{a}
a 不动,让
a
→
=
A
\overrightarrow{a} = A
a=A, 接下来寻找另一个向量
B
B
B, 使得
A
⊥
B
A \bot B
A⊥B。如下图,
p
→
\overrightarrow{p}
p? 是
b
→
\overrightarrow{b}
b 在
a
→
\overrightarrow{a}
a 上的投影,
B
B
B 就相当于
b
→
\overrightarrow{b}
b 的误差向量:
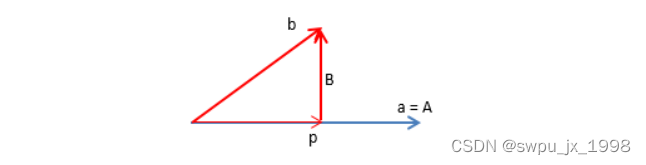
通过公式计算
x
x
x,
x
x
x 是一个标量
x
=
a
→
?
b
→
a
→
?
a
→
x = \frac{\overrightarrow{a}^\top \overrightarrow{b}}{\overrightarrow{a}^\top \overrightarrow{a}}
x=a?aa?b?
p
→
=
a
→
x
=
x
a
→
=
a
?
b
a
?
a
a
→
\overrightarrow{p} = \overrightarrow{a}x=x\overrightarrow{a}=\frac{a^\top b}{a^\top a}\overrightarrow{a}
p?=ax=xa=a?aa?b?a
B
=
b
→
?
p
→
B = \overrightarrow{b}-\overrightarrow{p}
B=b?p?
结合公式中
p
r
o
j
?
L
(
f
,
x
,
t
)
?
g
(
x
)
\rm{proj}_{\it{\nabla \mathcal{L}(f,x,t)}} \it{\nabla g(x)}
proj?L(f,x,t)??g(x) 就表示
p
p
p,
?
L
(
f
,
x
,
t
)
?
p
r
o
j
?
L
(
f
,
x
,
t
)
?
g
(
x
)
\nabla \mathcal{L}(f,x,t) - \rm{proj}_{\it{\nabla \mathcal{L}(f,x,t)}} \it{\nabla g(x)}
?L(f,x,t)?proj?L(f,x,t)??g(x) 就表示
B
B
B
Feature-Indistinguishable Attack to Circumvent Trapdoor-Enabled Defense
基本思路
??文中提出了一种新的黑盒对抗性攻击方法,称为特征不可区分攻击(FIA)。它通过制作在特征(即神经元激活)空间中与目标类别中的良性样本难以区分的对抗性样本来绕过 TeD。为了实现这一目标,FIA 通过最小化对抗样本与目标类别中良性样本特征表示期望的距离,并最大化对抗样本与准备阶段被TeD检测出来的对抗样本的距离。利用一个约束条件,确保生成的对抗性样本的特征向量在目标类别中良性样本的特征向量的分布范围内。
Basic Scheme
??为了避免陷阱检测,我们的目标是使特征空间中对抗性的样本与良性目标的样本难以区分。一旦一个对抗样本在适当的 latent层与良性目标样本无法区分,陷阱防御不太可能被检测到,除非陷阱防御是不切实际的,对良性目标样本的高假阳性率。为了实现这一目标,我们需要一个损失函数,它可以将对抗样本引入特征空间中良性目标样本的分布。
Optimization Problem: 目标类别的集合
C
t
C_t
Ct?,输入样本
x
∈
X
x \in \mathcal{X}
x∈X,并且
x
?
C
t
x \notin C_t
x∈/?Ct?,
D
t
\mathcal{D}_t
Dt? 是
C
t
C_t
Ct? 在模型的
L
L
L 层的输出特征的分布,叫做
g
e
n
e
r
a
t
i
o
n
generation
generation
l
a
y
e
r
layer
layer,
F
L
(
x
)
\mathcal{F}_L(x)
FL?(x) 表示模型在选择的
L
L
L 层的输出,FIA 的基本策略是最小化对抗样本的潜在特征
F
L
(
x
+
?
)
\mathcal{F}_L(x + \epsilon)
FL?(x+?) 和目标样本的
F
L
t
g
t
∈
D
t
\mathcal{F}_L^{tgt} \in \mathcal{D}_t
FLtgt?∈Dt? 的距离,定义如下:
min
?
?
D
(
F
L
(
x
+
?
)
,
F
L
t
g
t
)
,
s
.
t
.
F
L
(
x
+
?
)
∈
D
t
\min_\epsilon \mathbf{D}(\mathcal{F}_L(x+\epsilon), \mathcal{F}_L^{tgt}),\\ \rm{s.t.} \mathcal{F}_L(x + \epsilon) \in \mathcal{D}_t
?min?D(FL?(x+?),FLtgt?),s.t.FL?(x+?)∈Dt?
其中
D
\mathbf{D}
D 是距离函数。上面式子的约束条件确保生成的对抗样本和良性的目标样本是不可区分。
??FIA在公式中使用了两个距离损失函数,并且同时最小化这两个距离。一个是
L
2
L_2
L2? 的距离。它的目标是将对抗样本引入目标类别
C
t
C_t
Ct?。另一个是与目标的余弦相似度。它的目标是确保一个对抗样本有一个类似于目标表示方向的特征向量,依赖于特征空间中与活板门签名的余弦相似性来检测的陷门防御模型,不太可能检测到它。最优化问题将变成:
min
?
?
{
?
c
o
s
(
F
L
(
x
+
?
)
,
F
L
t
g
t
)
+
λ
?
∥
F
L
(
x
+
?
)
?
F
L
t
g
t
∥
2
}
,
s
.
t
.
F
L
(
x
+
?
)
∈
D
t
\min_\epsilon\{-cos(\mathcal{F}_L(x+\epsilon),\mathcal{F}_L^{tgt})+\lambda \cdot \| \mathcal{F}_L(x+\epsilon)-\mathcal{F}_L^{tgt} \|_2\},\\ \rm{s.t.} \mathcal{F}_L(x+\epsilon) \in \mathcal{D}_t
?min?{?cos(FL?(x+?),FLtgt?)+λ?∥FL?(x+?)?FLtgt?∥2?},s.t.FL?(x+?)∈Dt?
Basic Scheme: 为了确保方程式中的约束条件。我们需要估计目标类别
C
t
C_t
Ct? 的特征表示分布
D
t
\mathcal{D}_t
Dt?。 FIA 采用了一种不太准确但简单的方法:我们假设目标类别
𝐶
𝑡
𝐶_𝑡
Ct? 中良性示例的特征表示可以形成一个凸区域. 有了这个假设,我们可以选择良性示例的特征表示的期望作为目标表示
F
L
t
g
t
=
F
L
C
t
=
E
x
∈
C
t
F
L
(
x
)
\mathcal{F}_L^{tgt} = \mathcal{F}_L^{C_t} = \mathbf{E}_{x\in C_t}\mathcal{F}_L(x)
FLtgt?=FLCt??=Ex∈Ct??FL?(x)
其中
E
(
?
)
\mathbf{E}(\cdot)
E(?) 是期望函数,使用良性样本
F
L
(
x
)
\mathcal{F}_L(x)
FL?(x) 与
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt?? 的余弦相似度分布作为
D
t
\mathcal{D}_t
Dt? 的近视分布。
??由于期望对离群值很敏感,所以我们在计算等式中的期望之前,使用 DBSCAN 来确定并去除离群值 : 位于特征空间中最低密度区域的良性目标样本的一定比例(在我们的评估中为10%)被视为异常值并去除。然后,我们计算一个阈值
c
p
c_p
cp?,即期望和良性目标样本之间的最小余弦相似度。我们要求一个对抗样本的代表特征与期望
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt?? 的余弦相似度在
c
p
c_p
cp? 范围内。
min
?
?
{
?
c
o
s
(
F
L
(
x
+
?
)
,
F
L
C
t
)
+
λ
?
∥
F
L
(
x
+
?
)
?
F
L
C
t
∥
2
}
,
s
.
t
.
c
o
s
(
F
L
(
x
+
?
)
,
F
L
C
t
)
≥
c
p
\min_\epsilon\{-cos(\mathcal{F}_L(x+\epsilon),\mathcal{F}_L^{C_t})+\lambda \cdot \| \mathcal{F}_L(x+\epsilon)-\mathcal{F}_L^{C_t} \|_2\},\\ \rm{s.t.} cos(\mathcal{F}_{\it{L}}(\it{x+\epsilon}), \mathcal{F}_L^{C_t}) \geq \it{c_p}
?min?{?cos(FL?(x+?),FLCt??)+λ?∥FL?(x+?)?FLCt??∥2?},s.t.cos(FL?(x+?),FLCt??)≥cp?
Adaptive Iteration
??因为在等式中的约束条件只与损失函数的第一项有关,FIA应用以下自适应迭代来求解等式 : 第一步:我们通过设置
λ
=
0
\lambda=0
λ=0,开始只计算第一项损失项,直到满足约束。第二步:我们通过将
λ
\lambda
λ 设置为一个非零值(在文中设置为1),同时最小化两个损失项,以驱动
x
+
?
x+\epsilon
x+? 靠近目标类别
𝐶
𝑡
𝐶_𝑡
Ct?,同时保持满足约束。当
𝑥
+
?
𝑥+\epsilon
x+? 分类为
𝐶
𝑡
𝐶_𝑡
Ct?,其softmax 的最大预测概率比第二大的预测概率大与某一个阈值,我们重复第一步,只驱动第一项损失项通过设置
λ
=
0
\lambda=0
λ=0 只要 softmax 最大概率差距保持在阈值范围内。否则,就执行第二步,以此进行迭代过程。softmax距离是用来确保生成的对抗样本能够稳定的分类为目标类
C
t
C_t
Ct?。
Complete Scheme
??对抗的例子生成的基本方案可能仍然无法绕过陷阱检测由于几个原因:生成层和未知的检测层之间的不匹配,不规则的不可检测边界的陷阱防御,过于简单的凸区域假设特征表示分布的目标类别。
??为了解决这些问题,我们通过两个附加功能来增强了基本方案。第一个是准备阶段,使用基本方案生成一些对抗样本,以查询陷阱防御,以确定适当的生成层和其他生成参数。另一个是损失函数中的一个附加项,用于将对抗样本从在准备阶段检测到的对抗样本停留的陷阱区域引导出去。
Preparation Phase: 为了确定一个合适的生成层,我们为每个潜在的生成层使用基本方案生成少量的对抗性例子,从倒数第二层开始,向前移动,以查询陷阱防御。如果检测率低于一个阈值(即,当我们考虑找到一个合适的生成层时),我们停止并选择检测率最小的层作为生成层。由于倒数第二层通常作为陷阱防御的检测层,且基本方案效果相当好(见第6.7节),因此无需搜索多个层,就可以快速找到合适的生成层。
??一旦确定了生成层,我们就使用生成层的查询结果来调整等式中的目标
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt?? 和约束阈值
c
p
c_p
cp? 。如果生成的对抗样本都没有被检测出来的,则将使用具有原始
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt?? 和
c
p
c_p
cp? 的基本方案来生成对抗性示例。如果检出率足够高(高于预设阈值),这通常是由于在陷门防御对良性目标样本也有过高的假阳性率。这时我们从目标类的良性目标样本中收集足够的负样本(我们的实验评估为10个)。在这种情况下,负样本和未测试的目标类的良性目标样本被用来计算加权平均值,对于正样本有更多的权重(在我们的评估中是两倍)。这个加权平均值取代了基本方案中使用的
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt??。当生成对抗样本被检测出来时,就调整目标
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt??,使其远离它们如下:
Δ
=
F
L
C
t
?
E
x
∈
S
p
a
e
F
L
(
x
)
,
F
L
C
t
←
F
L
C
t
+
γ
d
r
Δ
∥
Δ
∥
2
,
\Delta = \mathcal{F}_L^{C_t} - \mathbf{E}_{x\in S_{pae}}\mathcal{F}_L(x),\\ \mathcal{F}_L^{C_t} \leftarrow \mathcal{F}_L^{C_t} + \gamma d_{r} \frac{\Delta}{\|\Delta\|_2},
Δ=FLCt???Ex∈Spae??FL?(x),FLCt??←FLCt??+γdr?∥Δ∥2?Δ?,
其中
S
p
a
e
S_{pae}
Spae? 是正对抗样本的集合,
d
r
d_r
dr?是生成的对抗例子的检出率,
γ
\gamma
γ 是一个正的加权参数(在我们的评估中为0.1)。
??一旦用等式确定了新的目标
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt??,我们可以在余弦相似度上确定一个新的约束边界
c
p
c_p
cp?,以包含负样本和尽可能多地排除正样本。更具体地说,我们计算了在该阶段使用新目标
F
L
C
t
\mathcal{F}_L^{C_t}
FLCt?? 查询的正样本和负样本(包括良性目标样本)的余弦相似度分布。我们预设了一个百分位数范围,[
𝑘
𝑛
𝑙
,
𝑘
𝑛
h
𝑘_{𝑛𝑙},𝑘_{𝑛?}
knl?,knh?] 百分位数([10,50]),以指定边界外负样本百分比的允许范围,以及一个阈值
𝑘
𝑝
𝑘_𝑝
kp? 百分位数(90)来指定边界外正样本的最小百分比。我们从负样本的余弦分布中得到对应的第
𝑘
𝑛
𝑙
𝑘_{𝑛𝑙}
knl?和第
𝑘
𝑛
h
𝑘_{𝑛?}
knh?百分位数的
𝑣
𝑘
𝑛
𝑙
𝑣_{𝑘𝑛𝑙}
vknl?和
𝑣
𝑘
𝑛
h
𝑣_{𝑘𝑛?}
vknh?,从正样本的分布中得到对应的第
𝑘
𝑝
𝑘_𝑝
kp?百分位数的
𝑣
𝑘
𝑝
𝑣_{𝑘𝑝}
vkp?。新的约束边界
c
p
c_p
cp? 的确定如下:
c
p
=
min
?
(
v
k
n
h
,
max
?
(
v
k
n
l
,
v
k
p
)
)
c_p = \min (v_{k_{nh}}, \max (v_{k_{nl}}, v_{k_p}))
cp?=min(vknh??,max(vknl??,vkp??))
Generation Phase
??在生成对抗性的例子时,我们将以下 drive-away 损失添加到基本方案的损失函数中在准备阶段,为了最小化与正对抗样本的余弦相似性:
l
a
w
a
y
(
F
L
(
x
)
)
=
∑
a
∈
S
p
a
e
cos
?
(
F
L
(
x
)
,
F
L
(
a
)
)
l_{away}(\mathcal{F}_L(x)) = \sum_{a \in S_{pae}} \cos (\mathcal{F}_L(x), \mathcal{F}_L(a))
laway?(FL?(x))=a∈Spae?∑?cos(FL?(x),FL?(a))
将上面的损失添加到优化损失中
l
(
F
L
(
x
)
,
F
L
C
t
)
=
?
c
o
s
(
F
L
(
x
+
?
)
,
F
L
C
t
)
+
λ
1
?
∥
F
L
(
x
+
?
)
?
F
L
C
t
∥
2
+
λ
2
?
∑
a
∈
S
p
a
e
cos
?
(
F
L
(
x
)
,
F
L
(
a
)
)
l(\mathcal{F}_L(x), \mathcal{F}_L^{C_t}) = -cos(\mathcal{F}_L(x+\epsilon),\mathcal{F}_L^{C_t})+\lambda_1 \cdot \| \mathcal{F}_L(x+\epsilon)-\mathcal{F}_L^{C_t} \|_2 + \lambda_2 \cdot \sum_{a \in S_{pae}} \cos (\mathcal{F}_L(x), \mathcal{F}_L(a))
l(FL?(x),FLCt??)=?cos(FL?(x+?),FLCt??)+λ1??∥FL?(x+?)?FLCt??∥2?+λ2??a∈Spae?∑?cos(FL?(x),FL?(a))
??制作对抗示例子的迭代与基本方案相似。一开始,我们只驱使等式的第一项损失通过设置
λ
1
=
λ
2
=
0
\lambda_1 = \lambda_2 = 0
λ1?=λ2?=0,直到约束被满足为止。然后,我们激活
λ
1
\lambda_1
λ1? 和
λ
2
\lambda_2
λ2?,以驱动
𝑥
𝑥
x 进入目标类别
𝐶
𝑡
𝐶_𝑡
Ct?,并远离特征空间中的积极例子。当
𝑥
𝑥
x 被分类为目标类别
𝐶
𝑡
𝐶_𝑡
Ct?时,
λ
1
\lambda_1
λ1? 将停止激活(设置为0)。当
λ
2
\lambda_2
λ2? 激活时,如果等式中的第一项,其值通过乘以一个因子(在我们的评估中为1.2)来调整与最后一次迭代相比,13会减少,或者如果rst增加,则除以另一个因子。