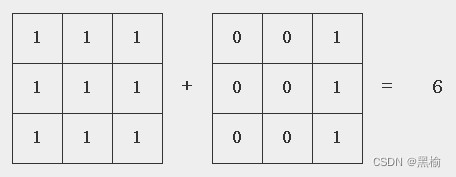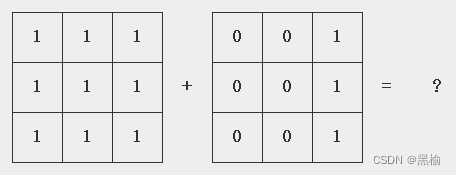
(A,B)---m*n*k---(1,0)(0,1)
移动距离和假设
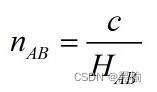
用神经网络分类A和B,把参与分类的A和B中的数字看作是组成A和B的粒子,设分类的过程就是让A和B中的粒子互相交换位置,寻找最短移动路径的过程。而熵H与最短移动距离和成正比,迭代次数n和熵H成反比。
对二值化图片移动规则汇总
每个粒子移动一次,位置重合不移动,0不动,单次移动距离恒为1.
按照移动距离和假设,如果两张图片不重合点的数量分别是a和b,则网络收敛的迭代次数反比于a+b,也就是网络的迭代次数是a+b的函数n=f(a+b)。因此对二值化图片实现一次收敛,就相当于完成了一次加法运算。这次就验证这一猜测,
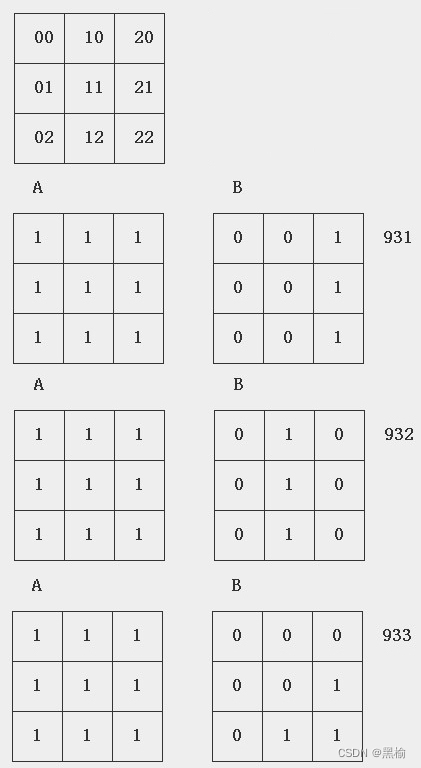
用神经网络分类A和B,让A中有9个1,B中有3个1,让A和B不断迭代直到收敛。统计迭代次数的平均值,并比较。
得到的迭代次数数据
| 931 | 932 | 933 | |
| δ | 迭代次数n | 迭代次数n | 迭代次数n |
| 5.00E-04 | 22166.65 | 22263.14 | 22501.15 |
| 4.00E-04 | 27290.48 | 27336.23 | 27418.16 |
| 3.00E-04 | 35639.73 | 35889.88 | 35563.93 |
| 2.00E-04 | 51890.25 | 52050.08 | 51690.69 |
| 1.00E-04 | 100158 | 99071.64 | 99730.86 |
| s | 6 | 6 | 6 |
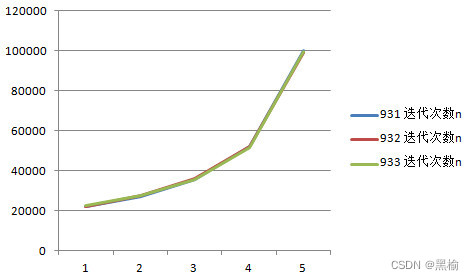
这几条曲线高度重合,因为他们的总移动距离s都是6.比如对931,931B中的3个1和A中的3个1位置重合。因此仅有A中的6个点需要移动。(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)。单次移动距离恒为1,因此总移动距离为6.
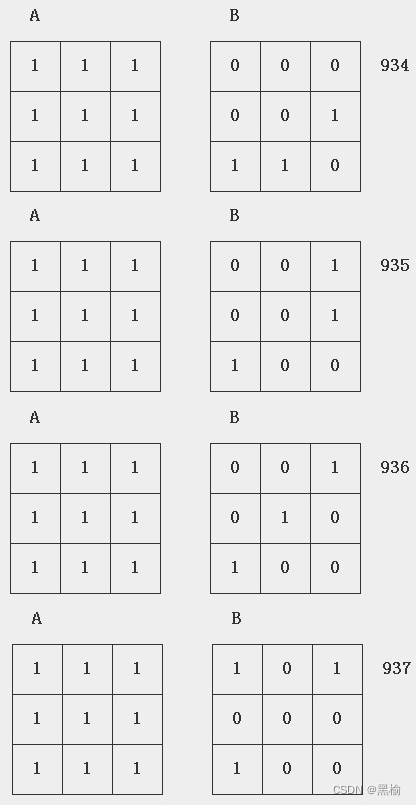
继续做934-937,进一步验证这一规律。得到数据
| 931 | 932 | 933 | 934 | 935 | 936 | 937 | |
| δ | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n |
| 5.00E-04 | 22166.65 | 22263.14 | 22501.15 | 22050.28 | 22313.26 | 22397.64 | 22429.29 |
| 4.00E-04 | 27290.48 | 27336.23 | 27418.16 | 27194.31 | 27369.58 | 27263.75 | 27367.36 |
| 3.00E-04 | 35639.73 | 35889.88 | 35563.93 | 35525.82 | 35512.64 | 35643.95 | 35821.85 |
| 2.00E-04 | 51890.25 | 52050.08 | 51690.69 | 52360.48 | 51986.76 | 52094.06 | 51873.35 |
| 1.00E-04 | 100158 | 99071.64 | 99730.86 | 98820.58 | 99440.88 | 99866.65 | 99778.57 |
| s | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
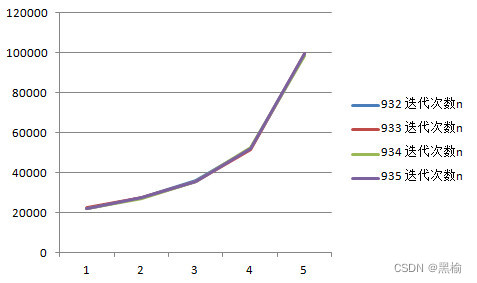
同样因为934-937的总移动距离也是6,因此他们和931-933的迭代次数曲线是高度一致的。
再将本次实验数据和前述实验数据做比较,
| 981 | 971 | 122 | 961 | 951 | 941 | 931 | |
| δ | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n | 迭代次数n |
| 5.00E-04 | 34219.01 | 28229.22 | 25862.05 | 25523.99 | 23904.73 | 22959.57 | 22166.65 |
| 4.00E-04 | 41899.68 | 34548.15 | 31524.1 | 30958.15 | 28978.03 | 27774.2 | 27290.48 |
| 3.00E-04 | 53474.56 | 44497.27 | 41011.36 | 40262.78 | 38252.24 | 35993.35 | 35639.73 |
| 2.00E-04 | 77797.83 | 64693.36 | 59270.11 | 59096.97 | 55426.48 | 52950.71 | 51890.25 |
| 1.00E-04 | 148175 | 123601.3 | 112397.9 | 113446.1 | 106880.8 | 101146.2 | 100158 |
| s | 1 | 2 | 3 | 3 | 4 | 5 | 6 |
可以清晰的看到迭代次数和总移动距离s之间的反比关系。
以收敛误差1e-4为例
| n | 148175 | 123601.3 | 112397.9 | 113446.1 | 106880.8 | 101146.2 | 100158 |
| a+b | 1 | 2 | 3 | 3 | 4 | 5 | 6 |
可以更直观的看到n=f(a+b)的数学关系,所以神经网络的迭代次数告诉我们