文章目录
一、基本概念
聚类是把一个数据对象划分成多个组或簇的过程,使得簇内对象相似度很高,而簇间对象相似度很低。
聚类属于无监督分类方式。
主要得的聚类方法主要有:基于划分的方法,基于层次的方法,基于密度的方法,基于网格的方法,基于模型的方法。
二、基于划分的方法
1.划分的思想
给定一个有n个数据对象的集合,基于划分的方法会构建数据的k个分组,其中每个分组表示一个簇。
对于给定的分组数k,算法会首先给出一个初始的分组方法,然后通过不断迭代的方法改变分组,使得同一组内的距离越来越近,不同组间的距离越来越远。
基于划分思想的算法有k-means,k-中心点。
如果想达到全局最优,则需要穷举所有可能的划分,计算量极大,可以采用启发式方法,比如k-means,k-中心点,逐渐的提高划分质量,逼近局部最优解。
2.K-means
算法步骤:
(1)在n个数据对象的集合中,随机的选择k个点,分别做为k个簇的中心。
(2)分别计算其余点和k个簇中心点的距离,离哪一个簇中心点最近,就将其划分到对应的簇。
(3)对于每个簇,重新计算簇中心点。
(4)不断循环下去,直至达到算法终止条件。
初始质心的选择:
最常见的方法是随机的选择初始质心,为了得到更好的结果可以多次运行算法。
距离度量:
对欧氏空间内的点使用欧几里得距离度量
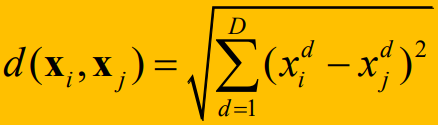
对于文档使用余弦相似性度量
簇中心计算方法:
在步骤三中,如何重新计算簇中心呢,取簇中所有对象每一个维度的算术平均值。
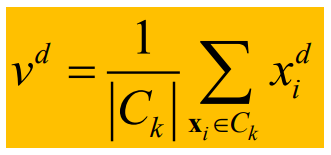
其中d代表维度,v代表新的簇中心坐标点,|Ck|代表簇内点的个数。
目标函数:聚类的目标函数依赖于点到簇的质心的邻近性,使用误差的平方和(SSE)作为度量聚类质量的目标函数。
定义如下:
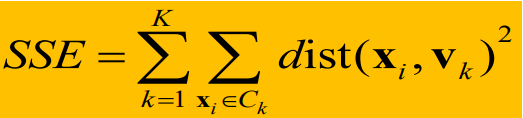
首先求每个簇中,每个数据点xi到簇中心vk的距离平方和,然后把所有簇的距离和再求和。
步骤(2)和步骤(3)就是在最小化SSE,但是只能确保找到的是局部最优解。
算法停止条件:
(1)设定迭代次数。
(2)簇类中心不再变化。
(3)前后两次聚类结果的SSE变化很小。
优缺点:
优点:K-means的复杂度O(tkn),其中n是数据对象的个数,k是簇数,t是迭代的次数,通常t,k都远远小于n
缺点:需要事先给出k的值,不能处理噪声数据和孤立点,鲁棒性较差,不适合发现非球形簇。
3.k-中心点算法
由于K-means不能处理噪声数据和离群点,k-中心点算法是对k-manes的改进,改进之后,能够能够处理噪声点和离群点。
PAM是一种k-中心点算法。
改进点如下:
在更新簇中心时,不是计算簇内所有点的算术平均值做为新的簇中心点,而是选择离所有点距离最小的点做为新的中心点。
PAM使用绝对误差标准来衡量聚类质量
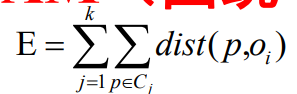
其中k代表k个聚类,p代表簇Ci中非代表对象,Oi代表簇Ci中的代表对象。
步骤如下:
(1)在n个数据对象的集合中,随机的选择k个点,分别做为k个簇的中心。
(2)分别计算其余点和k个簇中心点的距离,离哪一个簇中心点最近,就将其划分到对应的簇。
(3)对于每个簇,将簇中每个点都依次做为代表对象,然后选择绝对误差标准最小的点做为簇中心点。
(4)不断循环下去,直至达到算法终止条件。
三、基于层次的方法
基于层次的方法可以分为凝聚与分类。
凝聚层次分类:自底向上,刚开始将每个对象单独做为一个簇,然后将相似的簇逐渐合起来,直到达到终止条件。
分类层次聚类:自顶向下,刚开始所有对象都在一个簇中,然后不断的分裂,直到达到终止条件。
1.簇间距离:
无论时哪一种方法,都需要度量簇间的距离,根据度量方法的不同,将层次聚类分为单连接,全连接和平均连接。
其中单连接采用的是最小距离
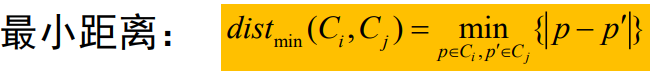
全连接采用的是最大距离
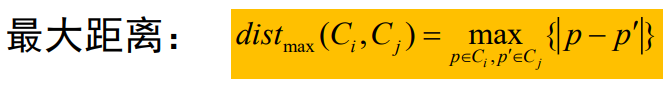
平均连接采用的是平均距离
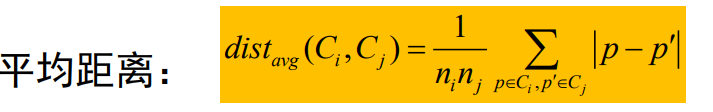
除此之外,还有均值距离

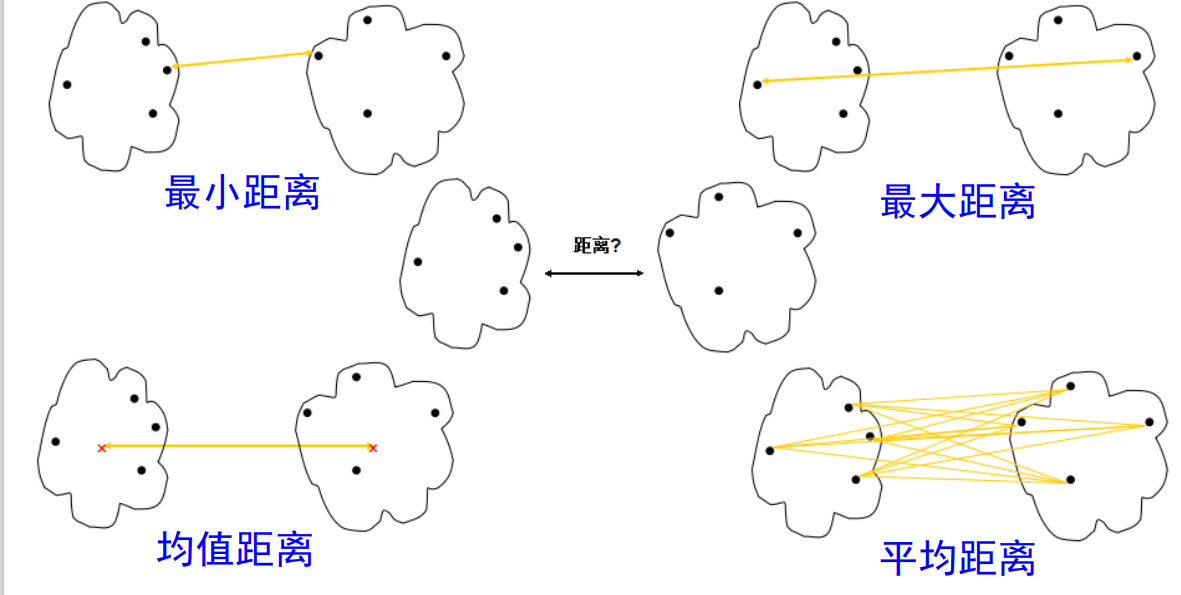
最小距离:代表不同簇之间最近的两个点之间的距离
最大距离:代表不同簇之间最远的两个点之间的距离
均值距离:代表不同簇中心点之间的距离
平均距离:代表不同簇所有点之间距离的平均值
以上四种距离的示意图如下:
2.AGNES
该算法使用单连接方法和距离矩阵,然后合并距离最小的相异点,继续计算新的距离矩阵,继续合并距离最小的相异点。直到达到簇的数目。
一个实例如下:
二维空间中有以下五个点,使用单连接算法进行聚类。
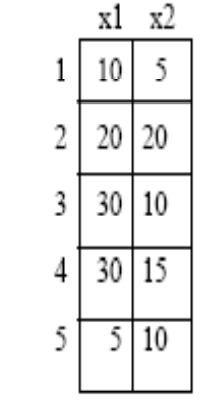
第一步:计算距离矩阵
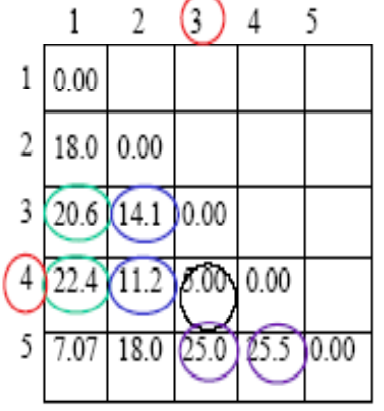
可以得到,3和4之间的距离5是最小的,所以将3和4聚成一类。
第二步:重新计算距离矩阵
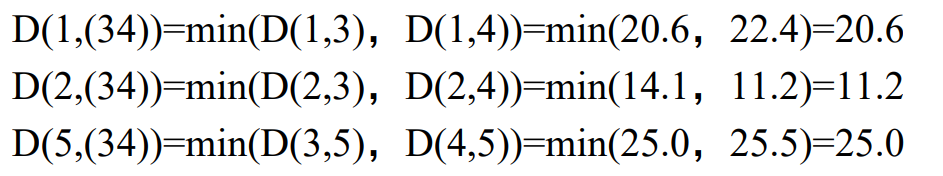
原来簇1,2,5之间的距离不变,改变的是1,2,5和簇(3,4)之间的距离。更新后的距离矩阵如下
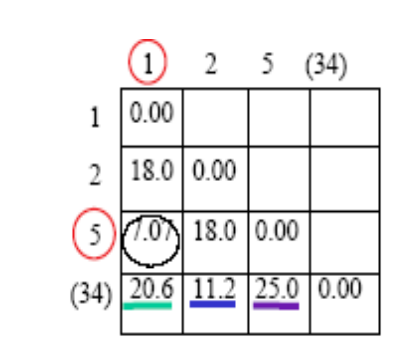
可以得到簇1和簇5之间的距离1.07是最小的,所以把1和5聚成一类。
第三步:重新计算距离矩阵
需要计算簇2和簇(1,5)和簇(3,4)这三种之间的距离。更新之后的距离矩阵如下:
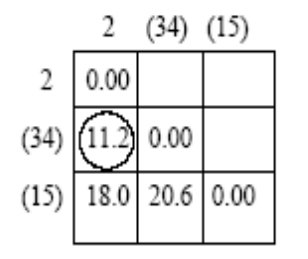
可以得到簇2和簇(3,4)之间的距离最小,所以将簇2和簇(3,4)聚成一类。
第四步:重新计算距离矩阵
只需要计算簇(2,3,4)和簇(1,5)
之间的距离。
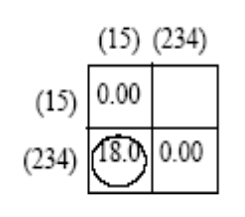
最后将簇(1,5)和簇(2,3,4)聚成一类。
单连接算法的距离都是指的最小距离。
如果设置了终止条件,在中途就会退出。
用树状图将其可视化描述出来如下:

用户可以定义希望得到的簇数作为一个终止条件。
最小最大度量对于离群点和噪声数据很敏感。
使用均值距离和平均距离是一种折中的方案,可以克服离群点敏感性问题。
四、基于密度的方法
基于划分和层次的方法都旨在发现球状簇,不能发现任意形状的簇。而基于密度聚类的方法可以发现任意形状的簇,可以把簇看作数据空间中被稀疏区域分开的稠密区域。
1.DBSCAN算法
EPS邻域:某个点指定半径为r的圆区域。
Minpts:最少包含的点的个数。
核心点:该点的邻域内的点的个数超过指定阈值MinPoints。
边界点:边界点是位于核心点内的点,同时,该点的EPS邻域内,没有新的,未被标记的点。
离群点:既不是边界点也不是核心点。
直接密度可达:给定一个对象集合D,如果p在q的Eps邻域内,而q是一个核心对象,则称对象p从对象q出发时是密度可达的。
密度可达:如果存在一个对象链,p1,p2,…,pn,p1 = q,pn = p,且对于任意的pi,pi+1是直接密度可达的,则对象p是从对象q出发是密度可达到。
密度相连:如果存在一个对象O,使得对象p和对象q都是从O密度可达的,那么对象p和对象q是密度相连的。
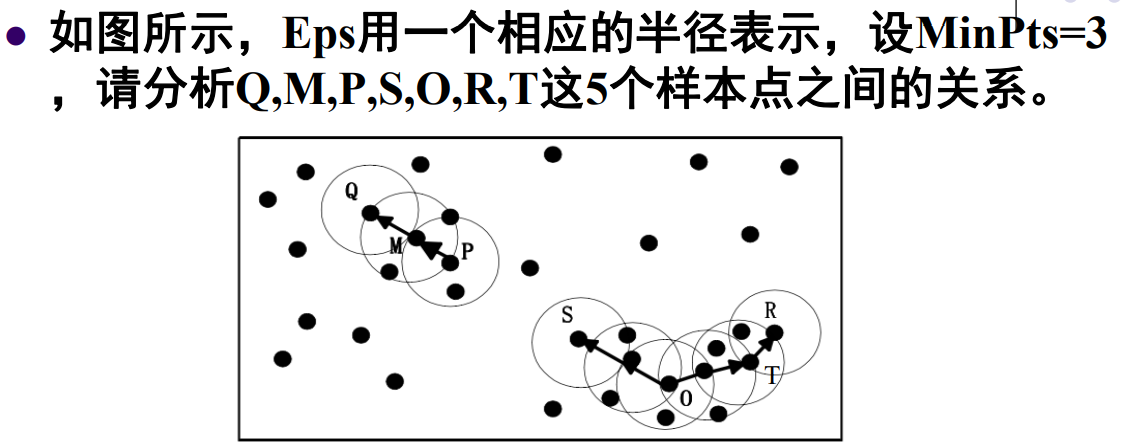
由于MinPts = 3,
M,P是核心点,Q不是核心点。
O,T是核心点,S,R不是核心点。
由于M在P的邻域内,P是核心点,所以M从P出发直接密度可达。
由于Q在M的邻域内,M是核心点,所以Q从M出发直接密度可达,Q从P出发密度可达。
同理,S从O出发密度可达,R从O出发密度可达,所以S和R密度相连。
算法步骤:

可以看到,DBSCAN会找到最大密度相连的点的集合。
优点:
基于密度定义,对噪声不敏感,可以发现任意形状的簇
缺点:
当聚类密度不均匀时,聚类质量不好。
当数据量较大,数据维度较高时,容易内存溢出。
五、聚类评估
聚类评估主要包括如下任务:
估计聚类趋势,确定数据集中的簇数
测定聚类质量
1.估计聚类趋势
只有当数据集中存在非随机结构,聚类分析才有意义。
(1)如果聚类误差随着聚类类别数量的变化而变化不显著,说明数据是随机分布的,即不存在非随机结构。
(2)霍普金斯统计量:
第一步,均匀在数据集D中抽取n个点p1,p2,p3,…,pn。对于其中每一个点,都计算数据集D中离该点最近的点,并记录其距离为xi。
第二步,均匀在数据集D中抽取n个点q1,q2,q3,…,qn。对于其中每一个点,都计算数据集D中离该点最近的点,并记录其距离为yi。
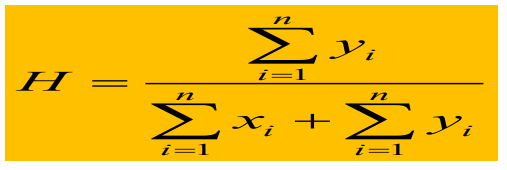
如果D为随机分布,H大约为0.5
如果聚类趋势明显,则H的值接近于1或0
一般H>0.75,则可以聚类的置信度90%
2.聚类簇数的确定
经验方法:簇数p大约为
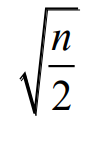
拐点法:绘制簇内方差和关于簇数的曲线,拐点的簇数就是设置的簇数。
交叉验证法:对于给定的数据集分成m份,用m-1份构建聚类模型,用剩下的一份检验聚类的质量,选择聚类质量最高的聚类模型,并使用其K作为聚类簇数。
3.聚类质量的测定:
外在方法:有监督的方法,熵,纯度,精度,召回率,F度量。具体公式看教材。
内在方法:无监督方法,考察簇间的分离情况和簇内的紧凑情况。
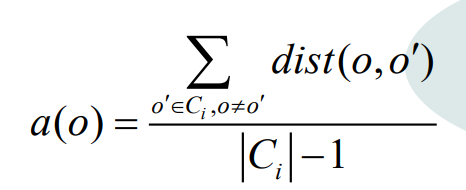
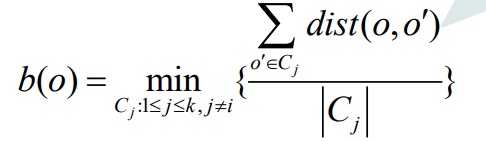
轮廓系数S(O)
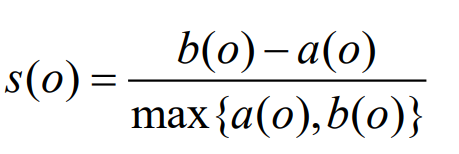
其中数据集D被分成了k个簇,分别为C1,C2,C3,…,Ck,对于每一个数据对象O
a(O)代表着O与O所在的簇其他所有点的平均距离。
b(O)代表着O与O所不在的其他所有簇的簇间最小平均距离。
a(O)的值反映簇内的紧凑性,值越小越紧凑。b(O)的值反映簇间的分离程度,值越大越分离。
当o簇的轮廓系数S(O)值越接近于1,O所在的簇是紧凑的,并且远离其他簇。