
数据预处理与数据工程是机器学习发展至今的一大瓶颈,好的数据预处理可以极大提升机器学习预测的准确性。然而现在实践中的数据预处理与数据工程主要是基于人的经验,并没有一个可以依赖的强有力算法。本篇论文提出了一个编码数据的方式,自动进行数据预处理与数据工程,节省人力的同时也在实验中取得不错效果。
问题描述
构建机器学习的训练数据集十分困难,这主要有3个原因。为了方便描述,这里以论文中的STUDENT数据集为例。该数据集是本篇论文生成的数据,包含3个表格:Expenses, Order Info和Price Info。现在我们要预测Total Expenses,我们尝试构建一个机器学习模型用于实现这一预测目标。
首先,确定一个问题的相关特征是困难的。我们希望预测的属性Total Expenses究竟与哪些属性有关,我们并不能提前知道,它可能与school Name有关,可能与Name有关,但在构建模型并获得实验结果之前这些都是不可知的。
其次,在确定了相关特征后,找到那些含有相关特征的数据集是困难的。在这个例子中我们已经给出了可供选择的数据,这个问题的严重性并不明显。但大部分情况下,我们并不知道我们需要的指标在哪些数据集中可以找到。例如在金融领域,人们常常需要预测股票未来涨势。当然,我们可以使用历史的股票价格来进行预测,但这大多数情况并不能取得很好的效果。一些炒股大佬,可能会选择从金融方面的数据集获取一些数据信息,结合大盘历史信息获得用于机器学习的特征。
最后,确定相关数据的连接方式是困难的。回到STUDENT的例子中,我们可以简单粗暴地将所有表格连接到一起,用以获得更加全面的特征。当问题更复杂时,key与foreign key的选择将成为一个严峻问题。表格的连接方式并不唯一,选择什么样的连接方式成为一个问题。

现有方法与不足
针对上述问题,已有方法包括:Base Table、Full Table、Full Table + Feature Engineering三种。
| 方法 | 描述 | 不足 |
|---|---|---|
| Base Table | 只使用包含预测标签的表格作为训练的数据 | 不准确 |
| Full Table | 将尽可能多的表格连接在一起 | 开销大 |
| Full Table + Feature Engineering | 在full table上运行特征工程的算法 | 开销大 |
本篇论文核心观点
Leva使用graph表示数据集中的每一行数据,然后通过graph embedding将每一行表示成一个向量,用于下游ML任务的特征。整个流程中有2个阶段:Graph construction 和 Embedding construction。其中Graph construction阶段中为了降低时间复杂度,在图中引入Value Node节点,用于加速图的构建;而在Embedding construction阶段,论文提出了2个方法用于应对现实中内存不够的情况:Random Walk和Matrix Factorization。
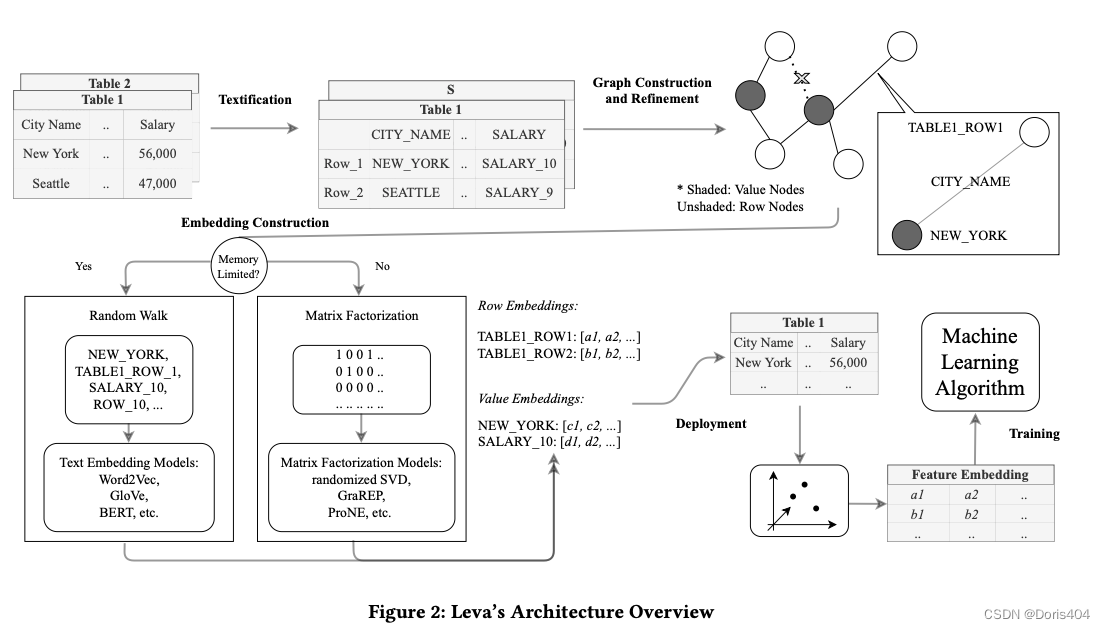
本篇论文提出方法操作
Graph construction
直观的想法是,根据每行数据的相似性构建临界矩阵或相似矩阵,但论文中指出这种构建方式太过缓慢,时间复杂度是
O
(
M
N
2
)
O(MN^2)
O(MN2)1。因而引入Value Node用来加速图构建,将图构建的时间复杂度降到
O
(
M
N
)
O(MN)
O(MN)。

Embedding construction
论文提出2种嵌入方法:Random Walk和Matrix Factorization。其中Random Walk的实现即是先随机游走得到一个结果:row-row-row,然后在使用NLP领域的方法将对这个序列进行编码,论文用的是Word2Vec。Matrix Factorization则采用SVD分解那一套,论文中使用的是randomized SVD。

本篇论文没有提供代码。
为什么有效
2个原因保证了这种编码方式是有效的。
其一,Graph 后 embedding的框架使得编码之后每行数据的表示向量之间的距离远近含有其在Graph上是否接近的信息,即:Graph->embedding的映射信息损失可接受。同时原始数据到graph的转化,在原有信息的基础上引入了similarity matrix用于衡量2行数据的相似性。
其二,多余的信息表示,可以通过下游任务的训练去除。去除的效果在论文中有实验证明2。Figure 3是实验结果,其横坐标代表引入的噪音,纵坐标表示从
?
a
l
l
\epsilon_{all}
?all?到
?
c
l
e
a
n
\epsilon_{clean}
?clean?的映射好坏,其指标为
R
2
R^2
R23。从实验结果不难看出,噪音增加并不会影响
?
a
l
l
\epsilon_{all}
?all?到
?
c
l
e
a
n
\epsilon_{clean}
?clean?映射的准确性。
