参考:D2L
学习笔记
前言
DL Advance
- Dropout
- ReLu
- MaxPooling

? 在卷积神经?络中,组合使?卷积层、?线性激活函数和c池化层。
? 为了构造?性能的卷积神经?络,通常对卷积层进?排列,逐渐降低其表?的空间分辨率,同时增
加通道数。
? 在传统的卷积神经?络中,卷积块编码得到的表征在输出之前需由?个或多个全连接层进?处理。
LeNet
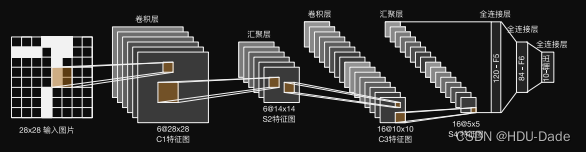

卷积层:学习图片空间信息
池化层:降低模型复杂度,泛化模型
全连接层:转换到类别空间
AlexNet
更大更深的LeNet
8 layers:
- 5 Conv layers
- 3 FC hidding layers
- 1 FC out layers
- 更大的池化窗口,使用最大池化层
- 更大的卷积核和步长,因为图片
- 新加了3层卷积层
- 更多的输出通道
- 1000类输出
- 隐藏层从120到4096
more details
- 激活函数从sigmoid变到ReLu(缓减梯度消失)
- 隐藏全连接层后加入了丢弃层
- 数据增强
VGG
更深更大的AlexNet
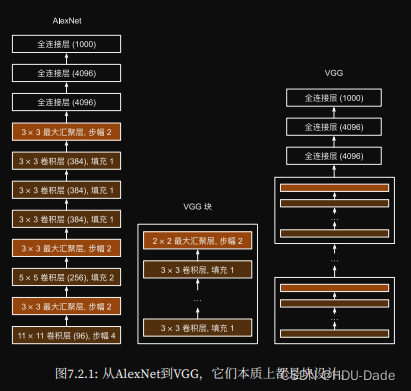
- 3*3 Conv 深但窄 效果更好
- 多个可重复使用的VCG块后接全连接层
- 不同次数的重复块得到不同架构,不同的卷积快个数和超参数可以得到不同复杂度的变种
NiN
全连接层:参数爆炸
LeNet 16x5x5x120= 48k
AlexNet 256x5x5x4096= 26M
VGG 512x7x7x4096= 102M
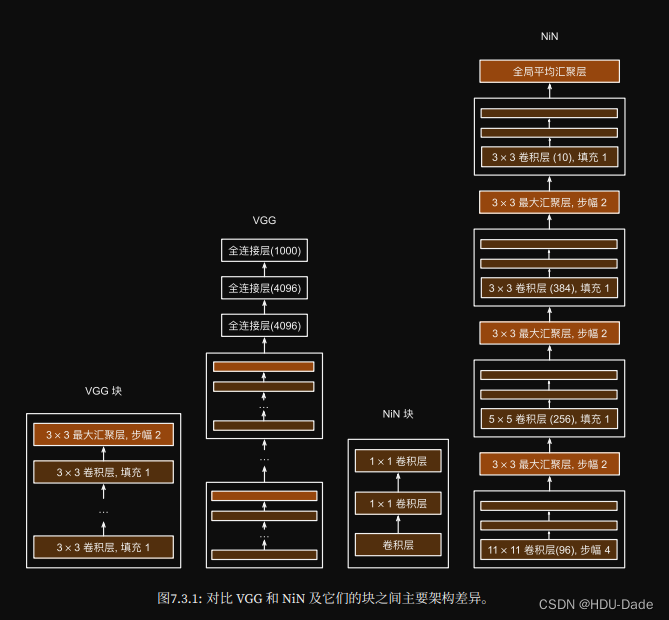
NiN块
- 一个卷积层后跟两个全连接层
- 无全连接层
- 交替使用NiN块和步幅为2的最大池化层
- 逐步减小高宽和增大通道数
- 最后使用全局平均池化层得到输出
- 其输入通道数是类别数
GoogLeNet
思考:最好的卷积层超参数?
1×1 3×3 5×5 Max pooling Multiple 1×1
能不能全都要?
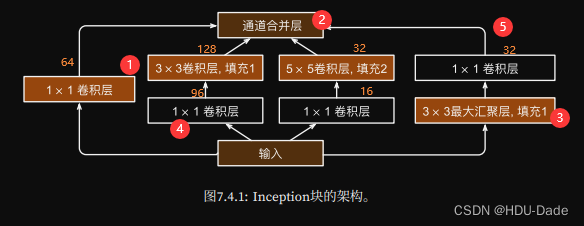
Inception块
4个路径从不同层面抽取信息,然后在输出通道维合并
- 使用不同大小的卷积层
- 跟输入等同高宽
- 使用池化层
- 降低通道数来控制模型复杂度
- 总共256通道 一半给3×3 剩下一半给1×1 再分给5×5和1×1
- 黑色1×1Conv 变化通道数
橙色1×1Conv 抽取图像信息
橙色3×3 5×5 Conv MaxPool抽取空间信息- 每条路上通道数可能不同
与单3×3或5×5 Conv相比 Inception块有更少的参数个数和更低的计算复杂度
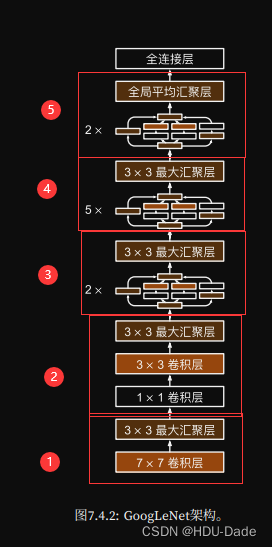
Details:
Stage3:通道分配不同 输出通道增加
Stage4:增加通道数,增加通道数
Stage5:增加通道数,1024维特征输出
ResNet
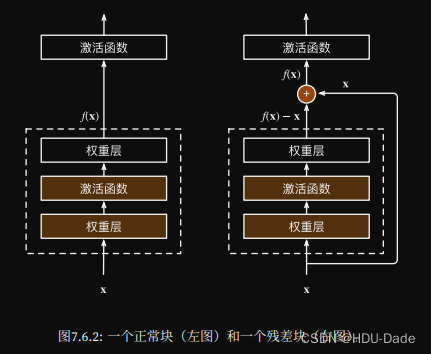
残差块:
- 每个附加层都应该更容易地包含原始函数作为其元素之一
- 堆叠层数的同时不会增加模型的复杂度
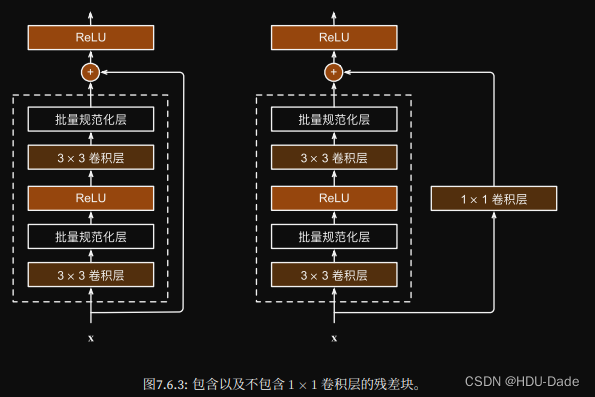
- 不包含1×1:输入加在了叠加层的输出上面
- 包含1×1:改变通道数,再加入到叠加层的输出上面
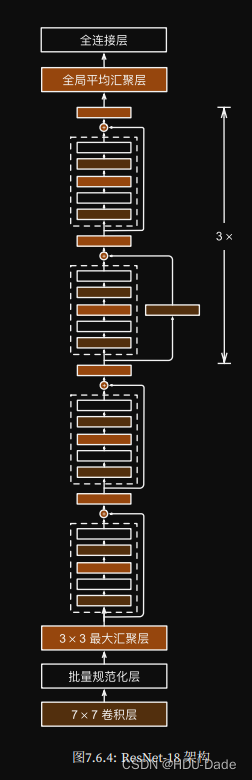
- 架构类似于VGG和GoogLeNet,但是替换成了ResNet块(ResNet块的每个卷积层后增加了批量归一化层)
- ResNet的前两层和GoogLeNet中的一样,也分成了5个stage:在输出通道数为64、步幅为2的7 * 7卷积层后,接步幅为2的3 * 3的最大汇聚层
- GoogLeNet在后面接了4由Inception块组成的模块;ResNet使用了4个由残差块组成的模块,每个模块使用若干个同样输出通道数的残差块,第一个模块的通道数同输入通道数一致;由于之前已经使用了步幅为2的最大汇聚层,所以无需减小高和宽;之后每个模块在第一个残差块里将上一个模块的通道数翻倍,并将高和宽减半
- 通过配置不同的通道数和模块中的残差块数可以得到不同的ResNet模型
Details:
残差连接(Residual Connection)
- 将乘法运算变成加法运算
- 将函数分解为:一个简单的线性项和一个复杂的非线性想v
- 避免梯度消失
y
=
f
(
x
)
y = f(x)
y=f(x)
y
‘
=
f
(
x
)
+
g
(
f
(
x
)
)
y‘ = f(x) + g( f(x) )
y‘=f(x)+g(f(x)) 表示使用堆叠的方式对原有的模型进行加深之后的模型
y
‘
′
=
f
(
x
)
+
g
(
f
(
x
)
)
y‘' = f(x) + g( f(x) )
y‘′=f(x)+g(f(x)) 表示使用残差连接的方式对原有的模型进行加深之后的模型输出
这两项来说,就算第二项的值比较小,但还是有第一项的值进行补充(大数加上一个小数还是一个大数,但是大数乘以一个小数就可能变成小数)
