[人工智能]机器学习实战：回归

线性回归基本问题

线性回归模型函数与损失函数

• 问题
  m个样本数据，每个样本对应n个特征及一个输出，针对样本输入$x_i$，其输出预测$\widehat{y_i}$如何计算？
• 模型函数
  $$h_{\theta }(x_0,x_1,...,x_n)=\sum _{i=0}^n{\theta }_i?x_i$$
  其中$x_0=1$.写成矩阵形式，$h_{\theta }(X):(m,1)$、$X:(m,n)$、$\theta :(n,1)$形矩阵
  $$h_{\theta }(X)=\sum _{i=0}^{n}x?\theta$$
• 损失函数
  $$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\sum _{i=1}^m(h_{\theta }(x_0,x_1,...,x_n)?y_i{)}^2$$$$J(\theta )=\frac{1}{2}(X\theta ?Y{)}^T?(X\theta ?Y)$$

线性回归算法

• 梯度下降
  $$\theta =\theta ?\alpha X^T(X\theta ?Y)$$

• 最小二乘法
  $$\theta =(X^{T}X{)}^{?1}{X}^{T}Y$$

• 判断回归效果
  计算相关系数R:预测序列$\hat{y}$与真实值序列$y$的匹配程度

标准线性回归

数据集：ex0.txt

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.font_manager import FontProperties

font = FontProperties(fname=r"C:\Windows\Fonts\STFANGSO.TTF")
file_name = "D:\深度学习\机器学习\8回归\ex0.txt"


"""
函数名：load_dataset
函数说明：加载数据
input:
    file_name:数据路径
output:
    data_mat:特征集
    label_mat:标签集
"""
def load_dataset(file_name):
    numFeat = len(open(file_name).readline().split('\t'))-1  # 特征数
    dataMat = []; labelMat = []
    fr = open(file_name)
    for line in fr.readlines():
        linarr = []
        currentline = line.strip().split('\t')
        for i in range(numFeat):
            linarr.append(float(currentline[i]))  # float必须的，否则数据为str类型
        dataMat.append(linarr)
        labelMat.append(float(currentline[-1]))
    return dataMat,labelMat

def standRegression(dataMat,labelMat):
    data_x = np.mat(dataMat)
    data_y = np.mat(labelMat).T
    xTx = data_x.T * data_x
    if np.linalg.det(xTx) == 0.0:
        print('矩阵不可逆')
    ws = xTx.I*(data_x.T*data_y)
    return ws

if __name__ == '__main__':
    dataMat,labelMat = load_dataset(file_name)
    dataArr = np.array(dataMat)
    labelArr = np.array(labelMat)
    dataArr = dataArr[:,1]
    ws = standRegression(dataMat,labelMat)
    print(np.shape(ws))
    yHat = (np.mat(dataMat)*ws).flatten().A[0]
    fig = plt.figure()
    axs = fig.add_subplot(111)
    axs.scatter(dataArr,labelArr,label='真实')
    axs.plot(dataArr,yHat,label="预测")
    plt.xlabel("x")
    plt.ylabel('y')
    plt.legend(prop=font)
    plt.show()

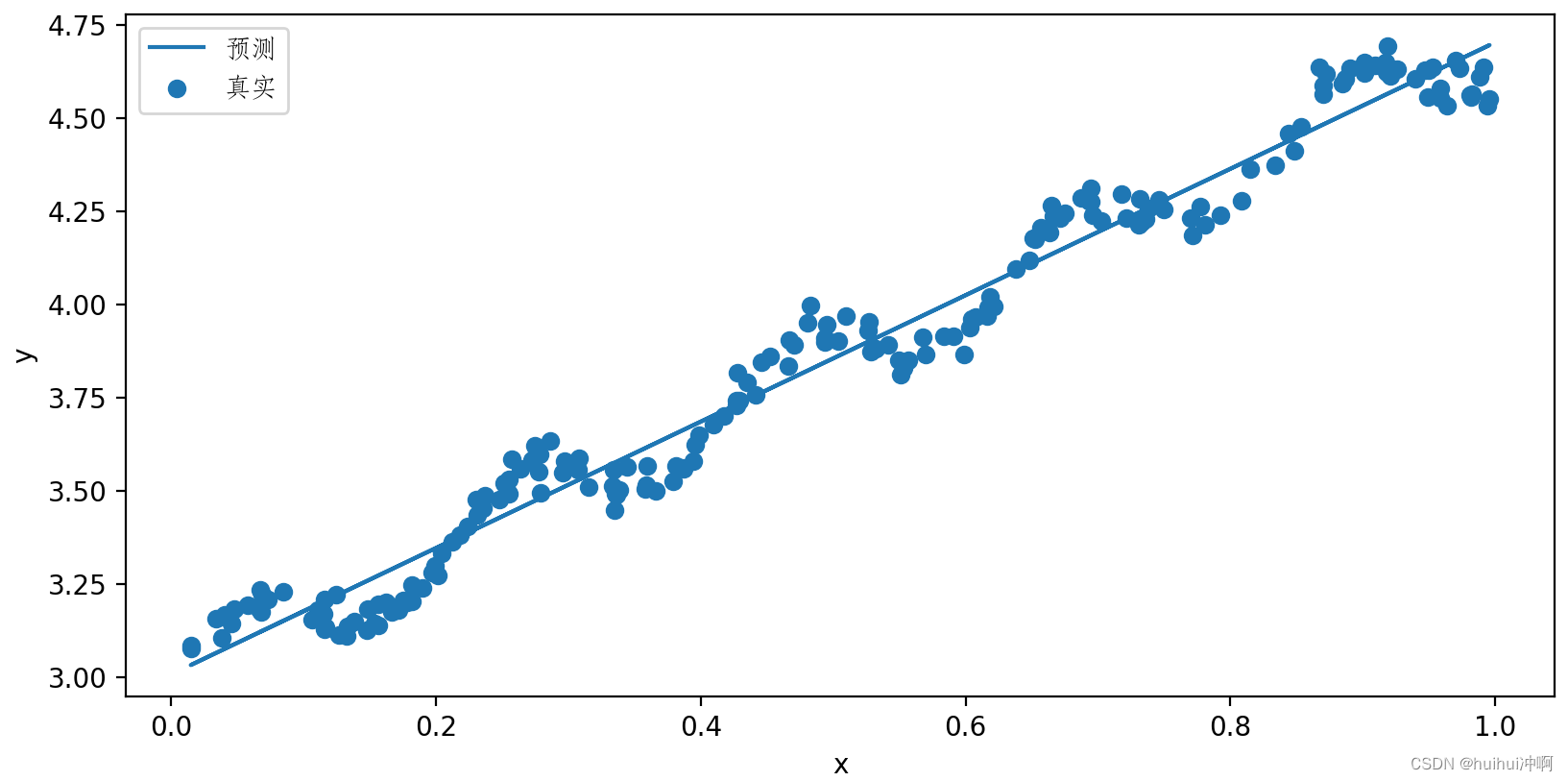
局部加权线性回归

线性回归的一个问题是有可能出现欠拟合现象，因为它求的是具有最小均方误差的无偏估计。显而易见，如果模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。 其中的一个方法是局部加权线性回归（Locally Weighted Linear Regression，LWLR）。在该算法中，我们给待预测点附近的每个点赋予一定的权重，算法解出回归系数w的形式如下：
$$\hat{\theta }=(X^T\omega X{)}^{?1}{X}^T\omega Y$$
LWLR使用“核”（与支持向量机中的核类似）来对附近的点赋予更高的权重①。核的类型可以自由选择，最常用的核就是高斯核，高斯核对应的权重如下：
$$\omega (i,i)=exp(\frac{|x_i?x|}{?2k^2})$$
构建了一个只含对角元素的权重矩阵w，并且点x与x(i)越近，w(i,i)将会越大，式包含一个需要用户指定的参数k，它决定了对附近的点赋予多大的权重。k越大，用于训练模型的数据点的数量越多；k越小，用于训练模型的数据点的数量越少，容易过拟合。
数据集：ex0.txt

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

font = FontProperties(fname=r"C:\Windows\Fonts\STFANGSO.TTF")
"""
函数说明：加载数据
Input:
    file_path:文件路径
Outout:
    dataMat
    labelMat
"""
def load_dataset(file_path):
    numFeat = len(open(file_path).readline().split('\t'))-1
    dataMat = []
    labelMat = []
    fr = open(file_path)
    for line in fr.readlines():
        line_arr = []
        current_line = line.strip().split('\t')
        for i in range(numFeat):
            line_arr.append(float(current_line[i]))
        dataMat.append(line_arr)
        labelMat.append(float(current_line[-1]))
    return dataMat,labelMat

"""
函数说明：LWLR计算权重
Input：
    test_point: 测试点
    k
    dataMat
    labelMat
Returns:
    ws
"""
def LELR(test_point,k,dataMat,yMat):
    m = np.shape(dataMat)[0]
    w = np.mat(np.eye((m)))
    for j in range(m):
        diffMat = test_point - dataMat[j,:]
        w[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = dataMat.T*w*dataMat
    if np.linalg.det(xTx) == 0.0:
        print("矩阵不可逆")
        return
    ws = xTx.I*dataMat.T*w*yMat
    return ws
"""
函数说明：计算出yHat:
Input:
    dataMat
    labelMat
Output:
    yHat
"""
def caluc_yhat(test_arr,dataMat,yMat,k):
    n = np.shape(test_arr)[0]
    yHat = np.zeros(n)
    for i in range(np.shape(test_arr)[0]):
        test_point = test_arr[i]
        ws = LELR(test_point,k,dataMat,yMat)
        yHat[i] = test_point*ws
    return yHat
"""
函数说明：不同k值局部加权回归的效果图
Input:
    k_list
    filepath"""
def k_plot(k_list,filepath):
    dataMat,labelMat = load_dataset(filepath)
    dataMat = np.mat(dataMat)
    yMat = np.mat(labelMat).T
    strInd = dataMat[:,1].argsort(0)
    xSort = dataMat[strInd][:,0]
    print(np.shape(xSort[:,0]))
    fig,axs = plt.subplots(nrows=3,ncols=1)
    print(np.shape(dataMat[:,1]))
    print(np.shape(yMat.flatten().A[0]))
    for i in range(len(k_list)):
        yHat = caluc_yhat(test_arr=dataMat,dataMat=dataMat,yMat=yMat,k = k_list[i])
        axs[i].scatter(np.array(dataMat[:,1]),yMat.flatten().A[0],s=3)
        axs[i].plot(xSort[:,1],yHat[strInd],linewidth=1.5,color='orange')
        axs[i].set_title("k="+str(k_list[i]))
    plt.tight_layout()
    plt.show()

filepath = "D:\深度学习\机器学习\8回归\ex0.txt"
k_list = [1.0,0.01,0.003]
k_plot(k_list,filepath)

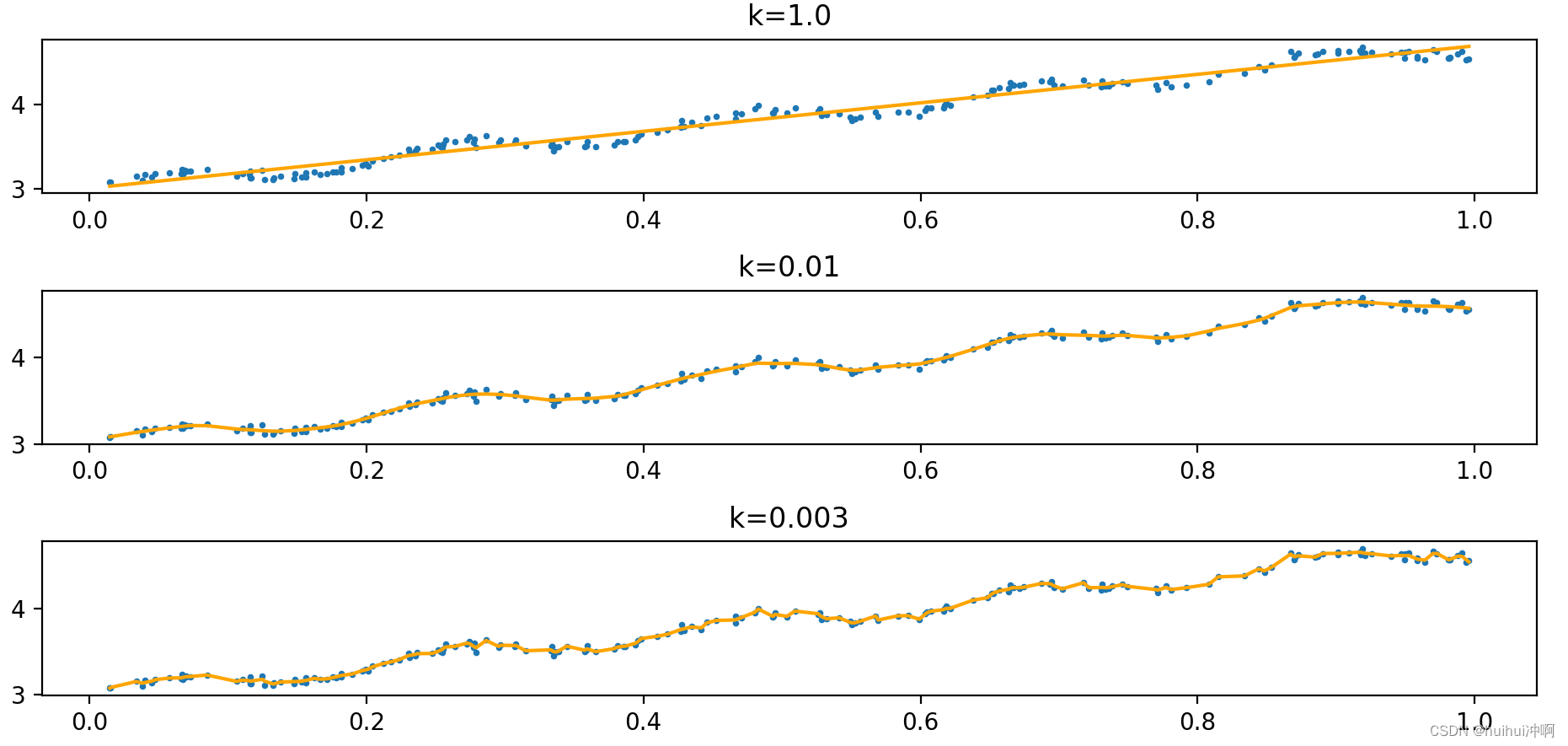
随着样本点与待预测点距离的递增，权重将以指数级衰减 。输入参数k控制衰减的速度。当k = 1.0时权重很大，如同将所有的数据视为等权重，得出的最佳拟合直线与标准的回归一致。使用k = 0.01得到了非常好的效果，抓住了数据的潜在模式。下图使用k = 0.003纳入了太多的噪声点，拟合的直线与数据点过于贴近，出现过拟合现象。
局部加权线性回归也存在一个问题，即增加了计算量，因为它对每个点做预测时都必须使用整个数据集。

预测鲍鱼年龄

数据集：abalone.txt

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

font = FontProperties(fname=r"C:\Windows\Fonts\STFANGSO.TTF")
"""
函数说明：加载数据
Input:
    file_path:文件路径
Outout:
    dataMat
    labelMat
"""
def load_dataset(file_path):
    numFeat = len(open(file_path).readline().split('\t'))-1
    dataMat = []
    labelMat = []
    fr = open(file_path)
    for line in fr.readlines():
        line_arr = []
        current_line = line.strip().split('\t')
        for i in range(numFeat):
            line_arr.append(float(current_line[i]))
        dataMat.append(line_arr)
        labelMat.append(float(current_line[-1]))
    return dataMat,labelMat

"""
函数说明：LWLR计算权重
Input：
    test_point: 测试点
    k
    dataMat
    labelMat
Returns:
    ws
"""
def LELR(test_point,k,dataMat,yMat):
    m = np.shape(dataMat)[0]
    w = np.mat(np.eye((m)))
    for j in range(m):
        diffMat = test_point - dataMat[j,:]
        w[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = dataMat.T*w*dataMat
    if np.linalg.det(xTx) == 0.0:
        print("矩阵不可逆")
        return
    ws = xTx.I*dataMat.T*w*yMat
    return ws
"""
函数说明：计算出yHat:
Input:
    dataMat
    labelMat
Output:
    yHat
"""
def caluc_yhat(test_arr,dataMat,yMat,k):
    n = np.shape(test_arr)[0]
    yHat = np.zeros(n)
    for i in range(np.shape(test_arr)[0]):
        test_point = test_arr[i]
        ws = LELR(test_point,k,dataMat,yMat)
        yHat[i] = test_point*ws
    return yHat

file_path = "D:\深度学习\机器学习\8回归\\abalone.txt"
dataMat,labelMat = load_dataset(file_path)
dataMat = np.mat(dataMat)
labelMat = np.mat(labelMat).T
"""
函数说明：计算损失值
Input:
    yTrue - 真实输出
    yHat - 预测输出
Output:
    (bias**2).sum() - 损失值
"""
def loss(yTrue,yHat):
    bias = yTrue.flatten().A[0] - yHat
    return (bias**2).sum()
y01hat = caluc_yhat(test_arr=dataMat[0:99],dataMat=dataMat[0:99],yMat=labelMat[0:99],k=0.1)
y1hat = caluc_yhat(test_arr=dataMat[0:99],dataMat=dataMat[0:99],yMat=labelMat[0:99],k=1)
y10hat = caluc_yhat(test_arr=dataMat[0:99],dataMat=dataMat[0:99],yMat=labelMat[0:99],k=10)
loss01  = loss(yTrue=labelMat[0:99],yHat=y01hat)
loss1 = loss(yTrue=labelMat[0:99],yHat=y1hat)
loss10 = loss(yTrue=labelMat[0:99],yHat=y10hat)
print(loss01)
print(loss1)
print(loss10)
ay01hat = caluc_yhat(test_arr=dataMat[100:230],dataMat=dataMat[0:99],yMat=labelMat[0:99],k=0.1)
ay1hat = caluc_yhat(test_arr=dataMat[100:230],dataMat=dataMat[0:99],yMat=labelMat[0:99],k=1)
ay10hat = caluc_yhat(test_arr=dataMat[100:230],dataMat=dataMat[0:99],yMat=labelMat[0:99],k=10)
aloss01  = loss(yTrue=labelMat[100:230],yHat=ay01hat)
aloss1 = loss(yTrue=labelMat[100:230],yHat=ay1hat)
aloss10 = loss(yTrue=labelMat[100:230],yHat=ay10hat)
print(aloss01)
print(aloss1)
print(aloss10)

使用较小的核将在训练集上得到较低的误差。那么，为什么不在所有数据集上都使用最小的核呢？这是因为使用最小的核将造成过拟合，对新数据不一定能达到最好的预测效果。从上述结果可以看到，在上面的三个参数中，核大小等于10时的测试误差最小，但它在训练集上的误差却是最大的。

缩减系数来"理解"数据

岭回归

lasso

前向逐步回归

权衡偏差与方差

预测乐高玩具的价格