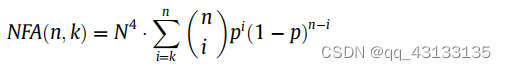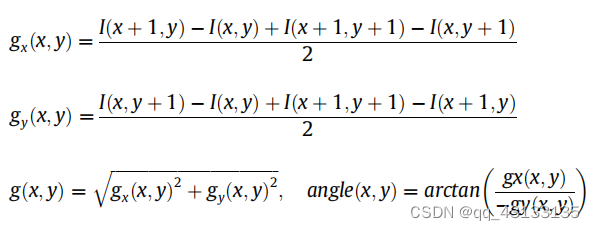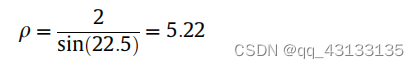摘要

我们提出了一种线性时间线段检测器，其结果准确，不需要参数调整，运行速度比文献中最快的线段检测器快11倍; 即Grompone von Gioi等人的线段检测器(LSD)。该算法利用了我们的新边缘检测器——边缘绘制(ED)算法产生的干净、连续(连通)的边缘像素链;因此得名EDLines。由于亥姆霍兹原理，检测器包括一个行验证步骤，该步骤允许它控制错误检测的数量。凭借其准确的结果和惊人的速度，EDLines将非常适合于下一代实时计算机视觉和图像处理应用。

简介

线段检测是图像处理和计算机视觉中一个重要而又反复出现的问题，有着广泛的应用。线段不仅对图像中的物体进行了高层次的描述，它们还有助于图像压缩(Franti等人，1998年)、材料中的裂纹检测(Mahadevan和Casasent, 2001年)、立体匹配(Ji和张，1988)，机器人导航(Kahn et al.， 1987, 1990)，路基检测(Tupin et al.， 1998)，运动视频和卫星图片的处理(Yu et al.， 2005)，以及许多其他(Zheng et al.， 2005;朱等，2001)。
理想的线段检测算法可以处理任何图像，无论其来源、方向或大小，并产生鲁棒和准确的线段，即在非常短的时间内，最好是实时的，没有错误检测。此外，这种算法根本不需要参数调优，对所有类型的图像只使用一组默认参数运行。本文提出的线段检测算法EDLines (Akinlar and Topal, 2011)满足了这些要求。
传统的线段检测算法从计算边缘图开始，典型的是著名的Canny边缘检测器(Canny, 1986)。下一步是应用霍夫变换(Hough, 1962;Illinworth和Kittler, 1988;Kalviainen等人，1996)，最后提取出包含一定数量边点的所有直线。使用间隙和长度阈值将线分割成段(Duda和Hart, 1972)。这些方法通常很慢，并且他们通常结合非连续线段产生很多错误的检测。
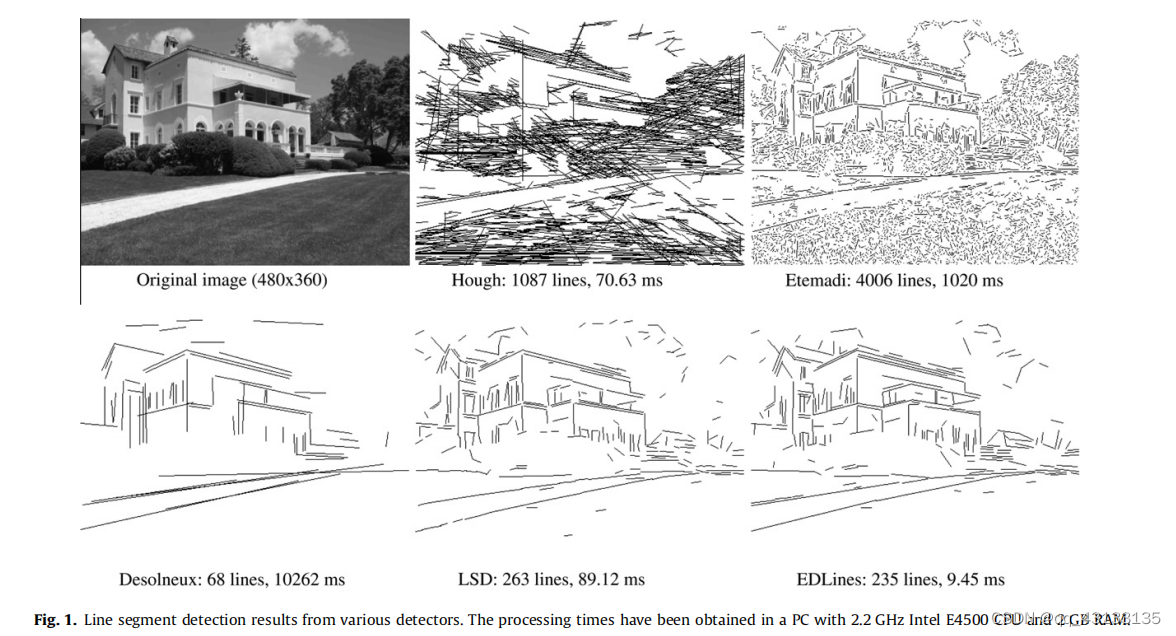
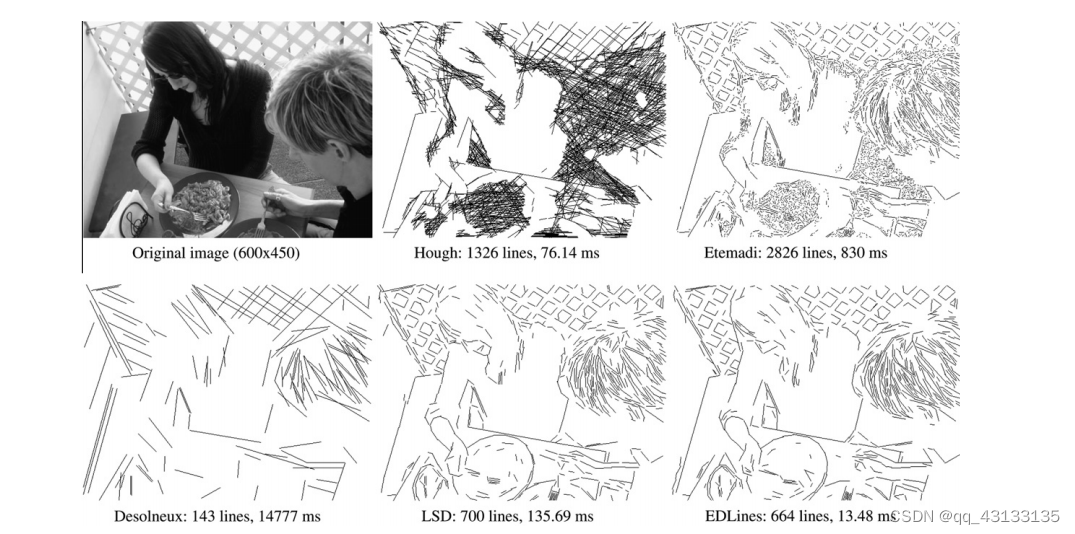
霍夫变换(Hough transform, HT)有很多变体，如随机霍夫变换(Xu et al.， 1990)，渐进概率霍夫变换(Kiryati et al.， 1991;Matas等人，2000;Galambos等人，2001)，椭圆高斯核的霍夫transform （Fernandes and Oliveira， 2008;KHT 软件包），等(Princen等人，1990;戈尔曼和克洛斯，1976年;Lam等人，1994;Kang等人，2007;Chao等人，2009)，每个尝试以弥补标准霍夫变换的不同缺点。在这些技术中，(Fernandes和Oliveira, 2008;KHT软件包)脱颖而出，为HT程序提出了一个有效的投票方案。给出一个二值边缘图，KHT在实现软件实时性的同时，对伪线检测具有较强的鲁棒性。KHT还有一组默认参数，可用于所有边缘映射。然而，所有基于霍夫变换的技术都需要一个二进制的边缘图作为输入，它们通常生成无限长的线——而不是线段——在(角度，半径)表示中，然后必须被分解成线段。对于这些技术来说，一个干净的输入边缘图是非常关键的，但是用于边缘图生成的参数不是自动的，必须由用户决定。图1是OpenCV的Hough变换方法即cvHoughLines2函数产生的线段。为了得到这一结果，在Canny边缘检测和线提取过程中通过试错设置不同的阈值，并给出了最佳的结果。虽然在房子上检测到的一些长线段是准确的，但有许多不相干的线段检测，特别是在各向异性结构周围，如灌木丛、草地和树木。KHT软件包生成的Hough变换结果虽然比OpenCV的cvHoughLines2快很多，但由于KHT生成的是无限长的直线而不是线段，需要通过后期处理步骤将线段分解成线段，所以本文没有给出Hough变换结果。记录中，KHT软件包只需要16.5 ms(生成Canny边缘图的时间为5 ms，提取线条的时间为11.5 ms)，输出360行。

Chan and Yip(1996)和Etemadi(1992)在计算边缘图后提出了不同的提取线段的技术，而不是使用Hough变换。具体来说，Etemadi的方法(Etemadi, 1992)是基于从给定的边缘地图生成像素链的思想，然后通过遍历这些链来提取线段和弧段。虽然线段和圆弧提取过程是无参数的，但边缘检测仍然需要留给用户的参数。该方法产生了局部化良好的线段和弧段，但其产生的线段太多，且存在大量的假阳性，特别是在背景有噪声或包含复杂结构(如树、草、多云天空或类似的各向异性结构)的图像中。图1显示的是仅显示线段的Etemadi结果。
除了使用二值边缘图进行线段检测外，还有一些技术只利用像素的梯度方向(Burns等人，1986;贝弗里奇et al.， 1996;Desolneux等人，2000,2008;来自Gioi的问候等人，2008a,b, 2010)。第一个这样的建议要归功于伯恩斯(1986)和Beveridge等人(1996)，他们计算了每个像素的线方向，然后通过组合具有相同方向的像素生成线段。从一个像素开始，它们观察相邻像素的水平线角度，如果它们有相同的方向，就将它们合并。虽然这项工作为最近的一些线路检测器奠定了基础，但它产生的结果与Etemadi的方法相似，产生了太多的线段和大量的误报。
solneux等人(2000,2008)采用了Burn利用像素方向的思想，提出了一种控制误报数量的无参数直线检测器。他们的想法是计算在某个方向上对齐的像素的数量，如果观察到的结构在感知上是有意义的，那么就接受这组像素作为线段。这被称为格式塔理论中的亥姆霍兹原理(solneux et al.， 2008)，并被用作线验证方法。虽然这种方法没有产生预期的假阳性结果，但许多有效的短线段缺失(见图1中solneux等人的结果)。该方法在本质上也是非常全局的，产生了非常长的线段，实际上应该被分解成几个更小的线段(观察两个不同楼层的窗户的侧面已经被合并)。此外，该算法的计算量非常大，因此非常慢(对给定的图像需要超过10秒的时间)。
通过扩展Burns的线段生成方法，并将其与solneux的线段验证方法相结合亥姆霍兹原理（Desolneux等人，2008），Grompone von Gioi等人(2008a,b, 2010)最近提出了一种无参数线段检测算法，称为线段检测器(LSD)，它可以产生精确的线段，还可以控制误检的数量。虽然LSD对于大多数类型的图像都有很好的效果(见图1 LSD的结果)，但是在背景中含有一些白噪声的图像中，LSD的效果很差，运行时间仍然很长;这使得它不适合新一代的实时应用。
在本文中，我们提出了一种快速、无参数线段检测器，名为EDLines (Akinlar和Topal, 2011)，产生稳健和准确的结果，运行速度比已知最快的线段检测器快11倍;即Grompone von Gioi等人的LSD (2008a,b, 2010)。由于Helmholtz原理(Desolneux et al.， 2008)，我们的探测器还包括一个行验证步骤，它让它控制误检的数量。从EDLines得到的结果可以看出，它和LSD的结果非常相似，检测到了所有的主要线段，假阳性也很少。此外，EDLines以惊人的9.45毫秒的速度实时运行，比给定图像的LSD快10倍。
EDLines由三个步骤组成:(1)给定一个灰度图像，我们首先运行我们的快速、新颖的边缘检测器，边缘绘制(ED)算法(Topal et al.， 2010;Topal和Akinlar，已提交出版;它生成一组干净的、连续的像素链，我们称之为边缘段。边缘段直观地对应于物体的边界。(2)接下来，我们利用直线度准则，即最小二乘直线拟合法，从生成的像素链中提取线段。 (3)最后，根据Helmholtz原理进行线验证步骤(Desolneux et al.， 2008;Grompone von Gioi等人，2008a)用于消除错误线段检测。
在第2节中，我们简要描述了我们的边缘检测器，边缘绘制(ED)算法(Topal et al.， 2010;Topal和Akinlar，已提交出版;边缘绘图网站)。第3节描述如何将线条与ED产生的像素链匹配。第4节描述线条验证步骤。第5节讨论了算法内部的默认参数，这些参数是固定的，对于不同的图像不会改变。第6节通过实验比较了EDLines与文献中其他EDLines的性能，第7节对本文进行了总结。

2. 边缘绘制边缘检测

边缘绘制(ED)是我们最近提出的新颖、快速的边缘检测算法(Topal等，2010;Topal和Akinlar，已提交出版;边缘绘图网站)。ED与现有边缘检测器(如Canny(1986))的区别在于:其他边缘检测器输出的是二值边缘图像，其中检测到的边缘像素通常是独立的、不相交的、不连续的实体;ED产生一组边缘片段，它们是干净的、连续的，也就是连接的边缘像素链。因此，虽然其他边缘检测器的输出需要进一步处理来生成潜在的物体边界，甚至可能不可能或导致不准确;ED不仅在默认情况下生成完美连接的对象边界，而且与其他边缘检测器相比，它还以惊人的速度实现了这一点(Topal等，2010)。
给定一幅灰度图像，ED分四个步骤进行边缘检测:

(1)首先对图像进行滤波，如高斯滤波，抑制噪声，使图像平滑。我们使用一个默认o = 1的5x5高斯核函数。(2)下一步计算平滑图像每个像素处的梯度大小和方向。任何已知的梯度算子，如Prewitt, Sobel, Scharr等，都可以在这一步使用。(3)在第三步中，我们计算一组像素，称为锚点(anchor)，这些像素是边缘元素(edgels)的概率非常高的像素。锚点对应于梯度运算产生最大值的像素，即梯度图的峰值。(4)最后，通过绘制锚点之间的边来连接第三步计算的锚点;因此命名为边缘绘制(ED)。整个过程类似于儿童边界完成拼图，给孩子一个物体的虚线边界，让他通过连接这些点来完成边界。ED从一个锚点(点)开始，利用相邻像素的梯度大小和方向，通过遍历梯度最大值走向下一个锚点。如果你把梯度图想象成一座3D的山，这很像从一个山顶走到另一个山顶。

图2显示了ED在128 x 128像素灰度图像上的作用。图2(b)为梯度图，白色像素对应高梯度值(山顶)。图2?显示了一组锚点示例，它们对应于梯度图的峰值，并清楚地描绘了图像中矩形的边界。如图2(d)所示，通过连接锚点(点)得到最终的边缘地图(ED如何连接锚点以获得最终边缘地图的详细描述，请参阅Topal等人(2010))。如前所述，ED不仅会产生类似于其他边缘检测器的二值边缘图，还会产生一组边缘段，这些边缘段是与物体边界相对应的像素链。在给定的例子中，ED生成了四个边段，一个为每个矩形的边界。给定这些边缘段，线段提取剩下的就是遍历这些像素链，并对像素进行虚线提取。下一节将介绍这是如何完成的。

3.线段提取

给定一个由连续的边缘像素链组成的边缘段，这一步的目标是将这条链分裂成一个或多个直线段。其基本思想是依次遍历像素点，使用最小二乘直线拟合方法将直线与像素点拟合，直到误差超过一定的阈值，如1像素误差。当误差超过这个阈值时，我们生成一个新的线段。然后，算法递归地处理链上的剩余像素，直到处理完所有像素。
表1显示了从像素链中提取线段的算法。其思想是通过最小二乘直线拟合方法生成一个最小长度的初始线段(第一个while循环)，然后通过添加更多像素来扩展这个线段(第二个while循环)。最小行长度的值取决于行验证参数，在章节5.4中解释。在检测出最小长度的初始线段后，我们只需遍历链上剩余的像素，计算每个像素到当前拟合直线的距离。只要像素距离当前行在一定距离内，我们就向当前行添加像素，例如1像素误差。直观地说，我们会继续向当前线段添加像素，直到出现一个转角，线段的方向发生变化。此时，我们输出当前线段。然后递归处理链的剩余像素以提取进一步的线段。

4. 直线验证

与Desolneux 等人.(2000)和LSD (Grompone von Gioi 等人， 2008b, 2010)相似，我们的线验证方法是基于Helmholtz原理，基本上说一个结构要感知有意义，这个结构(分组或格式塔)偶然的期望必须很低(Desolneux et al.， 2008)。

这是一种“反向”方法，将对象检测为背景模型的异常值。如solneux 等人(2000)所示，一个合适的背景模型是所有像素(即梯度角度)都是独立的。他们表明这种模型最简单的是高斯白噪声。为了使Helmholtz原理的验证更加具体，solneux对线段的“假报警数(NFA)”的定义如下(solneux 等人， 2000):设a为长度为“n”的线段，在大小为N × N像素的图像中，至少有“k”个点的方向与a的方向对齐。定义A的NFA为:

其中 $N^4$ 为Nx N幅图像中潜在线段的数量。这是因为一条线段有两个端点，每个端点可以位于图像的 $N^2$ 个像素点中的任何一个，因此总共有 $N^2 × N^2 =N^4$ 条线段。二项式尾计算中使用的概率“p”是直线方向的精度，其值将在第5节中讨论。
如果一个事件(这里是线段)的NFA(n, k) ≤ε，则称为ε-有意义的。solneux等人(2000)建议将ε设置为1，这对应于每个图像一次错误检测。给定这些定义，我们验证线段如下:对于长度为“n”的线段，我们计算线段上每个像素的梯度角度，并计算对齐像素的数量为“k”。然后我们计算NFA(n, k)，如果NFA(n, k)≤1，则接受线段有效。否则该行将被拒绝。需要指出的是，我们在验证步骤中按照“反向”框架的要求对原始的未滤波图像执行梯度计算。我们还需要注意的是，行验证是EDLines的最后一个可选步骤，如果认为不必要，可以省略。我们观察到，线条验证只拒绝较短的线段。长线条是对背景的大偏离，永远不会被拒绝。因此，一个只使用较长的行(如立体匹配)的应用程序，可以通过Helmholtz原理完全跳过行验证，并使用基于可以更快测试的原理的直线验证方法，例如，挑选超过某个阈值的行。这将进一步加快EDLines的速度。

5. 内部参数

EDLines使用了几个内部参数。下面，我们将描述这些参数，并解释如何以及为什么设置它们。

5.1. 梯度大小和方向计算

回顾第2节，我们的边缘绘制(ED)算法的第一步是计算图像的梯度。要计算像素(x, y)处的梯度大小和水平线角度，我们遵循Burns等人(1986)和Desolneux等人(2008)，以及LSD(Grompone von Gioi等人，2010;)，并使用2 × 2掩模，如下所示:

其中I(x, y)为输入图像在像素(x, y)处的强度，g(x, y)为梯度幅值，角(x, y)为水平线角。Grompone von Gioi等人(2010)的作者指出，使用这样一个简单的梯度算子的原因是为了减少计算梯度的依赖性，从而尽可能地保持像素独立性;因为，由于亥姆霍兹原理，“反向”验证需要像素独立性。

5.2. 直线验证参数

回顾第4节，我们的直线验证是基于线段的长度和直线上对齐的像素的数量。要应用这个定义，我们需要定义“对齐”的含义。我们借用了solneux等人(2000)的定义:两个点(或线段)P和Q具有相同的方向，即，如果角§和角(Q)之间的距离在t/n度内，则对齐精度为1/n。solneux还指出:“根据心理物理学和数值实验，‘n’不应该超过8”。Burns et al. （1986）和 LSD （Grompone von Gioi et al.，2010年)也得出了同样的结论。因此，我们假设两个点(即一个点和一条线段)的夹角在n/8 = 22.5°内对齐。这对应于8个不同的角度方向和精度“p=1/ 8= 0.125”。这是NFA计算中使用的概率。

5.3. 梯度阈值、锚阈值和扫描间隔

在ED中进行梯度计算后，锚点计算链接时忽略梯度值小于某一阈值“p”的像素。这可以让我们消除不包含边缘元素(边)的像素，因此没有线段。根据Grompone von Gioi et al.(2010)的讨论，我们设置“p”，以去掉角度误差大于角度公差的点。两个连续像素之间的最大量化误差等于2(相邻像素的误差为+1和-1时发生)，角度容差为22.5°(参见第5.2节)，我们通过Grompone von Gioi等人(2010)给出的以下公式计算梯度阈值:

浏览梯度图并消除梯度值小于“p”的像素，我们得到了我们所称的图像“边缘区域”。这些是边缘可能被定位的像素点。此外，所有被消除的像素都不可能包含边缘胶。
ED还有两个参数:锚定阈值和扫描间隔(在Topal等人(2010)中称为细节比率)。如第2节所述，在计算阈值梯度聚类，称为边缘区域(图2(b))后，ED计算一组锚(图2?)，这些锚使用智能路由过程进行链接，以获得最终的边缘段(图2(d)) (Topal et al.， 2010)。目前，ED通过带一个阈值的非最大抑制来执行锚计算，称为锚阈值。经典的非最大抑制算法认为，如果一个像素的梯度值大于或等于该像素在梯度方向上的两个相邻像素，则该像素为边缘候选像素;而ED算法则认为，如果一个像素的梯度值大于其在梯度方向上的两个相邻像素的锚定阈值，则该像素为锚定候选像素。设置锚点计算阈值的原因是为了选择优质的锚点，因为这将导致高质量的边缘段。锚阈值的最优取值没有理论依据;这个选择纯粹是经验之谈。因此，在EDLines中对多种不同类型的图像进行多次实验后，我们得出结论:锚定阈值为3的图像可以得到优质的边缘分割，因此线段质量也很好。ED的其他参数Scan Interval用于选择不同行/列间隔的锚点。这个参数的目的是调整锚点的数量，从而调整最终边缘地图的细节量。ED的扫描间隔为“k”，它扫描每k行/列的锚点。因此，Scan Interval为1表示ED扫描每一行/列，即每像素;Scan Interval为4表示ED每4行/列扫描一次。随着锚点数量的减少，最终边缘地图中的细节也会减少，反之亦然。由于我们想要检测给定图像中的所有线段，我们希望ED产生一个包含图像中所有细节的边缘地图;因此，我们在EDLines中将Scan Interval设置为1。

5.4. 直线适配的参数

一条像素链的直线拟合有两个参数:(1)最小直线长度(2)最大均方拟合误差。
回顾第4节，长度为“n”且对齐像素为“k”的线段在NFA(n, k) ≤1时有效。为了使最小长度的行有效，“k”必须等于“n”。因此，我们得到 $NFA(n, n) = n^4 *P^n ≤ 1$ 。由公式求出最小线长n，得到: $n≥\frac{-4log(N)}{log(P)}$ ，其中p= 0.125。作为一个日志（p）例如，对于512 x 512的图像，最小的行长度是12像素。最小线段长度是在拟合开始阶段使用该公式计算的，我们不检测线段短于最短有效线。最大均方拟合误差是EDLines拟合步长的另一个参数(算法见Table 1)。当我们扩展线段时，我们不断计算一个像素到当前拟合直线的距离。如果错误超过一定的阈值，我们输出当前线段，并开始一个新的线段。在我们的算法中，我们通过对不同图像集的多次实验，将该参数固定为1像素误差。

6. 实验

我们通过评估边缘绘制(ED)的边缘图及其对最终提取线段的影响来开始实验。
在这里插入图片描述

在所有EDLines实验中，首先使用o = 1的5x 5高斯核对图像进行平滑，EDLines运行时使用Section 5中描述的其他固定的内部参数。回顾5.3节，ED的梯度阈值(Gradient Threshold)是理论上计算的，而ED的锚定阈值(Anchor Threshold)是一个经验参数，需要通过实验来确定。图3展示了三幅图像，分别采用锚阈值1和3两种不同的ED边缘图，以及从这些边缘图中提取的线段。第一行显示高斯白噪声图像。根据亥姆霍兹原理，在这幅图像中不需要检测线段。从边图中我们可以看到，ED产生了大量类似垃圾的边段，这导致了很多短线段(图中没有显示);但在验证步骤中，所有提取的线段都被删除，线段检测为零。第二行是一座有树的房子。同样，ED的边缘图包含了许多树周围的垃圾形状，在验证步骤中几乎完全消除了。第三行显示一辆卡车在方格道路上行驶。EDLines似乎检测所有有意义的线段与两个边缘地图。还要注意EDLines对所有图像的实时行为。我们从第二幅和第三幅图像中观察到更多的线段被检测到，锚阈值为1。这是意料之中的，因为较小的锚定阈值将导致更多的锚定和更详细的边缘地图，但边缘地图只会在非常微小的细节上有所不同。两种边缘映射都指向相同的长线段;区别只存在于非常短的线段中。选择一个更大的锚阈值将进一步减少ED的边缘地图的细节，但这有错过一些重要的细节的风险，特别是在具有平滑过渡的边界。如果在这些边界上没有检测到锚点，就不会检测到边缘段;因此不会检测到线段。考虑到所有这些因素，我们在许多不同的图像集上的实验将ED的锚定阈值固定为3，并将在其余的实验中使用这个值.
我们现在将EDLines (EDLines Web站点)的性能与文献中的其他线条提取算法进行比较。图4为样本挑战性图像的不同检测器线段提取结果。已获取在2.2 GHz Intel E4500 CPU和2gb RAM的PC机上的处理时间。
为了得到Hough变换的结果，我们首先使用OpenCV中的cvCanny函数，将低阈值设为40，高阈值设为100，生成一个二值边缘图。然后我们将得到的边缘映射送入cvHoughLines2函数，将Hough方法设置为CV_HOUGH_PROBABILISTIC，线累加器阈值为40，最小线长阈值为10。通过试错确定边缘检测和直线拟合的阈值，以获得最佳的感知结果。从结果中，我们看到有一些准确的线段检测，但也有很多不相关的线段检测，特别是在各向异性结构，如地毯，头发和意大利面。我们还应该注意到OpenCV的概率Hough变换的实现是惊人的快。
为了得到Etemadi的结果，我们使用cvCanny得到的相同的边缘图，并将其输入到ORT-2.3软件包中实现的Etemadi原始的线和弧提取算法中。这里只显示检测到的线段。从结果来看，我们看到Etemadi的方法产生了太多的线段，有很多假阳性，特别是在图像的各向异性部分(类似于霍夫变换)，需要相当长的时间来执行。
为了获得solneux等人的结果，我们使用了自由分布的图像处理框架MegaWave2中包含的falign_mdl实用程序)。因为这个方法是无参数的，所以我们使用默认参数运行它。从结果来看，我们看到，荒芜等人的方法没有承诺的假阳性。但它忽略了一些有效的短线段，它在本质上是非常全局的产生非常长的线段实际上应该被分解成几个更小的线段。此外,这种方法对样本图像进行14 s以上的处理，计算量非常大。

为了获得LSD产生的结果，我们从IPOL (LSD)下载了免费分发的LSD包。因为LSD是无参数的，所以我们使用默认参数运行它。我们必须注意到，在默认情况下，LSD将图像的宽度和高度缩放了0.8;也就是说，它将原始图像缩小到处理前的64%。本文给出的LSD结果是基于0.8尺度参数的。由于没有任何伸缩性，LSD需要更长的时间来执行，并产生更多(特别是短)线段。查看结果，我们看到LSD产生了很好的结果，假阳性很少，但它的运行时间仍然令人望而却步，特别是对于实时应用程序。此外，如Grompone von Gioi等人(2010)所指出的，LSD在含有白噪声的图像中开始失效，如下图所示。
图4的最后是EDLines生成的结果。从结果可以看出，它与LSD的检测结果非常相似，主要线段都检测到了，假阳性也很少。然而，与LSD不同的是，EDLines以13.48毫秒的惊人速度实时运行，对于给定的样本图像，大约比LSD快10倍。
图5显示了EDLines对几幅自然图像产生的结果。左边一栏的图像具有几何结构，如正方形、矩形和其他多边形;右边这一栏的图像是非几何结构。看，EDLines在每一种情况下提取图像的结构，假阳性很少。弯曲的物体，如人类的头或自行车车轮，已经被一些线段串联起来近似。
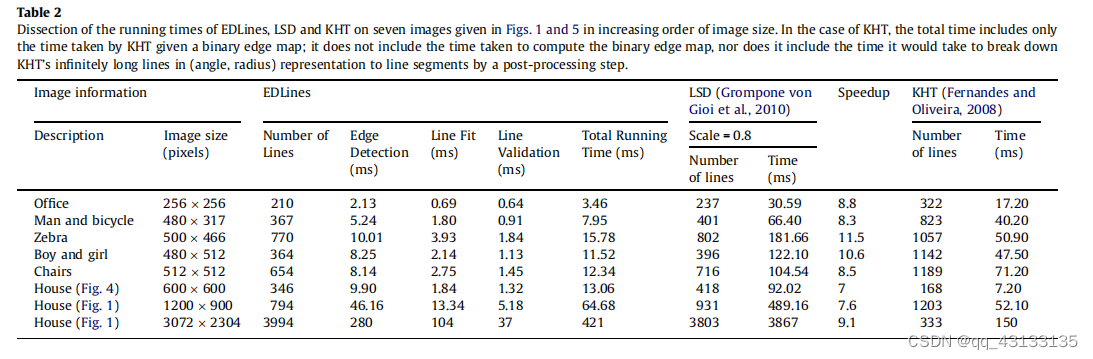
Table 2展示了EDLines运行时间的解剖，LSD (Grompone von Gioi et al.， 2010)和KHT (Fernandes and Oliveira, 2008)在图1和图5所示的7张图像上按图像大小的递增顺序进行。在KHT的情况下，总时间只包括给定二元边映射的KHT所花费的时间;它不包括计算二进制边缘映射的时间，也不包括通过后处理步骤将KHT无限长的线(角度，半径)表示分解为线段所需的时间。我们看到EDLines和LSD在每种情况下产生的结果非常相似，但EDLines的运行速度至少比LSD快7倍，最多11倍。我们还看到EDLines大约65%的运行时间花费在边缘段链的生成上。直线拟合大约占总运行时间的25%，直线验证占总运行时间的剩余10%。如前所述，行验证是EDLines中的一个可选步骤，如果认为不必要，可以省略。例如，在立体匹配应用程序中，通常会使用较长的行，因此可以使用基于行长度的简单行验证方案。由于在验证步骤中不会拒绝长行，所以这样一个简单的验证方案是可行的。这将进一步加快EDLines的速度。

图6展示了白噪声对不同算法线段检测的影响。在本次实验中，我们取图1中的house图像，加入一些高斯白噪声，并将其输入到各种探测器中。图6中的三行分别对应全分辨率、半分辨率和四分之一分辨率的分析。在全分辨率下，Hough和Etemadi会产生无用的结果，而LSD则无法检测到图像的总体结构。在一半和四分之一的分辨率下，霍夫、埃特马迪和LSD的情况开始好转。然而，EDLines提取了图像的一般结构Atlall分辨率只有少数假阳性。LSD在完全分辨率下失败的原因是噪声的存在阻止了线支持区域的增长，因此只形成了小的线段。这些小片段随后在验证步骤中被消除，因此只进行了少量检测(Grompone von Gioi等人，2010)。然而，EDLines在所有分辨率下提取图像的一般结构，只有少数假阳性。LSD在完全分辨率下失败的原因是噪声的存在阻止了线支持区域的增长，因此只形成了小的线段。这些小片段随后在验证步骤中被消除，因此只进行了少量检测(Grompone von Gioi等人，2010)。然而，EDLines能够在所有分辨率下检测图像的一般结构。
为了更好地分析噪声对EDLines的影响，我们用三幅噪声合成图像进行了另一个实验。结果如图7所示。图7第一行图像有一个添加了低水平高斯白噪声的垂直条带。噪声的存在使LSD无法在完全分辨率下探测到整个垂直线;相反，只检测到线路的某些部分。这是意料之中的，因为LSD中噪声的存在会影响线支持区域增长算法，所以只能形成较短的线支持区域。噪声也会增加这些支持区域的NFA值，因此在验证过程中，许多支持区域会被消除，只留下一些短线段(Grompone von Gioi等人，2010)。LSD提出的解决方案是进行多尺度分析，在更粗的尺度上处理图像。对同一幅图像进行半分辨率的分析表明，LSD现在能够检测到整个垂直线。至于EDLines，我们看到EDLines能够以全分辨率和半分辨率检测整行。这是由于ED的边缘检测使用了一个初始高斯平滑步骤，这显然足以处理可用的噪声。还要注意，ISD和EDLines都不会产生任何错误检测。

图7的第二行显示了相同的垂直条带，但添加了高水平的高斯白噪声。请注意，在高水平噪声的情况下，LSD无法在完全分辨率下检测任何线段。但在半分辨率下，LSD产生的结果还算合理。虽然整个垂直条带被检测为几个线段，但大多数垂直线似乎被检测到。EDLines也不能在完全分辨率下将整个垂直条带检测为一条线段。这一点。是由于以下原因:当噪声太强，ED默认的5 x 5高斯平滑核核(o =1)无法处理时，沿垂直条带的像素会有异常的梯度大小和方向。由于ED是通过连接锚来工作的，它利用了梯度值和方向(Topal等，2010)，垂直条带顶部的噪声像素会将ED转向噪声区域。这将使ED检测到的垂直条带不是单个边缘段，而是多个不相交的边缘段。因此，垂直条带将被检测为几个短线段，其中一些甚至可能在验证过程中被消除。这正是我们在给定的例子中所观察到的:EDLines将垂直条带检测为4个线段。但是请注意，在半分辨率下，EDLines能够将整个垂直条带检测为一个线段。这是因为通过高斯采样产生半分辨率图像是一个去噪步骤，足以处理添加的噪声。这就是为什么LSD和EDLines都能很容易地检测到垂直线。还要注意，LSD和EDLines都不会产生任何错误检测。
最后，图7中的第三行显示了一个模糊的垂直条带，添加了一些高斯白噪声。LSD同样无法在全分辨率下检测到任何线段，但可以在半分辨率下将整个垂直条带作为一条线段进行检测。EDLines也在半分辨率下将整个垂直条带作为一条线段检测，但在全分辨率下产生一些有问题的结果;尽管EDLines的检测都不能被归类为错误检测。EDLines能在全分辨率下观察到行为的原因可以归结为ED的边缘段检测策略: 在模糊的垂直条带周围，梯度大小和方向值变化非常快。这意味着，在锚连接过程中，ED不能沿着直线行走(就像它在非模糊的垂直带中一样)，而是在锚连接过程中所走的路径由几个弯曲的边缘段组成。当我们从这些歪边线段中提取线段时，我们得到的结果如图7所示。我们再次指出，EDLines在全分辨率下的检测不能被归类为错误检测，因为它们都落在模糊的垂直条带上。
通过以上实验我们可以得出结论，ED默认的去噪滤波器，即5 x 5高斯核，o = 1，不能处理所有类型和功率的噪声。这显然是意料之中的;但根据我们的经验，对于许多类型的自然图像，这种滤波器可以让ED产生高质量的边缘段，EDLines可以从中提取高质量的线段。在存在高功率噪声的情况下，EDLines始终可以利用类似于LSD的多尺度分析(Grompone von Gioi等人.， 2010)，并产生良好的结果，如图6和图7所示。

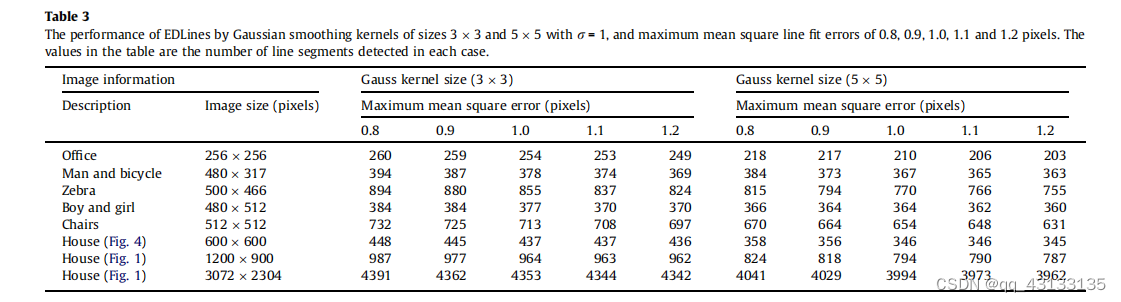
Table 3显示了高斯平滑和最大均方线拟合误差对EDLines性能的影响。表中的每个槽显示了给定参数集检测到的边缘段总数。回顾第2节和5.4节，EDLines默认使用5 x 5高斯平滑核，核值为1，最大均方线拟合误差为1像素。人们期望更多的高斯平滑和更大的线拟合误差会导致更少的线段。从表中的结果可以清楚地观察到这一点。还可以注意到，默认参数的变化不会对所获得的结果产生很大的变化，这是可取的。EDLines运行时性能的变化可以忽略不计，在表中没有显示。

7. 结论

EDLines是一种基于亥姆霍兹原理的具有误检控制的实时线段检测器。它是基于我们的新型边缘检测器——边缘绘制(ED)产生的边缘段链。本文中所展示的实验(以及读者可能希望在线执行的其他实验(EDLines Web站点))表明，EDLines产生了准确的、本地化良好的线段，只有少数误报，而且它以惊人的速度实现了这一点。由于EDLines是通过分析连续的像素链来工作的，因此它可以扩展到检测其他几何结构，如弧线、圆、多边形等，这是以后的工作。