[人工智能]周志华《机器学习》对率回归详细推导（包含习题）

1. 题目：

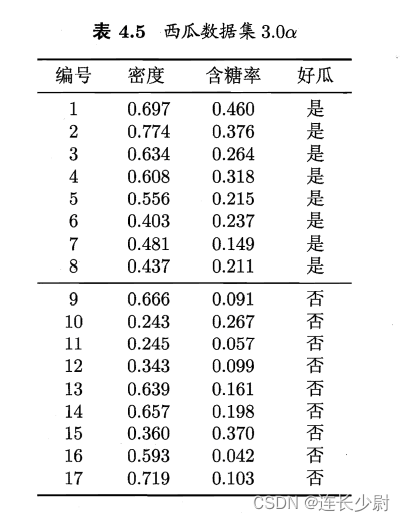
编程实现对率回归，并给出西瓜数据集3.0α上的结果。

数据集3.0α如下图

2. 对率回归（或逻辑回归）模型简介：

首先回顾线性回归模型：
$$y={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$
该模型训练后，最终会找到y与x之间的线性关系。但有些数据并不符合这种线性关系，而是符合g(y)与x是线性关系，这样对数据的要求就降低了，所以衍生出了广义线性回归模型：
$$y=g^{?1}({\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b)$$
而上述模型用于回归任务，如果考虑分类任务，我们则要将y看成是样本是正例的可能性，所以要保证预测值最终在0-1之间，所以我们需要将y外面套上一个对数几率函数：
$$g(x)=\ln \frac{x}{1?x}$$
将对数几率函数带入到广义线性回归模型，即可得到对率回归模型：
$$\ln \frac{y}{1?y}={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$
也可写成
$$y=\frac{1}{1+e^{?({\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b)}}$$

3.如何训练（对率回归推导）

首先，我们需要将y看成是正例的几率，写成p(y=1|x),
1-y看成是反例的几率，写成p(y=0|x)。带入到对率回归模型（上面那个）当中可以得：
$$\ln \frac{p(y=1|x)}{p(y=0|x)}={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$
现在求p(y=1|x)：
$$\ln \frac{p(y=1|x)}{1?p(y=1|x)}={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$
$$\frac{p(y=1|x)}{1?p(y=1|x)}=e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}$$
$$\frac{1}{1?p(y=1|x)}?1=e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}$$
$$p(y=1|x)=\frac{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}}{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}+1}$$
求p(y=0|x):
$$p(y=0|x)=1?p(y=1|x)$$
$$p(y=0|x)=\frac{1}{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}+1}$$
至此，得到了正例反例的概率分布，现在需要做的就是将w和b估计出来，这里就需要用到概率论与数理统计的参数估计知识中的极大似然法。极大似然法适用于分布已知，参数未知的情况，所以这里符合条件。极大似然法要求先找到“对数似然方程”l(w,b)，流程就是先将每个样本对应的概率得到，然后相乘，再取对数，就可找到对数似然方程，然后找到该函数得极大值点，对应就是w和b得估计值。回到本问题，首先得到对数似然为：
$$\mathbf{l}(\mathbf{w},b)=\sum _{i=1}^m\ln p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)$$
然后，在西瓜书中，为方便，规定了符号：
$$\mathbf{\beta }=(\mathbf{w};b)$$
$$\mathbf{x}=(\mathbf{x};1)$$
$$p_1(\mathbf{x};\mathbf{\beta })=p(y=1|\mathbf{x};\mathbf{\beta })$$
$$p_0(\mathbf{x};\mathbf{\beta })=p(y=0|\mathbf{x};\mathbf{\beta })$$
则可以对似然项进行重写：
$$p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=y_i{p}_1({\mathbf{x}}_{\mathbf{i}};\mathbf{\beta })+(y_i?1)p_0({\mathbf{x}}_{\mathbf{i}};\mathbf{\beta })$$
可以看到，在训练过程中，y只会取0和1，在y=1时，只有前一项有效，y=0时，只有后一项有效。
然后，对
$$p(y=1|x)=\frac{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}}{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}+1}$$
和
$$p(y=0|x)=\frac{1}{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}+1}$$
进行重写得：
$$p_1(\mathbf{x};\mathbf{\beta })=\frac{e^{{\beta }^{T}x}}{e^{{\beta }^{T}x}+1}$$
和
$$p_0(\mathbf{x};\mathbf{\beta })=\frac{1}{e^{{\beta }^{T}x}+1}$$
然后，将这两个式子带入到似然项中：
$$p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=y_i\frac{e^{{\beta }^T{x}_i}}{e^{{\beta }^T{x}_i}+1}+(1?y_i)\frac{1}{e^{{\beta }^T{x}_i}+1}$$
两边取ln，得
$$\ln p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=\ln [y_i\frac{e^{{\beta }^T{x}_i}}{e^{{\beta }^T{x}_i}+1}+(1?y_i)\frac{1}{e^{{\beta }^T{x}_i}+1}]$$
当yi = 1时：
$$\ln p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=\ln \frac{e^{{\beta }^T{x}_i}}{e^{{\beta }^T{x}_i}+1}={\beta }^T{x}_i?\ln (e^{{\beta }^T{x}_i}+1)$$
当yi = 0时：
$$\ln p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=\ln \frac{1}{e^{{\beta }^T{x}_i}+1}=?\ln (e^{{\beta }^T{x}_i}+1)$$
结合两个情况，可以看到，区别在于${\beta }^T{x}_i$项，所以可以在该项前面加上yi，得到最终为：
$$\ln p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)=y_i{\beta }^T{x}_i?\ln (e^{{\beta }^T{x}_i}+1)$$
可以看到，当yi=1时，第一项有效，当yi=0时，第一项无效。

然后，我们将上述推导的$\ln p(y_i|{\mathbf{x}}_{\mathbf{i}};\mathbf{w},b)$放回对数似然方程中（为看方便，截个图放这儿）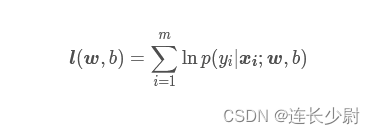
可以得到：
$$\mathbf{l}(\mathbf{\beta })=\sum _{i=1}^m[y_i{\beta }^T{x}_i?\ln (e^{{\beta }^T{x}_i}+1)]$$
现在，我们完成了对数似然方程的构造，按照极大似然法的流程，接下来只需要最大化“对数似然”$\mathbf{l}(\mathbf{\beta })$，就可得到w和b的估计值。但是，出于对机器学习中一般习惯于“最小化”（例如最小化损失函数），所以这里我们将$\mathbf{l}(\mathbf{\beta })$取个相反数得到$\mathbf{l}{}^{\prime }(\mathbf{\beta })$：
$$\mathbf{l}{}^{\prime }(\mathbf{\beta })=\sum _{i=1}^m[?y_i{\beta }^T{x}_i+\ln (e^{{\beta }^T{x}_i}+1)]$$
那么最大化$\mathbf{l}(\mathbf{\beta })$其实就等同于最小化$\mathbf{l}{}^{\prime }(\mathbf{\beta })$。
至此，就可以使用梯度下降法，找到$\mathbf{l}{}^{\prime }(\mathbf{\beta })$的极小点。对其梯度下降法总结起来就是一个公式：
$${\mathbf{\beta }}^{t+1}={\mathbf{\beta }}^t?s\frac{?\mathbf{l}{}^{\prime }(\mathbf{\beta })}{?\mathbf{\beta }}$$
其中$\frac{?\mathbf{l}{}^{\prime }(\mathbf{\beta })}{?\mathbf{\beta }}$为：
$$\frac{?\mathbf{l}{}^{\prime }(\mathbf{\beta })}{?\mathbf{\beta }}=?\sum _{i=1}^m{\mathbf{x}}_{\mathbf{i}}(y_i?p_1({\mathbf{x}}_{\mathbf{i}};\mathbf{\beta }))$$
s是步长，$\frac{?\mathbf{l}{}^{\prime }(\mathbf{\beta })}{?\mathbf{\beta }}$为梯度，每次下降按照梯度方向移动s单位，就可逐渐靠近极小点。找到极小点后，对应的$\beta$就是训练结果。

4.代码实现（python）

import numpy as np
import openpyxl
import matplotlib.pyplot as plt
from matplotlib import cm

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
    
def init_xy():
    sheet1 = openpyxl.load_workbook('./xigua3.0.xlsx')['Sheet1']
    x = np.zeros((2,17))
    y = np.zeros((1,17))
    for i in range(17):
        x[0][i] = sheet1[chr(ord('A')+i)+'1'].value
    for i in range(17):
        x[1][i] = sheet1[chr(ord('A')+i)+'2'].value
    for i in range(17):
        y[0][i] = sheet1[chr(ord('A')+i)+'3'].value
    return x.T, y.T
    
def function_p1(x_hat, b):
    a = np.math.exp(np.dot(np.transpose(b), x_hat))
    return a / (1+a)
    
def function_p2(x, b):
    return 1 - function_p1(x, b)

def train():
    x,y = init_xy()
    b = np.ones((3,1))
    dl_sub = 0
    train_n = 2000
    step_size = 0.1
    
    for step in range(train_n):
        dl = 0
        for i in range(17):
            x_t = x[i]
            x_hat = np.append(x_t, 1)
            x_hat = x_hat.reshape(3,1)
            dl_sub = np.dot(x_hat, y[i][0] - function_p1(x_hat, b))
            dl += dl_sub
        b = b + step_size * dl
    return b

def test(x, y, b):
    right = 0
    for i in range(17):  
        x_hat = np.append(x[i], 1)
        y_pre = sigmoid(np.dot(b.T, x_hat))
        if (y_pre >= 0.5 and y[i] == 1) or (y_pre < 0.5 and y[i] == 0):
            right += 1
            
    print("正确率为:", right/17)

b = train()
x,y = init_xy()
test(x, y, b)

5.运行结果