文章目录
MLP、CNN、RNN后的第四大模型。
Abstract
序列转录模型主要是采用RNN或者CNN。里面常常包含一种编码器和解码器的结构。
仅仅依赖于注意力机制。
该篇文章主要是针对机器翻译做的。后来应用在了不同的领域。
Introduction
问题:
- RNN是一个一步步计算的过程,无法并行,计算性能很差;
- 时序信息会随着序列的移动而丢失。
注意力机制很早就和RNN有所结合,更好地实现了编解码器之间的数据交互。
但是本文舍弃了RNN的结构,完全采用注意力机制来完成。
Background
用卷积神经网络对比较长的序列难以建模,需要用很多层卷积扩大感受野。卷积的优势在于有多个输出通道,每个通道可以学一个模式。
因此,本文提出了多头的注意力模型。
Model Architecture
对于序列模型来说,编码器-解码器结构在序列任务中有不错的表现。
对于解码器而言,在循环神经网络中,词是一个个输出的,过去时刻的输出会作为当前时刻的输入,这称为自回归。
对于解码器而言,是可以看到全部的句子的。编码器得到的序列整个交付给解码器。
Encoder and Decoder Stacks
Encoder:包含了六个堆积的模块,每个模块有两个子层。每一个模块中,两个子层都有相应的残差连接,随后经过标准化(LayerNorm)。
为了避免残差连接时,通道大小的不一致(需要做投影),本文将其的维度统一设置为512。
BatchNorm与LayerNorm
Internal Covariate Shift:训练的过程中,数据的分布在不断地变化,为下一层网络的学习带来了困难。
在训练的时候,对于一个二维矩阵,行代表样本,列代表特征,BatchNorm是将每列做一个标准化(算均值、标准差,Z-score)。在测试的时候,
通常而言,最后会用可学习的参数 γ , β \gamma,\beta γ,β,对得到的标准化的结果做一个线性变换,相当于是改变了这个分布的均值和方差。
这是因为,如果全都统一成标准正态分布,那模型学习到的特征分布就完全被消除了。因此有必要给他微调的机会。
我认为BN层起到的作用应该是一方面限制其分布不要太离谱,有一个基本的雏形,另一方面又不希望都是一个模子里刻出来的。
在测试时,用到的均值和方差的参数是在训练的时候算出来的。
公式为 μ = m μ + ( 1 ? m ) μ b a t c h , σ 同 理 \mu = m\mu+(1-m)\mu_{batch},\sigma同理 μ=mμ+(1?m)μbatch?,σ同理。
如果输入的是[B,C,H,W]的话,输出的是[C,H,W]。

LayerNorm是针对一个Batch中的一个Sample而言的。其计算的是所有channel中的每一个参数的均值和方差,进行归一化,即只在C维度上进行。
公式为 y = x ? E [ x ] V a r [ x ] + ? ? γ + β y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}\cdot\gamma+\beta y=Var[x]+??x?E[x]??γ+β
LN通常用在NLP中,因为NLP中一个Sample是一个句子,句子中的每一维度都是一个词,因此同一维度的词之间没有共性的特征关系,同时为了做BN还要padding没用的块,所以BN的效果很糟糕。
因此训练过程中归一化的对象是一个词。
因为是对每个样本自己来做的,所以没必要在训练过程中算全局的均值和方差。
Decoder:带掩码。使得训练和预测时的行为保持一致。其输入是Encoder的全部输出。
Attention
注意力函数一个query和一系列key映射成一个输出的函数。
Scaled Dot-Product Attention
常见的注意力机制有两种,分别是加法和点积。这里采用了点积的形式,因为其算起来比较高效。
但是这里还除了一个 d k \sqrt{d_k} dk??,目的是为了避免softmax这样的函数在训练过程中出现饱和的情况(最后出现当然是好的)。
这也是该注意力命名的由来。
接下来讲一下注意力函数 A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dk??QKT?)V
其中Q、K、V的每一个shape都是 ( n u m _ s a m p l e , n u m _ f e a t u r e ) (num\_sample,num\_feature) (num_sample,num_feature),可想而知, Q K T QK^T QKT的元素 ( i , j ) (i,j) (i,j)的含义是,我的第i个样本需要对第j个样本注意多少。
key,value的shape应该是一致的,query的shape可以和他们不一样。

怎么样做mask?
解码器中,是不能看到后续的内容的,所以让第t个时间的query只看前面的key。这里算还是正常算,就是最后将乘出来的结果t+1之后的数据变成一个很大的负数即可,softmax后就会变为0.
Muti-Head Attention

模拟多个输出通道,将输入的内容分割成很多个等大小的通道。

Applications of Attention in our Model
有三种不同的注意力层。
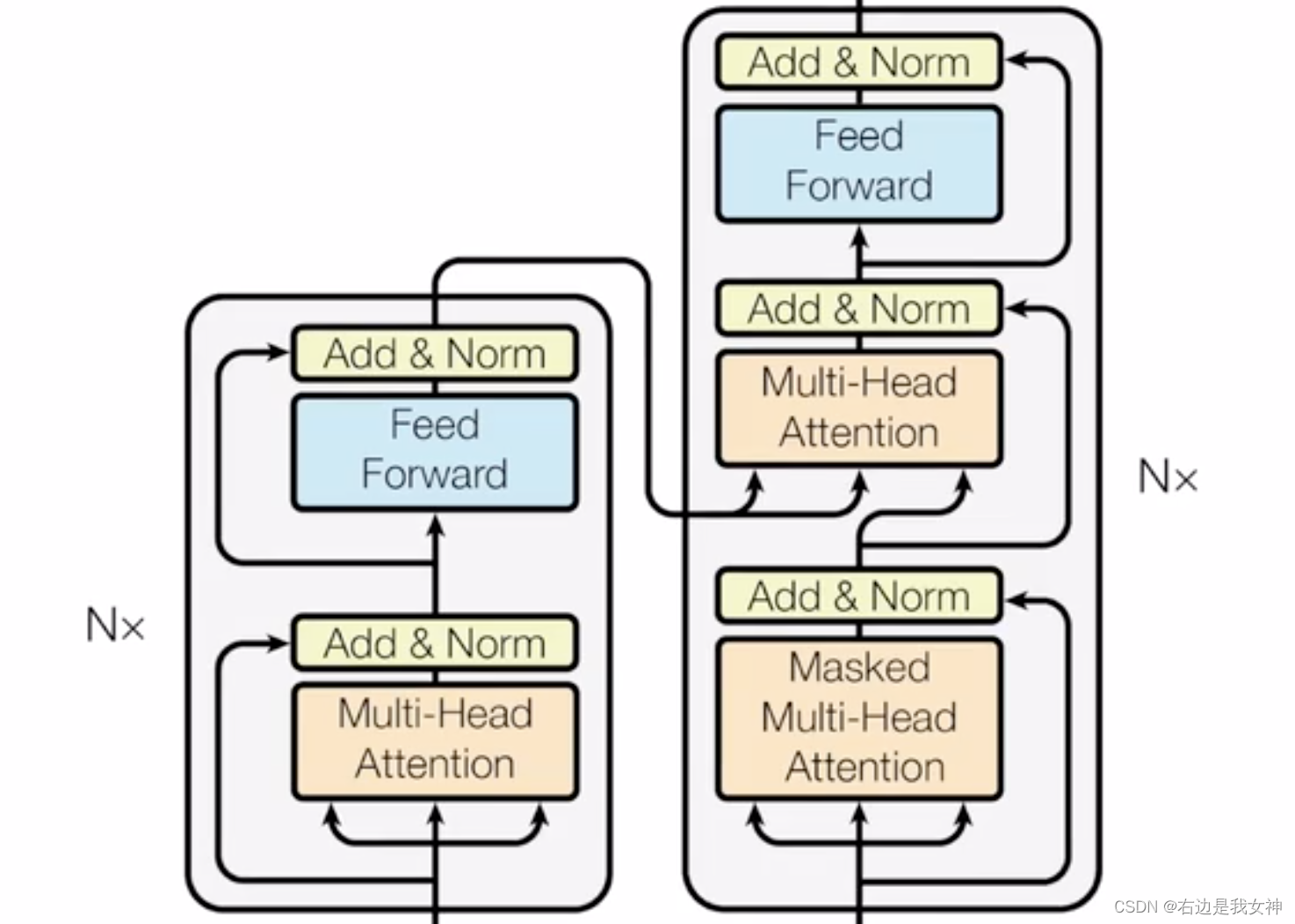
解码器的第一个注意力层有一个Mask的东西。
解码器的第二个注意力层的输入:key和value来自于编码器,query来自于上一个注意力层。
Position-wise Feed-Fordward Networks
说白了就是一个MLP,作用在最后一层。
单隐藏层MLP,中间的隐藏层将维度变成2048,之后再变回来。
公式为:
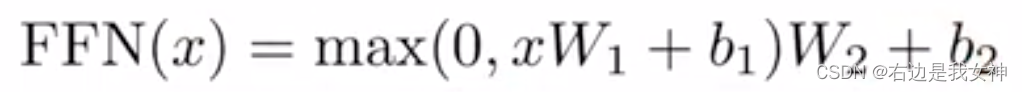
pytorch输入的是3d的话,默认是在最后一个维度做计算。
Attention起的作用的是将序列中的信息抓取出来,做一次汇聚。MLP的作用是映射成我想要的语义空间,因为每一个词都有了完整的序列信息,所以MLP是可以单独做的。
RNN也用MLP做一个转换,为了保证序列信息的获取,将上一时刻的输出输入到下一时刻的MLP。
Embedding and Softmax
就是将词映射成向量。
Positional Encoding
Attention是没有时序信息的,所以要进行位置编码。
P
(
p
o
s
,
2
i
)
=
sin
?
p
o
s
1000
0
2
i
d
m
o
d
e
l
P(pos,2i)=\sin \frac{pos}{10000^{\frac{2i}{d_{model}}}}
P(pos,2i)=sin10000dmodel?2i?pos?
P
(
p
o
s
,
2
i
+
1
)
=
cos
?
p
o
s
1000
0
2
i
d
m
o
d
e
l
P(pos,2i+1)=\cos \frac{pos}{10000^{\frac{2i}{d_{model}}}}
P(pos,2i+1)=cos10000dmodel?2i?pos?
Why Self-Attention

第一个比较的是计算复杂度、第二个是序列事件(并行性的度量)、第三个是最大路径长度(从序列的第一个位置到最后一个位置要走多久,体现信息的糅合性)。
Q K^T的话,n个样本和n个样本相乘,每次乘d次,所以是这个复杂度。
循环神经网络的话,进来一个d维度的样本,MLP进行对每一维度进行d次运算,共进行n次,所以是这个数。
目前来看的话两者的计算复杂度没啥区别。主要是后续的内容:Attention信息不容易丢失且并行度较高。
但是Attention对于模型的约束更少需要更大的模型和更多的约束才能训练出来。
Conclusion
使用了encoder-decoder的结构,不过将其中的recurrent layers换成了multi-headed self-attention。