目标检测 YOLOv5网络v6.0版本总结
YOLOv5对比YOLOv4
- 输入端:在模型训练阶段,提出了Mosaic数据增强、自适应锚框计算、自适应图片缩放等;
- Backbone网络:融合其它检测算法的新思路,主要有:Focus结构与CSP结构;
- Neck网络:YOLOv5在BackBone与最后的Head输出层之间往往会插入了FPN+PAN结构
- Head输出层:输出层的锚框机制与YOLOv4相同,主要改进了训练时的损失函数GIOU_Loss和预测框筛选的CIOU_nms
网络结构
-
YOLOv5s_5.x

-
YOLOv5s_6.x

与YOLOv5_5.x相比较,YOLOv5_6.x网络结构更加精简:
- Conv(k=6, s=2, p=2)替换Focus模块,便于导出其他框架
- SPPF模块替代SPP,并且将SPPF放在backbone最后一层
- backbone中的C3层重复次数从9次减小到6次
- backbone中最后一个C3层引入了shortcut(C3 n=1 True)
从结构图可以看出网络分为输入端、Backbone、Neck、Head输出端四个部分。YOLOv5包含:YOLOv5s、YOLOv5m、YOLOv5l、YOLOv5x四种版本,下面以YOLOv5s为例**:**
- 输入端:输入图像的大小为608*608,该阶段通常包含一个图像预处理阶段,即将输入图像缩放到网络的输入大小,并进行归一化等操作。在网络训练阶段,YOLOv5使用**
Mosaic数据增强操作提升模型的训练速度和网络的精度;并提出了一种自适应锚框计算与自适应图片缩放**方法。 - Backbone网络:
Backbone网络通常是一些性能优异的分类器网络,该模块用来提取一些通用的特征表示。YOLOv5中不仅使用了**CSPDarknet53结构**,而且使用了Focus结构作为基准。 - Neck网络:Neck网络通常位于
Backbone网络和Head网络的中间位置,利用它可以进一步提升特征的多样性及鲁棒性。YOLOv5 v6_x用SPPF替换掉了YOLOv5 v5_x的SPP,在计算结果相同的情况下SPPF计算速度比SPP快了两倍。在PAN结构中引入了CSP结构 - Head输出端:
Head用来完成目标检测结果的输出。针对不同的检测算法,输出端的分支个数不尽相同,通常包含一个分类分支和一个回归分支。YOLOv4利用GIOU_Loss来代替Smooth L1 Loss函数,从而进一步提升算法的检测精度。
输入端
-
数据增强
Mosaic
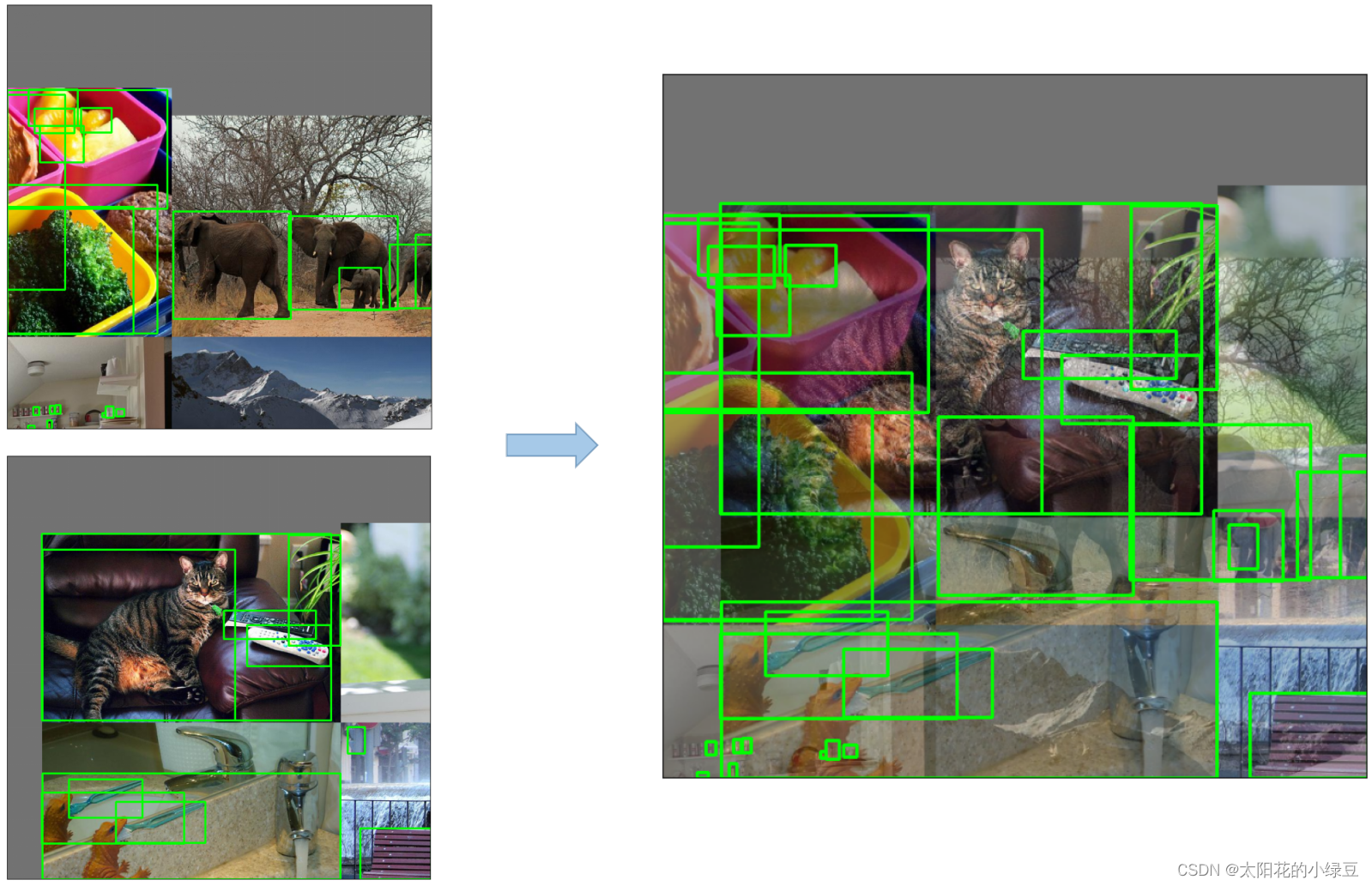
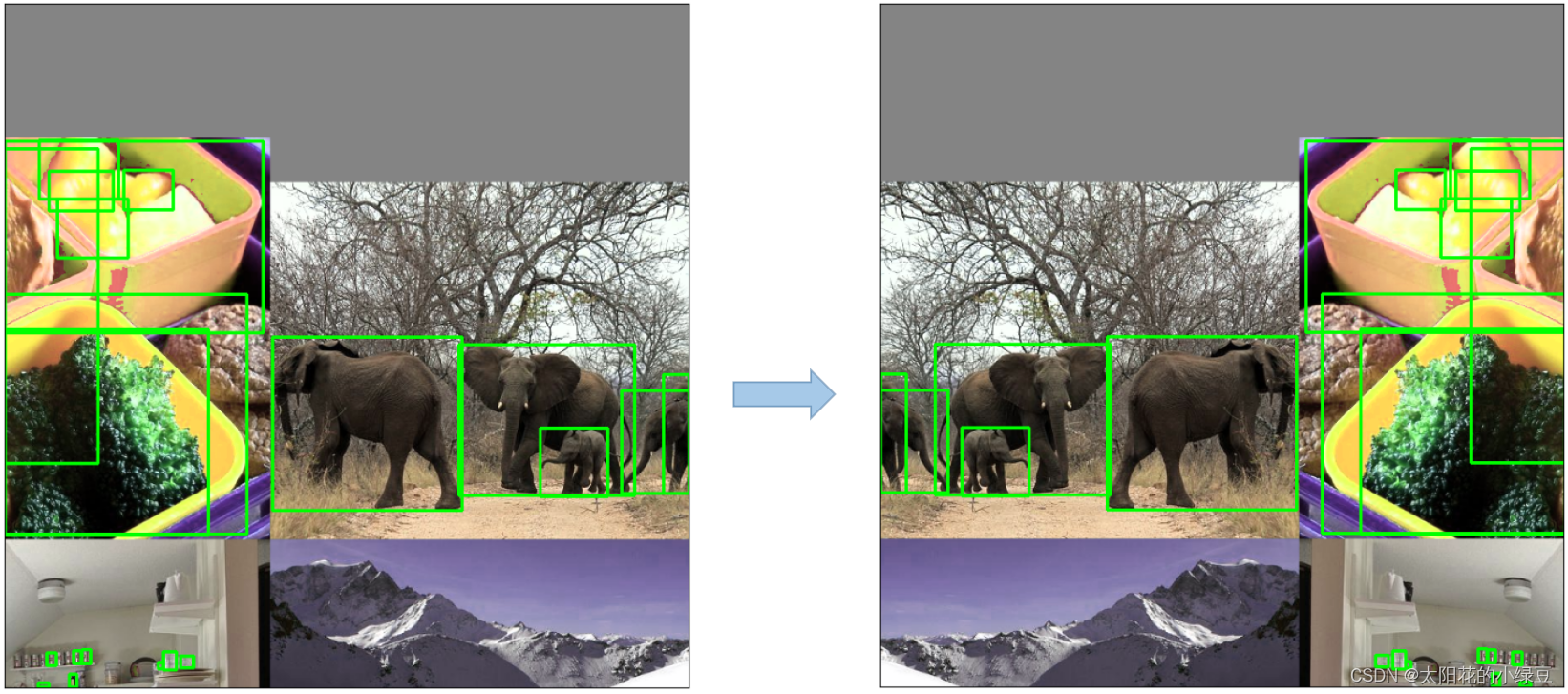
将四张图片拼成一张图片

Copy paste
将部分目标随机粘贴到图片中,前提是数据要有实例分割才可以

Random affine
随即进行仿射变换,其中包括旋转、缩放、平移和裁剪

MixUp
将两张图按照一定的透明度融合在一起
Albumentations
主要是做些滤波、直方图均衡化以及改变图片质量等等
Augment HSV
随机调整色度,饱和度以及明度。

Random horizontal flip
随机水平翻转
-
自适应锚框计算
YOLO算法中,针对不同的数据集,都会有初始设定长宽的锚框,在网络训练中,网络在初始锚框的基础上输出预测框,进而和ground truth进行对比,计算两者差距,再反向更新迭代网络参数。
在YOLOv3、YOLOv4中,训练不同的数据集时,计算初始锚框的值时通过单独的程序运行的,而YOLOv5中将此功能嵌入到代码中,每次训练时,自适应的计算不同训练集中的最佳锚框值。如果在实际训练中感觉计算的锚框修效果不是很好,也可以在代码中将自动计算锚框功能关闭。
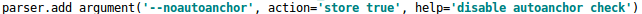
-
自适应图片缩放
在常用的目标检测算法中,不同的图片长宽都不相同,因此常用的方式是将原始图片统一缩放到一个标准尺寸,再送入检测网络中。而YOLOv5中对此做了改进,推理速度得到了37%的提升。 具体思路是由于在项目实际使用中,很多图片的长宽比不同,因此缩放填充后两边的黑边大小都不同,如果填充的太多则会影响推理速度,因此作者在datasets.py的letterbox函数中对此做了修改,对原始图片自适应的添加最少的黑边
第一步:计算缩放比例

第二步:计算缩放后的尺寸

第三步:计算河边填充数值

注意:
- 填充色为灰色**(114,114,114)或者黑色(0,0,0)**效果都一样
- 训练时采用的是传统的填充模式,即缩到416*416并没有采用缩减黑边的方法,只是才推理时才采用了缩减黑边的方式,提高了目标检测的推理速度
- 为什么np.mod函数的后面用32?因为Yolov5的网络经过5次下采样,而2的5次方等于32。所以至少要去掉32的倍数,再进行取余
网络模块
-
yolov5s.yaml参数
-
Parameters
# YOLOv5 🚀 by Ultralytics, GPL-3.0 license # Parameters nc: 80 # number of classes depth_multiple: 0.33 # model depth multiple width_multiple: 0.50 # layer channel multiple anchors: - [10,13, 16,30, 33,23] # P3/8 - [30,61, 62,45, 59,119] # P4/16 - [116,90, 156,198, 373,326] # P5/32- nc:代表数据集中的类别数目
- depth_multiple:控制子模块的数量(depth_multiple * number)仅在number不等于1时启用
- width_multiple:控制卷积核的数量 (width_multiple*args[0])主要作用于args中的ch_out
-
backbone
# YOLOv5 v6.0 backbone backbone: # [from, number, module, args] [[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2 [-1, 1, Conv, [128, 3, 2]], # 1-P2/4 [-1, 3, C3, [128]], [-1, 1, Conv, [256, 3, 2]], # 3-P3/8 [-1, 6, C3, [256]], [-1, 1, Conv, [512, 3, 2]], # 5-P4/16 [-1, 9, C3, [512]], [-1, 1, Conv, [1024, 3, 2]], # 7-P5/32 [-1, 3, C3, [1024]], [-1, 1, SPPF, [1024, 5]], # 9 ]- from:-n代表是从前n层获得的输入
- number:表示网络模块的数目
- module:表示网络模块的名称,具体细节可以在./models/common.py查看
- args:表示向不同模块内传递的参数,即[ch_out, kernel, stride, padding, groups]
-
head
# YOLOv5 v6.0 head head: # [from, number, module, args] [[-1, 1, Conv, [512, 1, 1]], [-1, 1, nn.Upsample, [None, 2, 'nearest']], [[-1, 6], 1, Concat, [1]], # cat backbone P4 [-1, 3, C3, [512, False]], # 13 [-1, 1, Conv, [256, 1, 1]], [-1, 1, nn.Upsample, [None, 2, 'nearest']], [[-1, 4], 1, Concat, [1]], # cat backbone P3 [-1, 3, C3, [256, False]], # 17 (P3/8-small) [-1, 1, Conv, [256, 3, 2]], [[-1, 14], 1, Concat, [1]], # cat head P4 [-1, 3, C3, [512, False]], # 20 (P4/16-medium) [-1, 1, Conv, [512, 3, 2]], [[-1, 10], 1, Concat, [1]], # cat head P5 [-1, 3, C3, [1024, False]], # 23 (P5/32-large) [[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5) ]
-
-
Backbone
-
Focus模块
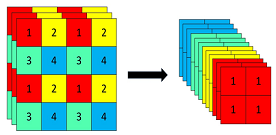
Focus模块在YOLOv5中在图片进入backbone前对图片进行切片。具体操作是在一张图片中每隔一个像素拿到一个值,类似于邻近下采样,这样就拿到了四张图片,四张图片互补,长的差不多,但是没有信息丢失,这样W,H通道缩减为原来的一半但是输入通道扩充了4倍,即拼接起来的图片相对于原先的RGB三通道模式变成了12个通道,最后将得到的新图片再经过卷积操作,最终得到了没有信息丢失情况下的二倍下采样特征图。
以yolov5s为例,原始的640 × 640 × 3的图像输入Focus结构,采用切片操作,先变成320 × 320 × 12的特征图,再经过一次卷积操作,最终变成320 × 320 × 32的特征图。
yolov5作者认为Focus的作用是:减少层数、减少参数量、减少计算量、减少cuda内存占用,在mAP影响很小的情况下,提升推理速度和梯度反向传播速度。(相较于YOLOv3)作者认为一个Focus层可以抵YOLOv3的3个卷积层。
具体代码实现:
class Focus(nn.Module): # Focus wh information into c-space def __init__(self, c1, c2, k=1, s=1, p=None, g=1, act=True): # ch_in, ch_out, kernel, stride, padding, groups super(Focus, self).__init__() self.conv = Conv(c1 * 4, c2, k, s, p, g, act) # 这里输入通道变成了4倍 def forward(self, x): # x(b,c,w,h) -> y(b,4c,w/2,h/2) return self.conv(torch.cat([x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]], 1)) -
CBS模块
由Conv+Bn+SiLU激活函数三者组成。是YOLOv5网络结构中的基础组件

-
BottleNeck模块
一个标准的BottleNeck模块是由11conv、33conv、残差块组成,该模块有两种结构,第一种是带残差块的结构,另外一种是不带残差块仅由11conv和33conv组成的结构。具体结构图示如下所示。
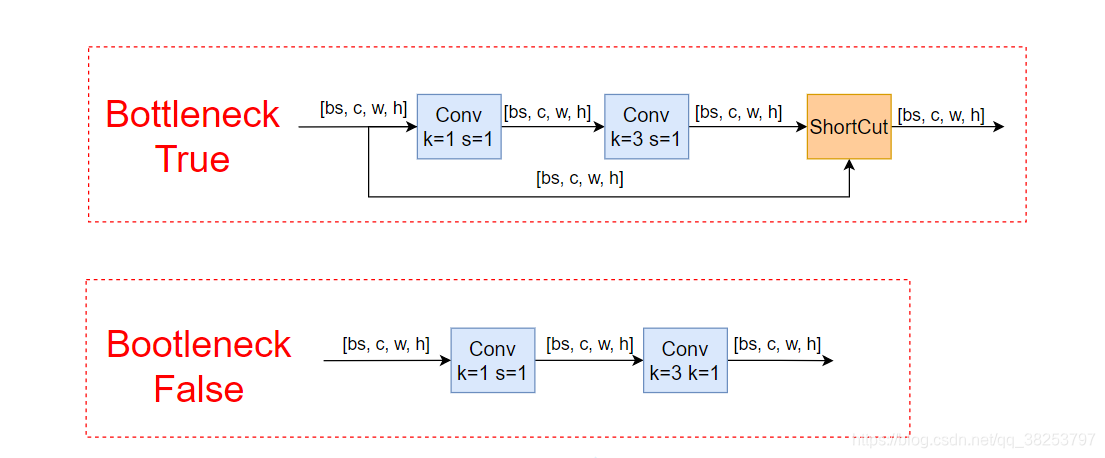
-
CSP1_X模块→C3_1模块CSP1_X:
CSP模块是基于BottleNeck模块的基础上进行改进的模块。YOLOv4在BackBone网络中使用了CSP结构,而YOLOv5在BackBone中同样使用了CSP结构。以YOLOv5s网络为例,CSP1_X结构应用于
Backbone主干网络,另一种CSP2_X结构应用于Neck中。

C3_1:C3模块用来替换
BottleneckCSP模块,从下图可以看出C3相对于BottleneckCSP模块,减少了以一个1*1的conv层,同时撤掉了一个BN层和激活层。结果就是在模型的性能没有下降的同时,模型参数略微下降,推理时间缩短,mAP有小幅度提升(在COCO数据集上的实验结果。)下图所示的ResUnit即为YOLOv5中的bottleneck模块

-
SPP→SPPF模块SPP:
- SPP是将输入并行通过多个不同大小的
MaxPool,然后做进一步融合,能在一定程度上解决目标多尺度问题。
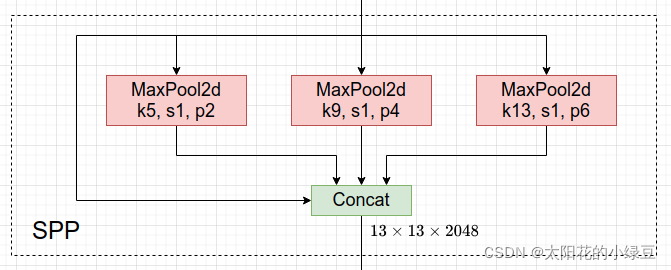
class SPP(nn.Module): def __init__(self): super().__init__() self.maxpool1 = nn.MaxPool2d(5, 1, padding=2) self.maxpool2 = nn.MaxPool2d(9, 1, padding=4) self.maxpool3 = nn.MaxPool2d(13, 1, padding=6) def forward(self, x): o1 = self.maxpool1(x) o2 = self.maxpool2(x) o3 = self.maxpool3(x) return torch.cat([x, o1, o2, o3], dim=1)SPPF:
- SPPF结构是将输入串行通过多个5*5大小的
MaxPool层。
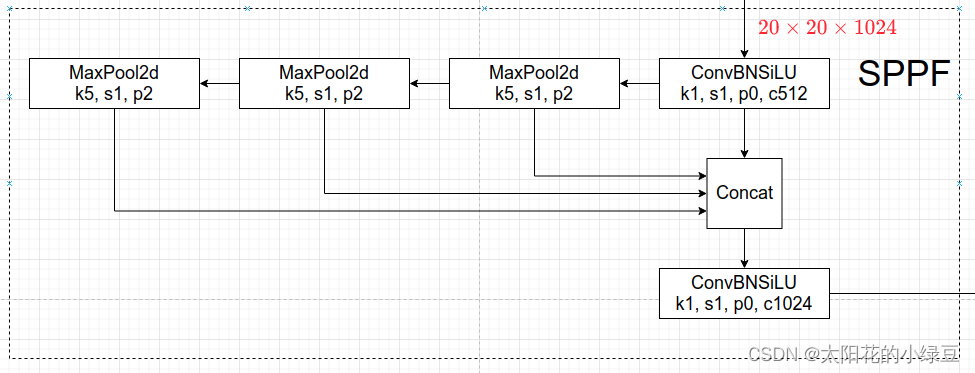
class SPPF(nn.Module): def __init__(self): super().__init__() self.maxpool = nn.MaxPool2d(5, 1, padding=2) def forward(self, x): o1 = self.maxpool(x) o2 = self.maxpool(o1) o3 = self.maxpool(o2) return torch.cat([x, o1, o2, o3], dim=1)SPP VS SPPF:
对比SPP与SPPF的计算结果以及速度(代码上将SPPF中最开始和结尾处的1*1卷积层给去掉,只对比含有
MaxPool的部分):import time import torch import torch.nn as nn class SPP(nn.Module): def __init__(self): super().__init__() self.maxpool1 = nn.MaxPool2d(5, 1, padding=2) self.maxpool2 = nn.MaxPool2d(9, 1, padding=4) self.maxpool3 = nn.MaxPool2d(13, 1, padding=6) def forward(self, x): o1 = self.maxpool1(x) o2 = self.maxpool2(x) o3 = self.maxpool3(x) return torch.cat([x, o1, o2, o3], dim=1) class SPPF(nn.Module): def __init__(self): super().__init__() self.maxpool = nn.MaxPool2d(5, 1, padding=2) def forward(self, x): o1 = self.maxpool(x) o2 = self.maxpool(o1) o3 = self.maxpool(o2) return torch.cat([x, o1, o2, o3], dim=1) def main(): input_tensor = torch.rand(8, 32, 16, 16) spp = SPP() sppf = SPPF() output1 = spp(input_tensor) output2 = sppf(input_tensor) print(torch.equal(output1, output2)) t_start = time.time() for _ in range(100): spp(input_tensor) print(f"spp time: {time.time() - t_start}") t_start = time.time() for _ in range(100): sppf(input_tensor) print(f"sppf time: {time.time() - t_start}") if __name__ == '__main__': main()最终输出结果:

由上图结果可以看出SPP和SPPF的计算结果一致,但是SPPF运行速度比SPP要快上两倍多。
- SPP是将输入并行通过多个不同大小的
-
-
Neck
-
FPN+PAN
YOLOv5目前的Neck和YOLOv4中一样都采用了FPN+PAN的结构,但是在YOLOv5刚出来时只使用了FPN结构,后续才加入了PAN结构。这种结合操作FPN层自顶向下传达强语义特征,而特征金字塔则自底向上传达强定位特征,两两联手,从不同的主干层对不同的检测层进行参数聚合
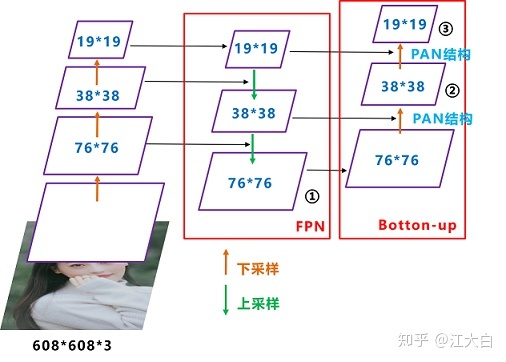
-
CSP2_X模块→C3_2模块CSP2:
YOLOv4的Neck结构中采用的都是普通的卷积操作,而在YOLOv5的Neck结构中,采用借鉴CSPNet设计的CSP2结构,增强了网络特征融合的能力

C3_2:
此处采用的C3与Backbone中的C3模块略有不同,此处的C3用普通的CBS模块替代了Backbone中C3的残差块

-
-
Head输出端
-
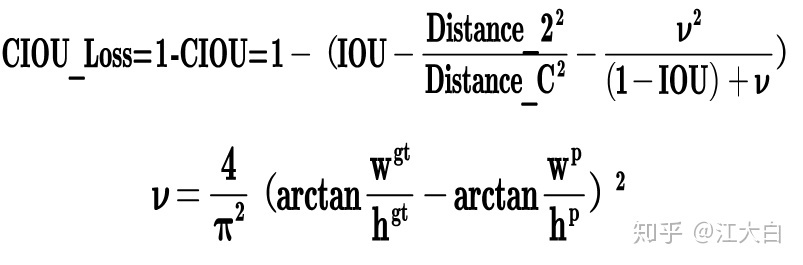
Bounding box损失函数
YOLOv5和YOLOv4同样使用了CIOU_LOSS做Bounding box的损失函数

-
nms非极大值抑制
在目标检测的后处理过程中,针对很多目标框的筛选,通常需要nms操作,因为CIOU_Loss中包含影响因子v,涉及
ground truth的信息,而测试推理时,是没有ground truth的。YOLOv4在DIOU_Loss的基础上采用DIOU_nms的方式,而YOLOv5则采用了加权nms的方式(CIOU_Loss+DIOU_nms),由下图可以看出,采用DIOU_Loss,原本被遮挡的摩托车也可以被检测出来(黄色箭头部分)
-
其他细节
-
BCELoss和BCEWithLogitsLoss
BCELoss和BCEWithLogitsLoss是一组常用的二元交叉熵损失函数,常用于二分类问题。区别在于BCELoss的输入需要先进行Sigmoid处理,而BCEWithLogitsLoss则是将Sigmoid和BCELoss合成一步,也就是说BCEWithLogitsLoss函数内部自动先对output进行Sigmoid处理,再对output和target进行BCELoss计算。

BCELoss需要将data_input事先sigmoid好才能用,而BCEWithLogitsLoss会帮你sigmoid,如下:(运行结果可以看出两者的输出值是一样的)
input = torch.randn(3)#随机生成一个输入,没有被sigmoid。 target=torch.Tensor([0., 1., 1.]) loss1=nn.BCELoss() loss2=nn.BCEWithLogitsLoss() print("BCELoss:",loss1(torch.sigmoid(input), target))#需要sigmod print("BCEWithLogitsLoss:",loss2(input,target))#不需要sigmoid
-
损失函数计算
YOLOv5的损失只要由三个部分组成:(λ1,λ2,λ3为平衡系数)下图中zxy为矩阵维度[3,80,80]


分类损失和定位损失使用二元交叉熵损失函数
BCEWithLogitsLoss计算。置信度损失计算使用CIoU函数计算-
Classes Loss:分类损失,采用的是
BCE Loss,这里只计算正样本的分类损失。-
网络对8080网格的每个格子都预测三个预测框,每个预测框的预测信息都包含了N个分类概率。其中N为总类别数,最终会组成一个[38080N]的概率矩阵
-
为了减少过拟合,且增加训练的稳定性,通常对独热码标签做一个平滑操作。如下式,label为独热码中的所有数值,α为平滑系数,取值范围0~1,通常取0.1

-
-
Objectness Loss:
obj损失,采用BCE Loss,这里的obj指的是网络预测的目标边界框与ground truth的CIOU。这里计算的是所有样本的obj损失-
YOLO之前版本直接对mask矩阵为true的地方赋值1,mask矩阵为false的地方赋值0,mask为true只表示预测框在目标附近,并不一定完美包围了目标。yolov5改变了做法:对mask为true的位置计算对应预测框与目标框的CIOU,使用CIOU作为该预测框的置信度标签,当然对mask为false的位置还是直接赋0。这样标签值的大小与预测框、目标框的重合度有关,两框重合度越高则标签值越大。但是CIOU的取值范围是-1.51,而置信度标签的取值范围是01,所以需要对CIOU做一个截断处理:当CIOU小于0时直接取0值作为标签。
-
假设置信度标签为矩阵L,预测置信度为矩阵P,那么矩阵中每个数值的BCE loss的计算公式如下

-
CIOU Tips
-
CIOU公式

-
初始版本的YOLOv5:
- 原论文CIoU损失在实现上做了一点小调整, 在求导时a作为常数项不参与梯度更新, 只针对v里的w和h分别求导, 会得到如下图式

-
其中w2+h2通常会由于w或者h太小而造成反向传播的时候梯度爆炸, 所以原作者最初版本的实现如下
with torch.no_grad(): arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1) v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2) S = 1 - iou alpha = v / (S + v) w_temp = 2 * w1 ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1) cious = iou - (u + alpha * ar)其中
alpha和v均不参与梯度更新, 只有ar处直接写成了求导形式, 最后对w,h求导只会剩下h,-w,没有w2+h2
-
YOLOv5 6v_x
-
在最新的CIOU实现上改为如下:
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2) with torch.no_grad(): S = 1 - iou alpha = v / (S + v) cious = iou - (u + alpha * v) cious = torch.clamp(cious,min=-1.0,max = 1.0)同样的
alpha不参与参数的梯度更新, 只是作为一个常数, 但是v的修改已经默认了不对w2+h2问题做额外处理, 早期的版本虽然兼顾了w2+h2对最终梯度问题的影响, 反向传播形式没变, 但是正向表达式中的v变了, yolov5由于对wh有做进一步筛选, 所以避免了w2+h2过小对梯度的影响。
-
-
-
-
-
Location Loss:定位损失,采用的是
CIOU Loss,只计算正样本的定位损失(IOU、GIOU、DIOU、CIOU)

-
-
平衡不同尺度的损失
这里针对三个预测特征层
(p3, p4, p5)上的obj损失采用不同的权重,在源码中,针对预测小目标的预测特征层(p3)采用的权重是4.0,针对预测中等目标的预测特征层(p4)采用的权重是1.0,针对预测大目标的预测特征层(P5)采用的权重是0.4,这个是针对COCO数据集设置的超参数
-
消除Grid敏感度
在YOLOv4中主要是调整预测目标中心点相对
Grid Cell的左上角偏移量。下图是YOLOv2,v3的计算公式。
-
t
x
t_x
tx?是网络预测的目标中心
x坐标偏移量(相对于网格的左上角) -
t
y
t_y
ty?是网络预测的目标中心
y坐标偏移量(相对于网格的左上角) -
c
x
c_x
cx?是对应网格左上角的
x坐标 -
c
y
c_y
cy?是对应网格左上角的
y坐标 -
σ
\sigma
σ是
Sigmoid激活函数,将预测的偏移量限制在 0 到 1 之间,即预测的中心点不会超出对应Grid Cell区域
调整一:
关于预测目标中心点相对
Grid Cell左上角 ( ? c x ? *c_x* ?cx?? , c y c_y cy? ) 偏移量为 σ ( t x ) \sigma(t_x) σ(tx?), σ ( t x ) \sigma(t_x) σ(tx?) 。YOLOv4 的作者认为这样做不太合理,**比如当真实目标中心点非常靠近网格的左上角点( σ ( t x ) \sigma(t_x) σ(tx?)和 σ ( t y ) \sigma(t_y) σ(ty?)应该趋近于 0 )或者右下角点( σ ( t x ) \sigma(t_x) σ(tx?)和 σ ( t y ) \sigma(t_y) σ(ty?)应该趋近于 1 )时,网络的预测值需要负无穷或者正无穷时才能取到,而这种很极端的值网络一般无法达到。**为了解决这个问题,作者对偏移量进行了缩放从原来的( 0 , 1 ) 缩放到( ?0.5 , 1.5 ) 这样网络预测的偏移量就能很方便达到 0 或 1,故最终预测的目标中心点 b x b_x bx?, b y b_y by? 的计算公式为:
下图是绘制的 y = σ ( x ) y = \sigma(x) y=σ(x)对应**
before曲线和 y = 2 ? σ ( x ) ? 0.5 y = 2 \cdot \sigma(x) - 0.5 y=2?σ(x)?0.5对应after**曲线,很明显通过引入缩放系数scale以后,y 对x 更敏感了,且偏移的范围由原来的( 0 , 1 ) 调整到了( ?0.5 , 1.5 )。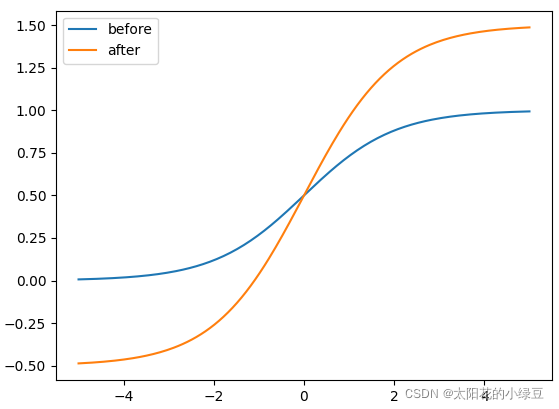
调整二:
YOLOv5中除了调整预测
Anchor相对Grid Cell左上角 ( c x , c y ) (c_x, c_y) (cx?,cy?) 偏移量以外,还调整了预测目标高宽的计算公式,调整后的公式为:
作者的意思是,原来的计算公式并没有对预测目标宽高做限制,这样可能出现梯度爆炸,训练不稳定等问题。下图是修改前 y = e x y = e^x y=ex和修改后 y = ( 2 ? σ ( x ) ) 2 y = (2 \cdot \sigma(x))^2 y=(2?σ(x))2(相对Anchor宽高的倍率因子)的变化曲线, 很明显调整后倍率因子被限制在( 0 , 4 ) 之间。
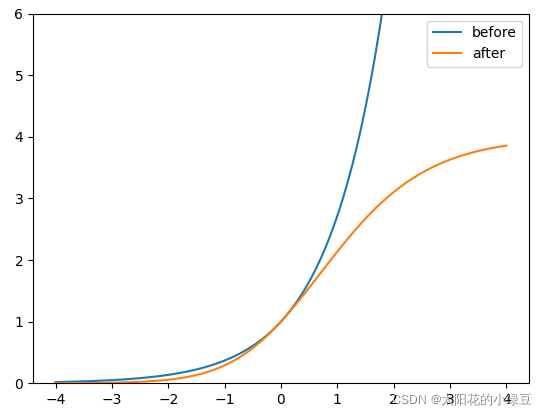
-
t
x
t_x
tx?是网络预测的目标中心
-
匹配正样本(Build Targets)
YOLOv4中是直接将每个
ground truth box与对应的Anchor Templates模板计算IoU,只要IoU
大于设定的阈值就算匹配成功。但在YOLOv5中,作者先去计算每个ground truth box与对应的Anchor Templates模板的高宽比例,即:r w = w g t / w a t r h ? = h g t ? / h a t ? r_w=w_{gt}/w_{at} \\ r_h?=h_{gt?}/h_{at?} rw?=wgt?/wat?rh??=hgt??/hat??
然后统计这些比例和它们倒数之间的最大值,这里可以理解成计算
GT Box和Anchor Templates
分别在宽度以及高度方向的最大差异(当相等的时候比例为1,差异最小):r w m a x = m a x ( r w , 1 / r w ) r h m a x = m a x ( r h , 1 / r h ) r_w^{max} = max(r_w, 1 / r_w) \\ r_h^{max} = max(r_h, 1 / r_h) rwmax?=max(rw?,1/rw?)rhmax?=max(rh?,1/rh?)
接着统计 r w m a x r_w^{max} rwmax?和 r h m a x r_h^{max} rhmax?之间的最大值,即宽度和高度方向差异最大的值:
r m a x = m a x ( r w m a x , r h m a x ) r^{max} = max(r_w^{max}, r_h^{max}) rmax=max(rwmax?,rhmax?)
如果
ground truth box和对应的Anchor Template的 r m a x r^{max} rmax小于阈值anchor_t(在源码中默认设置为4.0),即ground truth box和对应的Anchor Template的高、宽比例相差不算太大,则将ground truth box分配给该Anchor Template模板。为了方便大家理解,可以看下我画的图。假设对某个ground truth box而言,其实只要ground truth box满足在某个Anchor Template宽和高的 × 0.25 \times 0.25 ×0.25倍和 × 4.0 \times4.0 ×4.0倍之间就算匹配成功。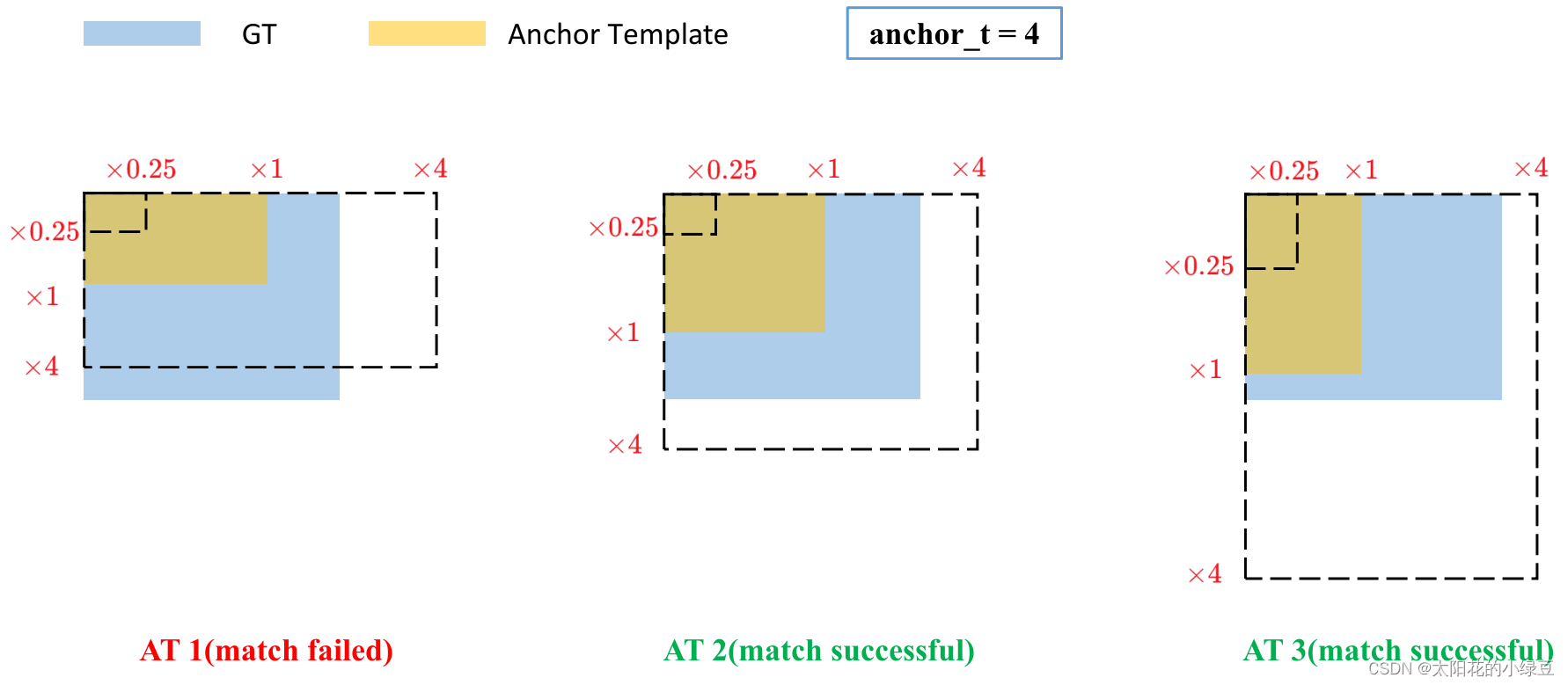
剩下的步骤和YOLOv4中一致:
-
将
ground truth投影到对应预测特征层上,根据ground truth的中心点定位到对应Cell,注意图中有三个对应的Cell。因为网络预测中心点的偏移范围已经调整到了( ?0.5 , 1.5 ) ,所以按理说只要Grid Cell左上角点距离ground truth中心点在( ?0.5 , 1.5 )范围内它们对应的Anchor都能回归到ground truth的位置处。这样会让正样本的数量得到大量的扩充。 -
则这三个
Cell对应的AT2和AT3都为正样本。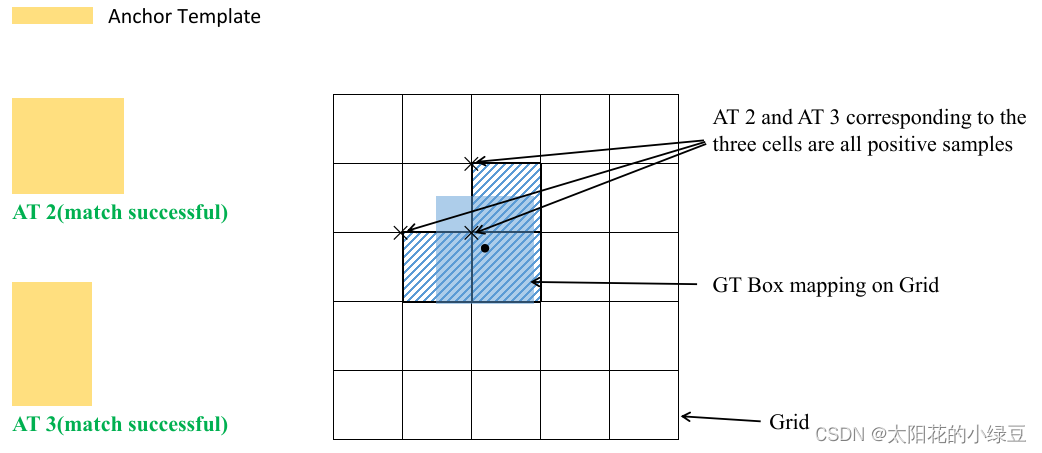
还需要注意的是,YOLOv5源码中扩展
Cell时只会往上、下、左、右四个方向扩展,不会往左上、右上、左下、右下方向扩展。下面又给出了一些根据 G T x c e n t e r , G T y c e n t e r GT_x^{center}, GT_y^{center} GTxcenter?,GTycenter? 的位置扩展的一些Cell案例,其中 %1 %1 表示取余并保留小数部分。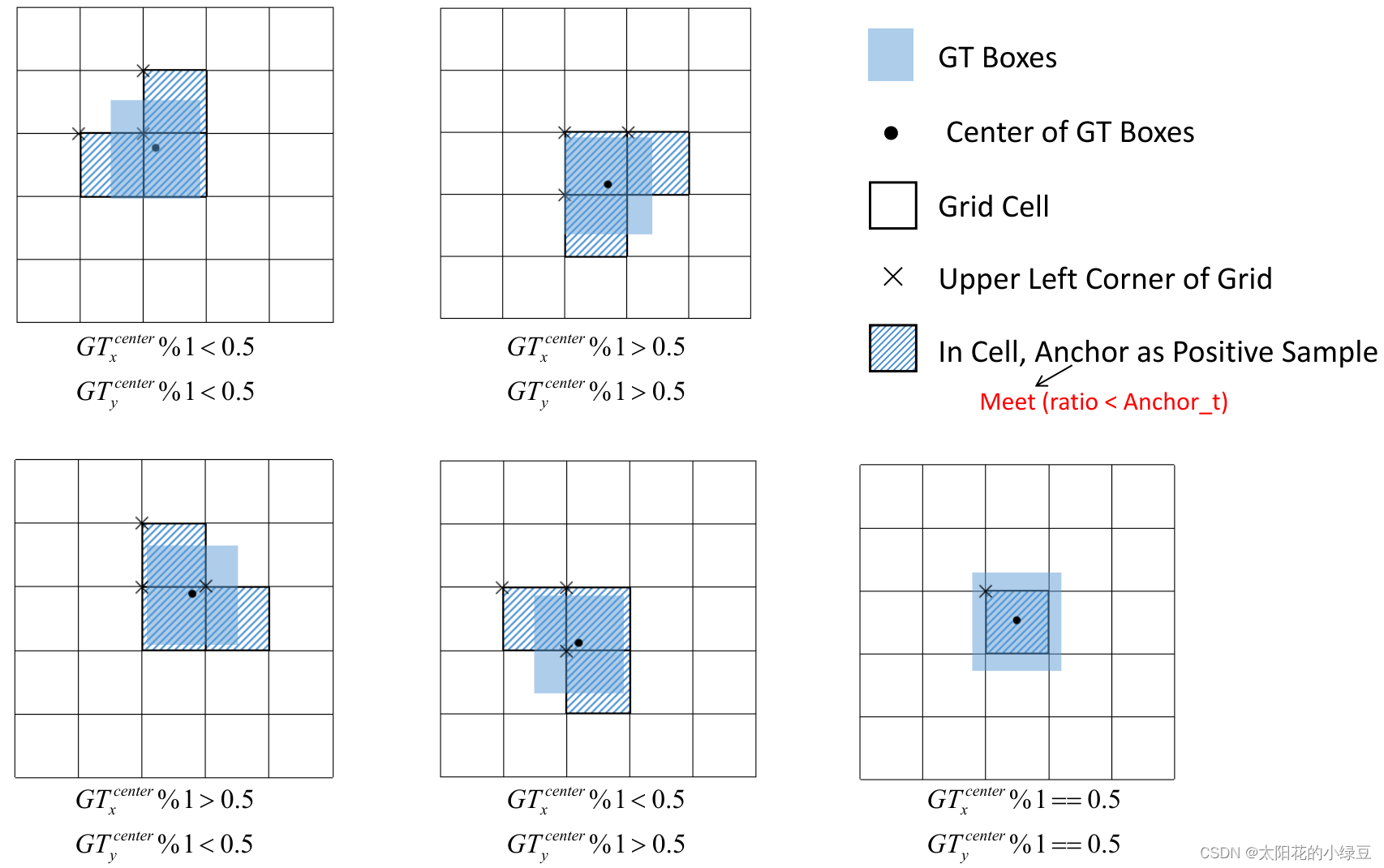
-
-
标签平滑(Label Smoothing)
假设分类有两个,一个是猫一个不是猫,分别用0和1表示。Label smoothing的工作原理是对原来的[0, 1]这种标注做一个改动,假设我们给定Label Smoothing的平滑参数为0.1: [0, 1]*(1-0.1)+0.1/2 = [0.05, 0.95]
可以看到,原来的[0,1]标签成了[ 0.05 , 0.95 ]了,那么就是说,原来分类准确的时候,p = 1 ,不准确为p = 0。假设为Label Smoothing的平滑参数为?,现在变成了: 分类准确的时候 p = 1 ? 0.5 ? ? p=1-0.5*\epsilon p=1?0.5??, 分类不准确时 p = 0.5 ? ? p=0.5*\epsilon p=0.5??,也就是说对分类准确做了一点惩罚。
这实际上是一种正则化策略,减少了真实样本标签的类别在计算损失函数时的权重,最终起到抑制过拟合的效果。
下图为使用Label Smoothing的概率分布图:

-
IOU、GIOU、DIOU、CIOU
-
IOU

IoU就是我们所说的交并比,是目标检测中最常用的指标,在anchor-based的方法中,他的作用不仅用来确定正样本和负样本,还可以用来评价输出框(
predict box)和ground-truth的距离。- 它可以反映预测检测框与真实检测框的检测效果
- 一个很好的特性就是尺度不变性,也就是对尺度不敏感
-
GIOU
GIOU:《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》

-
GIoU在IoU的基础上考虑多了非交叉面积比例, 如上图红色虚线框就是A,B边框的最小包围框,灰色斜线面积占整个红色边框面积就是非交叉面积占比 -
对比
L2 Loss,IoU和GIoU具有尺度不变性, 意味着当目标边框等比放大时,损失能依旧保持同样的量级, 无需针对大小不同边框分别处理。 -
对比
IoU Loss,L2和GIoU具有偏离趋势度量能力, 如左下图, 传统IoU=0时,边框距离的远近已经对最终损失都是一样, 但是GIoU随着两个边框距离越远,表现得越接近-1, 换算成损失就是越大, 同样GIoU会驱使模型预测边框分布于真实边框的上下左右方向, 对斜方向预测结果施加更大损失,如右下图所示。
-
GIoU的损失值域空间为[0,2], 当完美拟合损失0, 当距离无限远且不交叉时,损失是2
-
-
DIOU
DIoU: 《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》

DIoU损失在1-IoU的基础上, 增加了中心点距离占比惩罚项, 其中惩罚项分子是预测边框中心点与真实边框中心点的距离, 分母是预测边框与真实边框的最小包围框对角线长, 如下图d和c

-
对比
GIoU Loss,DIoU能更好度量预测边框和真实边框的中心点距离和方向, 表现如下图所示,绿色真实边框, 红色预测边框, 当预测边框与真实边框互相包含, 或者互相垂直交叉, 水平交叉,GIoU会退化成为IoU, 从而失去非交叉占比的惩罚项, 而DIoU依旧能为模型提供更好的梯度方向

-
与
GIoU Loss一样,DIoU也具有尺度不变性, 意味着当目标边框等比放大时, 损失能依旧保持同样的量级, 无需针对大小不同边框分别处理 -
与
GIoU损失一样,DIoU损失值域空间为[0,2], 当完美拟合损失0, 当距离无限远且不交叉时,损失是2
-
-
CIOU
CIoU: 《Enhancing Geometric Factors in Model Learning and Inference for Object Detection and InstanceSegmentation》
CIoU损失在DIoU的基础上, 增加了宽高比惩罚项, 其中v为真实边框与预测边框的宽高比损失, α \alpha α为宽高比损失系数

-
对比
DIoU Loss, 当预测边框和真实边框的中心点重合,CIoU具有更好的宽高拟合效果, 如下图所示 , 预测边框与真实边框中心点重合,DIoU损失中的中心点距离惩罚项=0,DIoU损失退化成IoU损失, 但是此时CIoU仍有宽高比损失惩罚, 能进一步调整宽高比例
-
CIoU综合了IoU的交叉面积占比损失,DIoU的中心点偏移损失, 以及自身宽高比损失3种度量优点
-
-
-
多尺度训练
如果网络的输入是416 x 416。那么训练的时候就会从 0.5 x 416 到 1.5 x 416 中任意取值,但所取的值都是32的整数倍。
-
自适应Anchor(AutoAnchor)
通过 k-means聚类 + 遗传算法来生成和当前数据集匹配度更高的anchors,如果需要在自己的数据集上训练,则可以使用AutoAnchor策略
-
预热(Warmup)
训练开始前会使用 warmup 进行训练。在模型预训练阶段,先使用较小的学习率训练一些epochs或者steps (如4个 epoch 或10000个 step),再修改为预先设置的学习率进行训练。
Warmup的作用:
- 有助于减缓模型在初始阶段对mini-batch的提前过拟合现象,保持分布的平稳
- 有助于保持模型深层的稳定性
-
学习率调整策略(Cosine LR scheduler)
余弦退火衰减
引入学习率衰减的定义(训练神经网络时一般需要调整学习率,随着epoch的增加,学习率不断衰减),学习率如果太大,容易发生震荡,此时需要调小学习率,如果学习率太小,则训练的时间太长。学习率衰减yolov5中采用余弦退火方式。(快照集成)
严格的说,余弦退火策略不应该算是学习率衰减策略,因为它使得学习率按照周期变化

-
动量(EMA)
采用了 EMA 更新权重,相当于训练时给参数赋予一个动量,这样更新起来就会更加平滑
-
混合精度训练(Mixed precision)
使用了 amp 进行混合精度训练。能够减少显存的占用并且加快训练速度,但是需要 GPU 支持
后续问题收集处理
-
问题一:在训练阶段三个anchor都求Loss还是只求一个最大的Loss
Classes Loss 计算正样本损失(计算所有正样本Loss, 并非每个grid cell 中都会有一个anchor)
Objectness Loss 计算所有样本损失(计算所有grid cell中所有anchor的Loss)
Location Loss 计算正样本损失(同上)
loss.py class ComputeLoss: sort_obj_iou = False # Compute losses def __init__(self, model, autobalance=False):... def __call__(self, p, targets): # predictions, targets # #初始化各个损失 lcls = torch.zeros(1, device=self.device) # class loss lbox = torch.zeros(1, device=self.device) # box loss lobj = torch.zeros(1, device=self.device) # object loss # 获取正样本anchor的标签分类、坐标框信息、索引值,以及anchor的尺寸 # [198, 289, 280] **tcls, tbox, indices, anchors = self.build_targets(p, targets) # targets 获得标签分类,边框,索引,anchors** # Losses 遍历三个尺度层的预测输出 for i, pi in enumerate(p): # layer index, layer predictions # b表示当前bbox属于batch内部的第几张图片, # a表示当前bbox和当前层的第几个anchor匹配上, # gi,gj是对应的负责预测该bbox的网格坐标 **b, a, gj, gi = indices[i] # image, anchor, gridy, gridx** tobj = torch.zeros(pi.shape[:4], dtype=pi.dtype, device=self.device) # target obj n = b.shape[0] # number of targets if n: # 根据对应正样本的位置信息取出相应位置的预测值 # [198, 289, 280] 对应3次for循环 **pxy, pwh, _, pcls = pi[b, a, gj, gi].split((2, 2, 1, self.nc), 1) # target-subset of predictions 找到对应网格的输出,取出对应位置预测值** # Regression 目标框回归 pxy = **pxy**.sigmoid() * 2 - 0.5 # [198*2, 289*2, 280*2] pwh = (**pwh**.sigmoid() * 2) ** 2 * anchors[i] # [198*2, 289*2, 280*2] **pbox** = torch.cat((pxy, pwh), 1) # predicted box # 正样本anchor的iou值 总数(198+289+280) **iou = bbox_iou(pbox, tbox[i], CIoU=True).squeeze() # iou(prediction, target) 计算边框损失,计算的是CIOU** **lbox += (1.0 - iou).mean()** # 定位损失 # Objectness 置信度损失 iou = iou.detach().clamp(0).type(tobj.dtype) if self.sort_obj_iou: j = iou.argsort() b, a, gj, gi, iou = b[j], a[j], gj[j], gi[j], iou[j] if self.gr < 1: iou = (1.0 - self.gr) + self.gr * iou # 获取正样本anchor赋值IOU,其余anchor的IOU值为0 tobj[b, a, gj, gi] = iou # iou ratio # Classification 分类损失 if self.nc > 1: # cls loss (only if multiple classes) 类别数大于1 # [198*80, 289*80, 280*80] t = torch.full_like(**pcls**, self.cn, device=self.device) # targets t[range(n), tcls[i]] = self.cp lcls += self.BCEcls(pcls, t) # BCE 分别对每个类别计算loss **obji = self.BCEobj(pi[..., 4], tobj) # [1*3*80*80, 1*3*40*40, 1*3*20*20] lobj += obji * self.balance[i] # obj loss** if self.autobalance: self.balance[i] = self.balance[i] * 0.9999 + 0.0001 / obji.detach().item() if self.autobalance: self.balance = [x / self.balance[self.ssi] for x in self.balance] # 根据超参数设置的各个部分损失的系数获取最终的损失 lbox *= self.hyp['box'] lobj *= self.hyp['obj'] lcls *= self.hyp['cls'] bs = tobj.shape[0] # batch size return (lbox + lobj + lcls) * bs, torch.cat((lbox, lobj, lcls)).detach() -
问题二:cls和cls_pw的详细含义
box: 0.02 #定位损失的系数 cls: 0.21638 #分类损失的系数 cls_pw: 0.5 #分类BCELoss中正样本的权重 obj: 0.51728 #有无物体损失的系数 obj_pw: 0.67198 #有无物体BCELoss中正样本的权重-
cls_pw 和obj_pw
可以通过向正例添加权重来权衡召回率和精度。在多标签分类的情况下,损失可以描述为:
? c ? ( x , y ) = L c ? = { l 1 , c ? , … , l N , c ? } ? , l n , c ? = ? w n , c ? [ p c ? y n , c ? ? l o g σ ( x n , c ? ) + ( 1 ? y n , c ? ) ? l o g ( 1 ? σ ( x n , c ? ) ) ] ?c?(x,y)=Lc?=\{l_{1,c}?,…,l_{N,c?}\}?,l_{n,c}?=?w_{n,c}?[p_c?y_{n,c}??logσ(x_{n,c}?)+(1?y_{n,c}?)?log(1?σ(x_{n,c}?))] ?c?(x,y)=Lc?={l1,c??,…,lN,c??}?,ln,c??=?wn,c??[pc??yn,c???logσ(xn,c??)+(1?yn,c??)?log(1?σ(xn,c??))]
? ( x , y ) = { m e a n ( L ) , if?reduction=‘mean’; s u m ( L ) , if?reduction=‘sum’. ?(x,y)=\begin{cases}mean(L),& \text{if reduction=‘mean’;}\\sum(L),& \text{if reduction=‘sum’.}\end{cases} ?(x,y)={mean(L),sum(L),?if?reduction=‘mean’;if?reduction=‘sum’.?
c是标签数量(c>1用于多标签的二元分类,c=1用于单标签的二元分类),n是batch size p c p_c pc?是正样本的权重用来权衡召回率和精度, p c p_c pc?>1时增加召回率, p c p_c pc?<1时增加精度
例如,如果数据集包含单个类的 100 个正样本和 300 个负样本,则该类的 pos_weight 应等于 300 100 = 3 \frac{300}{100}=3 100300?=3 。损失将表现为数据集包含 3×100=300 个正例。
-
box、cls和obj
在train.py中会通过段代码调节三个损失的各自权重
# Model parameters hyp['box'] *= 3 / nl # 通过检测层数来缩放box系数 hyp['cls'] *= nc / 80 * 3 / nl # 通过检测层数和类别数缩放cls系数 hyp['obj'] *= (imgsz / 640) ** 2 * 3 / nl # 通过类别数和图像尺寸来缩放obj系数最后分别计算三种Loss并将其加权Loss求和
lbox *= self.hyp['box'] lobj *= self.hyp['obj'] lcls *= self.hyp['cls'] bs = tobj.shape[0] # batch size return (lbox + lobj + lcls) * bs, torch.cat((lbox, lobj, lcls)).detach()
-
-
问题三:batch NMS和NMS的区别
#如果agnostic为True则执行NMS,如果为False则执行batch NMS c = x[:, 5:6] * (0 if agnostic else max_wh) # 类别序号乘以7680 max_wh boxes, scores = x[:, :4] + c, x[:, 4] # boxes在所有的坐标上加上了7680*类别序号,目的是为了将不同类别的boxes分离开 scores类别概率 i = torchvision.ops.nms(boxes, scores, iou_thres) # NMS 对bouding boxes索引进行降序排列,选中一个框,遍历其他的框与这个框做IOU,如果IOU大于某个阈值则将遍历的这个框删除(同一个物体) if i.shape[0] > max_det: # 判断是否超出最大检测数 i = i[:max_det] if merge and (1 < n < 3E3): # Merge NMS (boxes merged using weighted mean) # update boxes as boxes(i,4) = weights(i,n) * boxes(n,4) iou = box_iou(boxes[i], boxes) > iou_thres # iou matrix weights = iou * scores[None] # box weights x[i, :4] = torch.mm(weights, x[:, :4]).float() / weights.sum(1, keepdim=True) # merged boxes if redundant: i = i[iou.sum(1) > 1] # require redundancy-
batched_nms():
根据每个类别进行过滤,只对同一种类别进行计算IOU和阈值过滤
-
nms():
不区分类别对所有bbox进行过滤。如果有不同类别的bbox重叠的话会导致被过滤掉并不会分开计算。
-