【知识蒸馏2018】Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons
?? 论文: https://arxiv.org/pdf/1811.03233.pdf
一 主要思想:
??让教师网络层的神经元的激活边界尽量和学生网络的一样。所谓的激活边界指的是分离超平面(针对的是RELU这种激活函数),其决定了神经元的激活与失活。本文提出的激活转移损失,让教师网络与学生网络之间的分离边界尽可能一致。
二 问题来源及推导模型:
1. 问题及推导
??

??
??定义: 教师网络到最后隐藏层的函数T,相应学生为S(在激活函数之前)。为了方便,先假设教师学生最后隐藏层具有相同尺寸大小为RM。
??针对图片I,相应有T(I),S(I)
∈
\in
∈ RM。
??
??以前使用的损失函数中如下(1):

??其中激活函数
σ
(
x
)
=
m
a
x
(
0
,
x
)
\sigma(x)=max(0,x)
σ(x)=max(0,x)。
??
??

??产生的问题: 损失(1)使学生仅仅近似老师的神经元反应,但结果的激活边界可能有很大的不同。尤其是不好区分弱反应和强反应。
??
??
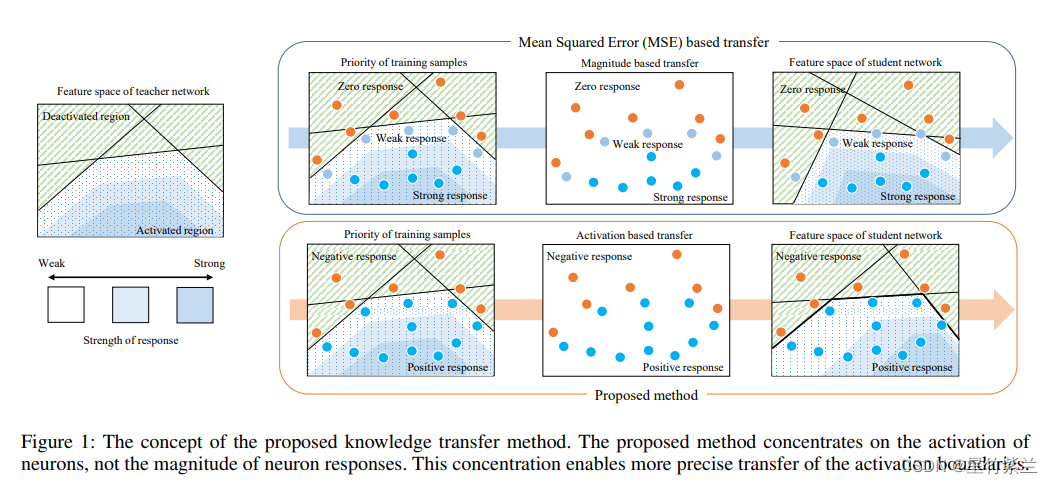
??为了准确地转移激活边界,我们的想法是放大在激活边界附近区域的可忽略的转移损失。为了放大损失,我们定义了一个元素激活指示器函数来表示:

??图1的下半部分显示了使用激活转移损失的知识转移。虽然神经元反应的大小没有很好地传递,但它被训练以保持教师神经元的激活。因此,激活边界被准确地传递。考虑到激活边界在神经网络中的重要性,激活传递损失在知识传递中比均方误差更有效。
??由于ρ()是一个离散函数,激活转移损失不能通过梯度下降最小化。因此,我们提出了一个可被梯度下降最小化的替代损失。
??最小化激活转移损失类似于学习二值分类器。
?? 如果教师神经元是活跃的则学生神经元的反应应大于0;如果教师神经元是不活跃的,则小于0。借鉴了hinge loss:
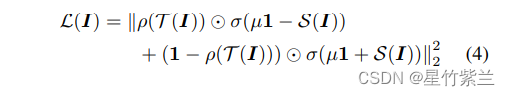
??
2.补充:
??1).当老师和学生的最后尺寸不一致时,添加联通函数r:

??
??
??2).卷积网络同样适用。

??
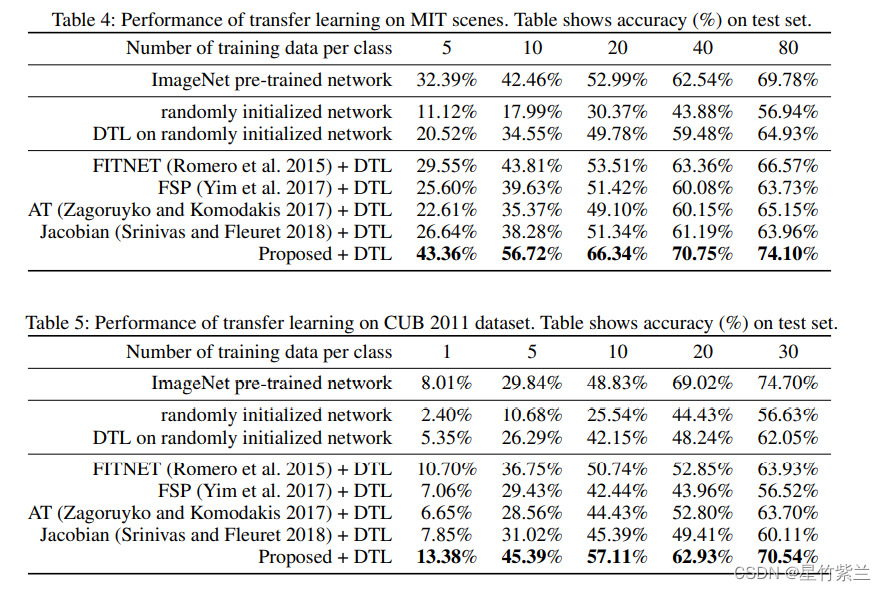
三 实验结果:
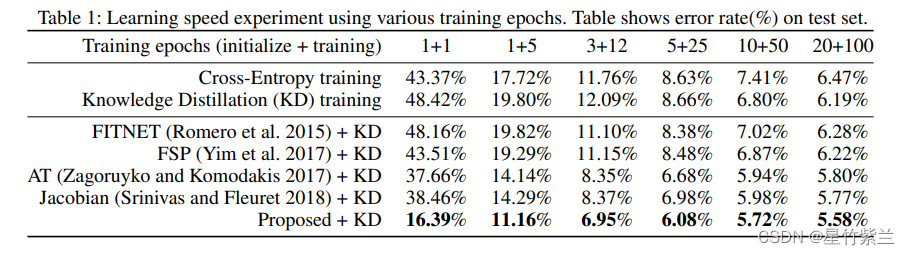
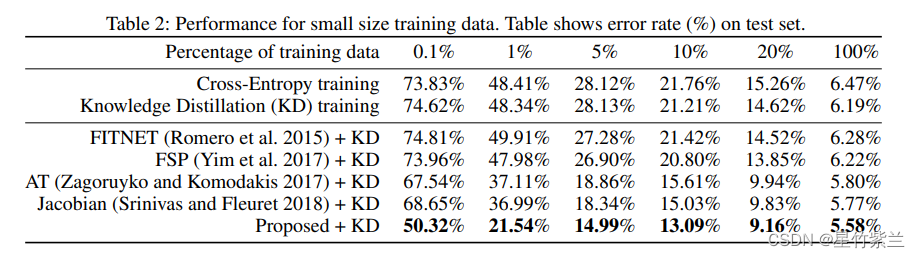
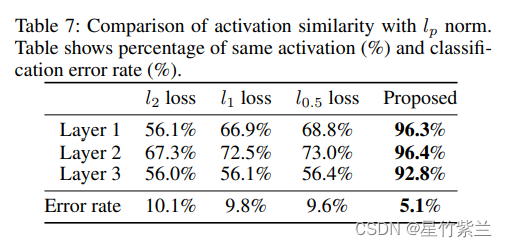
??关于本文提出的替代损失是否使神经元激活相似。为了进行比较,我们还评估了l1和l0.5的损失函数,以及l2的损失。
??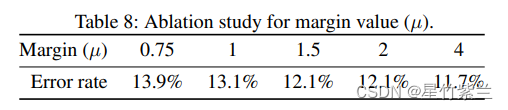
??最后对边缘值μ进行了消融研究。