目前,有多种技术可用于机器学习检测概念漂移的方法。熟悉这些检测方法是为每个漂移和模型使用正确度量的关键。
在本文章中,回顾了四种类型的检测方法:统计、统计过程控制、基于时间窗口和上下文方法。
如果您正在寻找有关概念漂移的介绍,我建议您查看机器学习中的概念漂移一文。
统计方法
统计方法用于比较分布之间的差异。
在某些情况下,会使用散度,这是分布之间的一种距离度量。 在其他情况下,运行测试以获得分数。
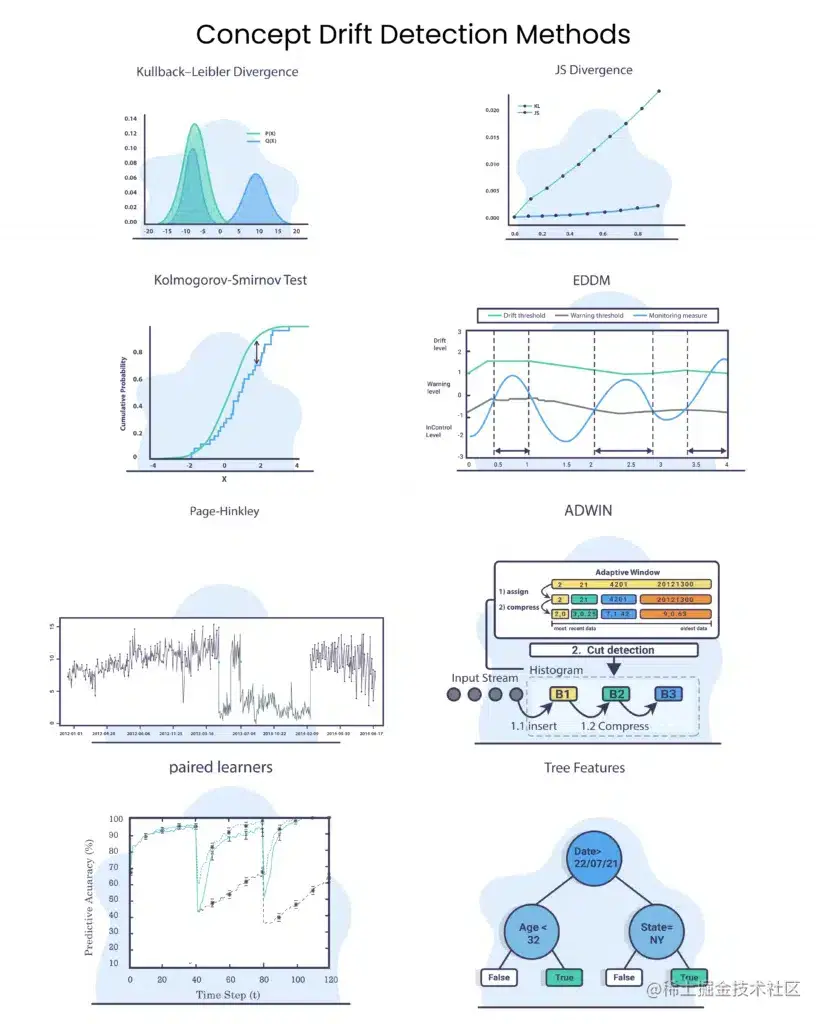
Kullback-Leibler 散度
Kullback-Leibler 散度有时被称为相对熵。
KL散度试图量化一个概率分布与另一个概率分布有多大不同,所以,如果我们有分布Q和P,其中,Q分布是旧数据的分布,P是我们想要计算的新数据的分布:
K L ( Q ∣ ∣ P ) = ? ∑ x P ( x ) ? l o g ( Q ( x ) P ( x ) ) KL(Q||P) = - \displaystyle\sum_x{P(x)}*log(\frac{Q(x)}{P(x)}) KL(Q∣∣P)=?x∑?P(x)?log(P(x)Q(x)?)
其中,“||”代表散度。
我们可以看到,
- 如果 P(x) 高而 Q(x) 低,则散度将很高。
- 如果 P(x) 低而 Q(x) 高,则散度也会很高,但不会那么大。
- 如果 P(x) 和 Q(x) 相似,则散度就会很低。
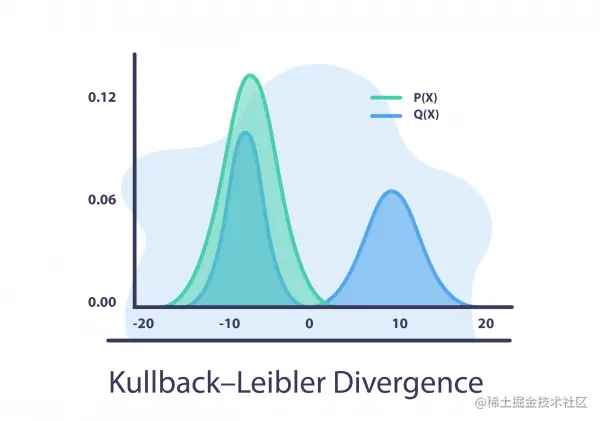
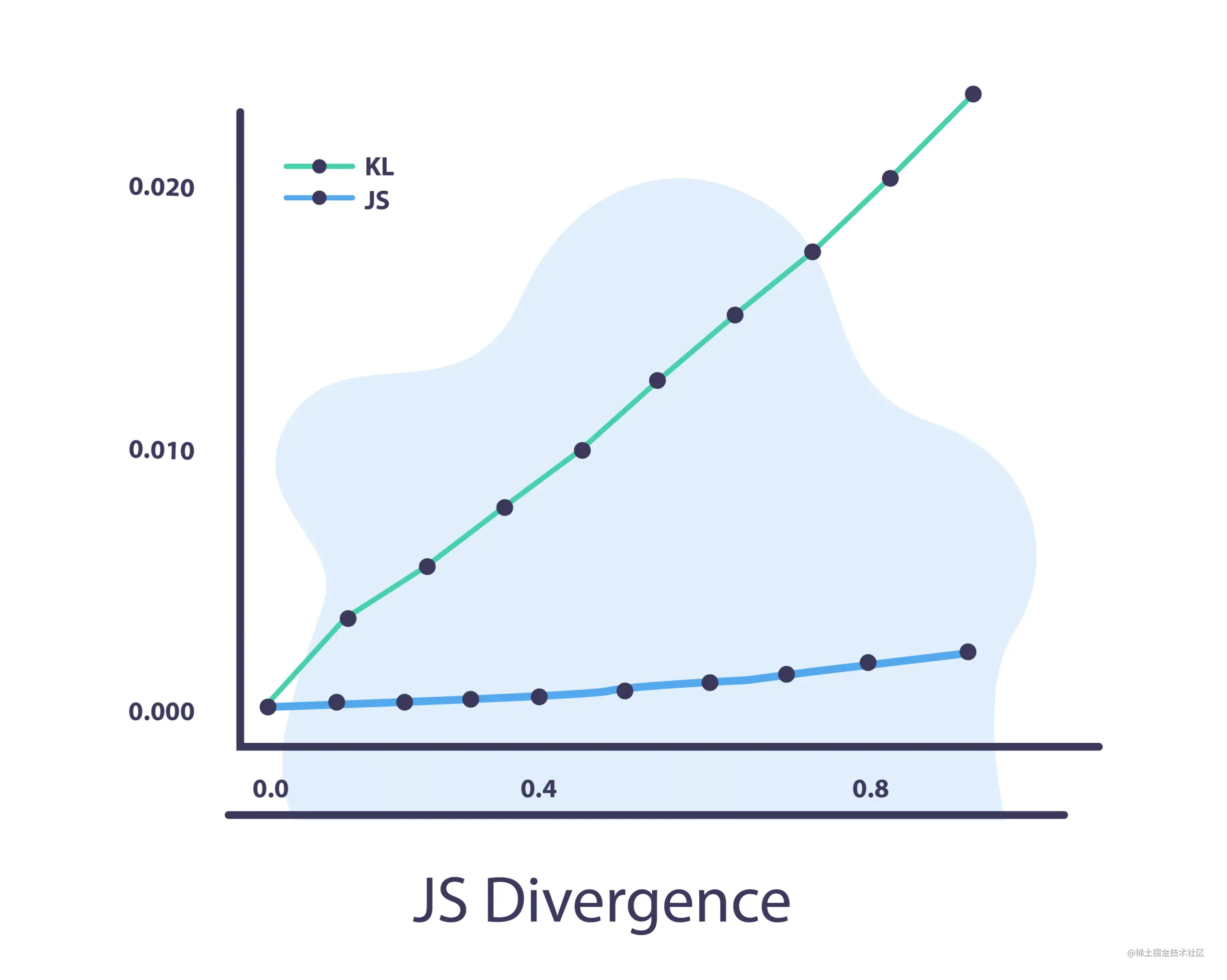
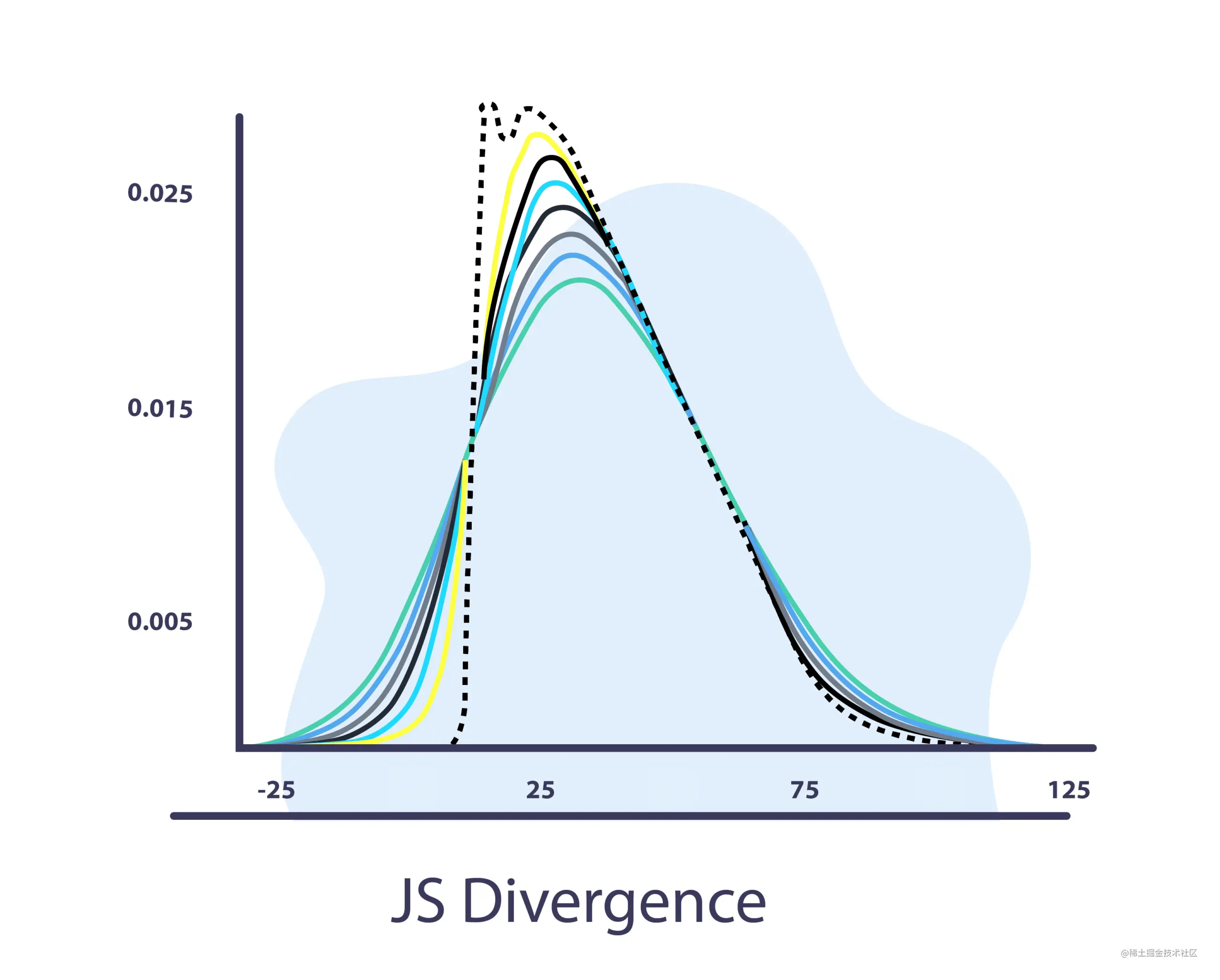
JS 散度
Jensen-Shannon 散度使用 KL 散度
J S ( Q ∣ ∣ P ) = 1 2 ( K L ( Q ∣ ∣ M ) + K L ( P ∣ ∣ M ) ) JS(Q||P) = \frac{1}{2}(KL(Q||M) +KL(P||M)) JS(Q∣∣P)=21?(KL(Q∣∣M)+KL(P∣∣M))
其中, M = Q + P 2 M = \frac{Q+P}{2} M=2Q+P? 是 P 和 Q 之间的平均值。
JS散度和KL散度的主要区别在于JS是对称的,它总是有一个有限值。
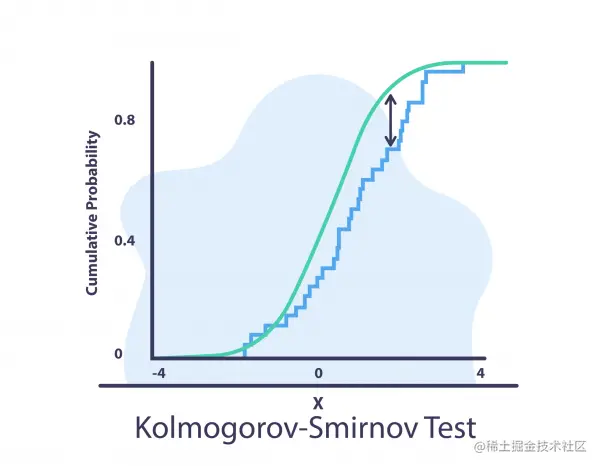
Kolmogorov-Smirnov 检验 (K-S 检验)
两样本 KS 检验是比较两个样本的有用且通用的非参数方法。 在 KS 测试中,我们计算:
D
n
,
m
=
s
u
p
x
∣
F
1
,
n
(
x
)
?
F
2
,
m
(
x
)
∣
D_{n,m}=sup_{x}|F_{1,n}(x) - F_{2,m}(x)|
Dn,m?=supx?∣F1,n?(x)?F2,m?(x)∣
其中, F 1 , n ( x ) F_{1,n}(x) F1,n?(x) 是先前数据与 n n n 样本的经验分布函数, F 2 , m ( x ) F_{2,m}(x) F2,m?(x) 是新数据与 m m m 样本和 F n ( x ) = 1 n ∑ i = 1 n I [ ? ∞ , x ] ( X i ) F_{n}(x) = \frac{1}{n} \displaystyle\sum_{i=1}^n I_{[- \infty,x]}(X_{i}) Fn?(x)=n1?i=1∑n?I[?∞,x]?(Xi?)的经验分布函数, s u p x sup_{x} supx? 是使 ∣ F 1 , n ( x ) ? F 2 , m ( x ) ∣ |F_{1,n}(x) - F_{2,m}(x)| ∣F1,n?(x)?F2,m?(x)∣ 最大化的样本 x x x 的子集。
KS 检验对两个样本的经验累积分布函数的位置和形状的差异很敏感。它非常适合数值数据。
何时使用统计方法
统计方法部分的想法是评估两个数据集之间的分布。
我们可以使用这些工具来查找不同时间范围内的数据之间的差异,并衡量随着时间的推移数据行为的差异。
对于这些方法,不需要标签,也不需要额外的内存,我们可以快速获得模型输入特征/输出变化的指标。 这将帮助我们甚至在模型的性能指标出现任何潜在下降之前就开始调查这种情况。 另一方面,如果没有正确处理,缺少标签和忽视对过去事件和其他特征的记忆可能会导致误报。
统计过程控制
统计过程控制的想法是验证我们模型的误差是否在可控范围内。 这在生产中运行时尤其重要,因为性能会随着时间而变化。因此,我们希望有一个系统,如果模型达到了一定错误率,就会发送警报。请注意,某些模型具有“红绿灯”系统,其中也有警告报警。
漂移检测方法/早期漂移检测方法 (DDM/EDDM)
这个想法是将误差建模为二项式变量。 这意味着我们可以计算出我们的预期误差值。 当我们使用二项式分布时,我们可以标记 = n p t =npt =npt,因此, σ = p t ( 1 ? p t ) n \sigma = \sqrt{\frac{p_{t}(1-p_{t})}{n}} σ=npt?(1?pt?)??。
DDM
在这里我们可以提出:
- 当 p t + σ t ≥ p m i n + 2 σ m i n p_{t}+\sigma_{t}\ge p_{min} +2\sigma_{min} pt?+σt?≥pmin?+2σmin? 时发出警告
- 当 p t + σ t ≥ p m i n + 3 σ m i n p_{t}+\sigma_{t}\ge p_{min} +3\sigma_{min} pt?+σt?≥pmin?+3σmin? 时报警
优点:DDM 在检测逐渐变化(如果它们不是很慢)和突然变化(增量和突然漂移)时表现出良好的性能。
缺点:当变化缓慢时,DDM 难以检测漂移。许多样本可能在漂移水平激活之前储存了很长时间,存在样本储存溢出的风险。
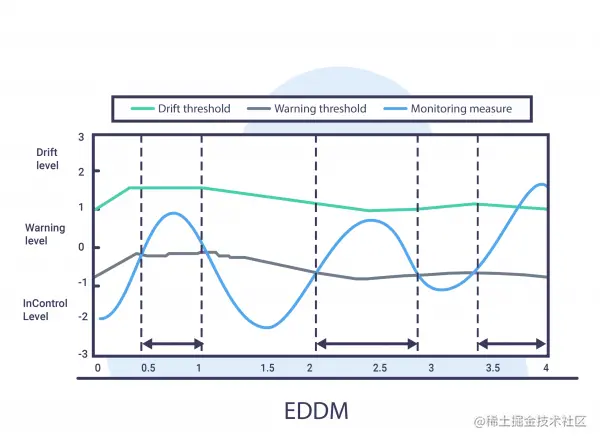
EDDM
在这里,通过测量 2 个连续错误的距离,我们可以提出:
- 当 p t + 2 σ t p m a x + 2 σ m a x < α \frac{p_{t}+2{\large \sigma}_{t}}{p_{max}+2{\large \sigma}_{max}}<{\Large \alpha} pmax?+2σmax?pt?+2σt??<α 时发出警告
- 当 p t + 2 σ t p m a x + 2 σ m a x < β \frac{p_{t}+2{\large \sigma}_{t}}{p_{max}+2{\large \sigma}_{max}}<{\Large \beta} pmax?+2σmax?pt?+2σt??<β 时发出警报,其中 ${\Large \beta} $ 通常为 0.9
EDDM 方法是 DDM 的修改版本,其重点是识别逐渐漂移。
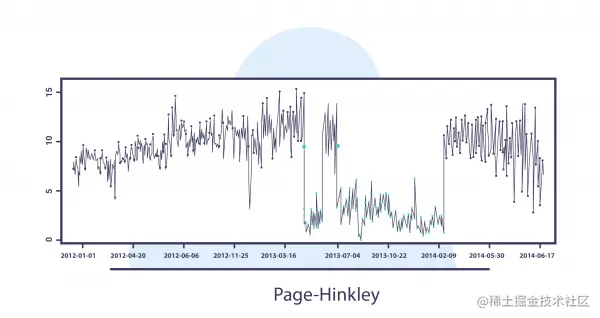
CUMSUM 和 Page-Hinckley (PH)
CUSUM 及其变体 Page-Hinckley (PH) 是社区中的开拓方法之一。 该方法的想法是提供一种序列分析技术,该技术通常用于监测高斯信号平均值的变化检测。
CUSUM 和 Page-Hinckley (PH) 通过计算观测值与平均值的差异来检测概念漂移,并在该值大于用户定义的阈值时设置漂移警报。 这些算法对参数值很敏感,导致在误报和检测真实漂移之间进行权衡。
由于 CUMSUM 和 Page-Hinckley (PH) 用于处理数据流,因此每个事件都用于计算下一个结果:
CUMSUM:
- g 0 = 0 , g t = m a x ( 0 , g t ? 1 + ε t ? v ) {\large g}_{0}=0, {\large g}_{t}= max(0, {\large g}_{t-1}+{\large \varepsilon}_{t}-{\large v}) g0?=0,gt?=max(0,gt?1?+εt??v) 其中, g 代表事件,或出于漂移目的,模型的输入/输出
- 当 g t > h {\large g}_{t}>h gt?>h 发出警报,并设置 g t = 0 {\large g}_{t}=0 gt?=0
- h , v h,v h,v 是可调参数
注意:CUMSUM 是无记忆的、单边的或不对称的,因此它只能检测到值的增加。
Page-Hinckley (PH) :
- g 0 = 0 , g t = g t ? 1 + ( ε t ? v ) {\large g}_{0}=0, {\large g}_{t}= {\large g}_{t-1}+({\large \varepsilon}_{t}-v) g0?=0,gt?=gt?1?+(εt??v)
-
G
t
=
m
i
n
(
g
t
,
G
t
?
1
)
G_{t}=min({\large g}_{t},G_{t-1})
Gt?=min(gt?,Gt?1?)
当 g t ? G t > h g_{t}-G_{t}>h gt??Gt?>h 发出警报,并设置 g t = 0 g_{t}=0 gt?=0。
何时使用统计过程控制方法
要使用所介绍的统计过程控制方法,我们需要提供样本的标签。 在许多情况下,这可能是一个挑战,因为延迟可能很高,并且很难提取它,尤其是在大型组织中使用它时。 另一方面,一旦获得这些数据,我们就会得到一个相对快速的系统来涵盖 3 种漂移类型:突然漂移、渐进漂移和增量漂移。
该系统还允许我们与部门一起跟踪退化情况(如果有的话),以发出警告和警报。
时间窗口分布
时间窗口分布模型关注时间戳和事件的发生。
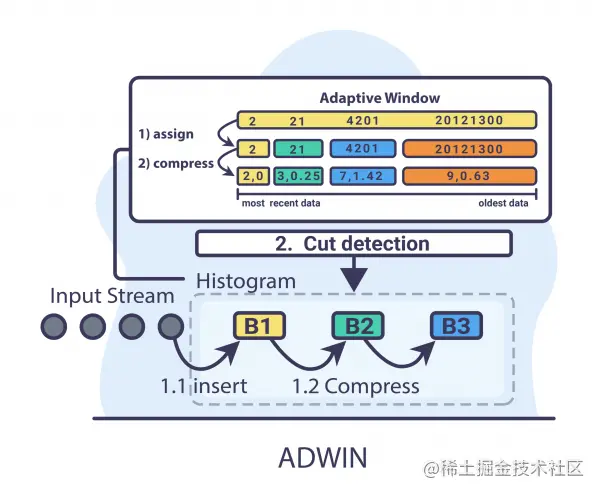
ADWIN
ADWIN 的思想是从时间窗口 W W W 开始,在上下文没有明显变化时动态增大窗口 W W W,并在检测到变化时将其缩小。 该算法试图找到显示不同平均值的 W ? w 0 W - w_{0} W?w0? 和 w 1 w_{1} w1? 的两个子窗口。 这意味着窗口的旧部分 ? w 0 - w_{0} ?w0? 是基于与实际不同的数据分布,因此被删除。
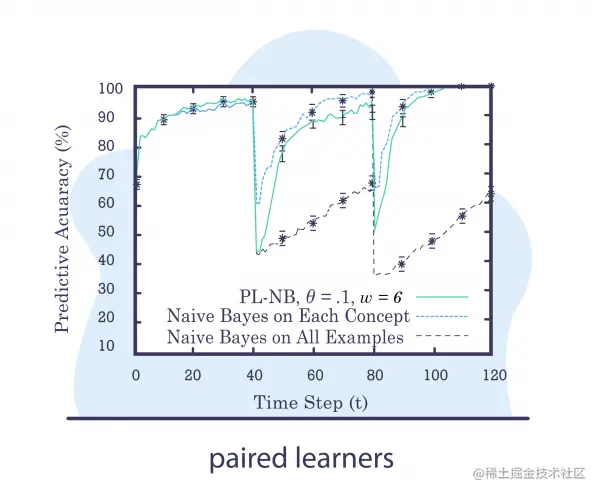
Paired Learners
假设对于给定的问题,我们有一个使用大量数据进行训练的大型稳定模型,让我们将其标记为模型 A。
我们还将设计另一个模型,一个更轻量级的模型,在更小和更新的数据上进行训练(它可以具有相同的类型)。 我们将其称为模型 B。
想法:找到模型 B 优于模型 A 的时间窗口。由于模型 A 比模型 B 稳定并且封装了更多数据,我们预计它会胜过它。 但是,如果模型 B 优于模型 A,则可能表明发生了概念漂移。
上下文方法(Contextual Approaches)
这些方法的想法是评估训练集和测试集之间的差异。 当差异显著时,可能表明数据存在漂移。
树特征
树特征的想法是在数据上训练一个相对简单的树,并添加预测时间戳作为特征之一。 由于树模型也可以用于特征重要性,我们可以知道时间如何影响数据以及在什么时候。此外,我们可以查看由时间戳创建的拆分,我们可以看到拆分前后概念之间的差异。
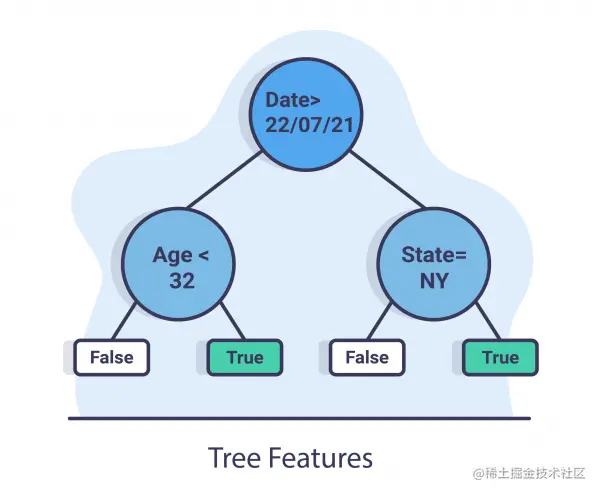
在上图中,我们可以看到日期特征位于根部,这意味着该特征具有最高的信息增益,这意味着在 7 月 22 日,他们可能在数据中发生了漂移。
漂移检测实现
您可以找到相关的提供漂移检测的实现:
- Java 实现:MOA
- Python 实现:scikit-multiflow