[人工智能]TBCNN

• • TBCNN – 基于树的卷积神经网络

    TBCNN: A Tree-Based Convolutional Neural Network for Programming Language Processing

    • 一种用于编程语言处理的基于树的卷积神经网络

    • Abstract:

      • 由于当前还没有将深度神经网络应用于编程语言处理, 提出TBCNN模型来对基于ASTs的编程语言进行建模, 提取丰富的信息
      • 在模型中首先通过基于ASTs的编码准则来预训练获得program vector, 然后通过树型卷积来捕捉树的一些有用特征, 并且引入了三路池化(3-way pooling)和连续二叉树(continous binary tree)来处理不同形状大小的ASTs
      • 通过与基准方法对比, 这个方法可以更好更快地完成程序分类任务, 同时预训练出来的program vector也能提高训练的速度

    • Introduction:

      • 编程语言和自然语言的区别: 程序包含丰富而明确的结构信息, 编程语言中的源代码往往遵循固定僵化的语法结构, 而且通过复杂的控制流和数据流, 批次之间的代码块之间可能存在依赖关系
      • 1. 提出“编码准则”学习ast中每个节点的向量表示，作为预训练阶段;
        2. 提出了基于树的卷积方法提取程序的局部结构特征;
        3. 引入“连续二叉树”和“三路池化”的概念，使模型适用于不同结构和大小的树;

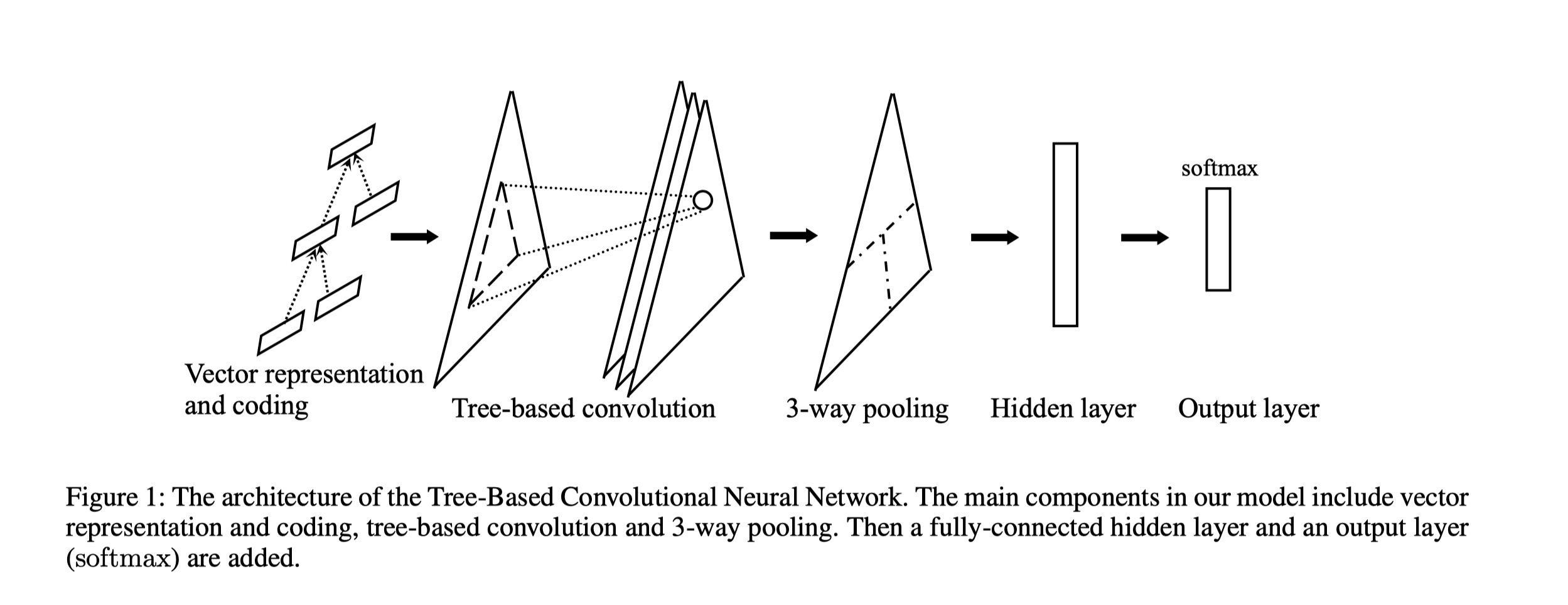
    整体模型

    

    • Pretraining

      • 对于一个节点 $p$ 和它的所有孩子 $c_1,c_2,...,c_i$ ,用一下式子来表示 $p$ 的coded vector

        ? $vec(p)\approx tanh({\sum }_i{l}_i{W}_{code,i}vec(c_i)+b_{code})$

      • 定义 $vec(p)$ 和 $p$ 的 coded vector 的距离的平方

        ? $d={\left|\left|vec(p)?tanh({\sum }_i{l}_i{W}_{code,i}vec(c_i)+b_{code})\right|\right|}_2^2$

      • 同时, 通过将一个随机一个节点($p$ 或者 $p$ 的某一个孩子) 换成一个随机的symbol 来完成负采样, 把这个负样本和其coded vector之间的距离计为 $d_c$

      • 目标: $minimiz{e}_{W_{code}^l,W_{code}^r,b_{c}ode}max(d?d_c+△)$

    • Coding layer

      • 对于非叶子结点, $p=W_{comb1}vec(p)+W_{comb2}tanh({\sum }_i{l}_i{W}_{code,i}vec(x_i)+b_{code}$

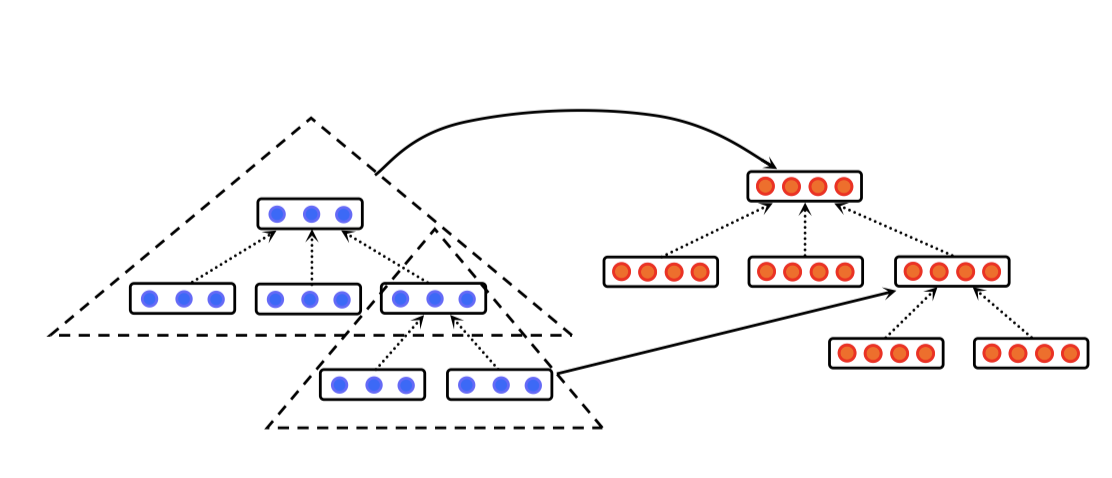
    • Tree-based consolution layer

      

      用固定深度的树型卷积核划过整个树结构, 假定对应节点的向量表示是 $x_1,x_2,...x_n$, 那么这个卷积层的输出是

      $y=tanh({\sum }_n{W}_{code,i}?x_i+b_{code})$

      而由于孩子节点的数量不固定并且树的形状和大小不固定, 这一步需要同时用zero-paddings和连续二叉树的概念

      • 连续二叉树 continuous binary tree

        把目标子树看作是一个二叉树(无论原本是什么形状和大小), 使用三个基本的权重矩阵 $W_{conv}^{left},W_{conv}^{right},W_{conv}^{top}$.

        对于子树中的某一个节点 $x_i$, 其权重矩阵 $W_{conv}$ 是这三个基本权重矩阵的线性组合

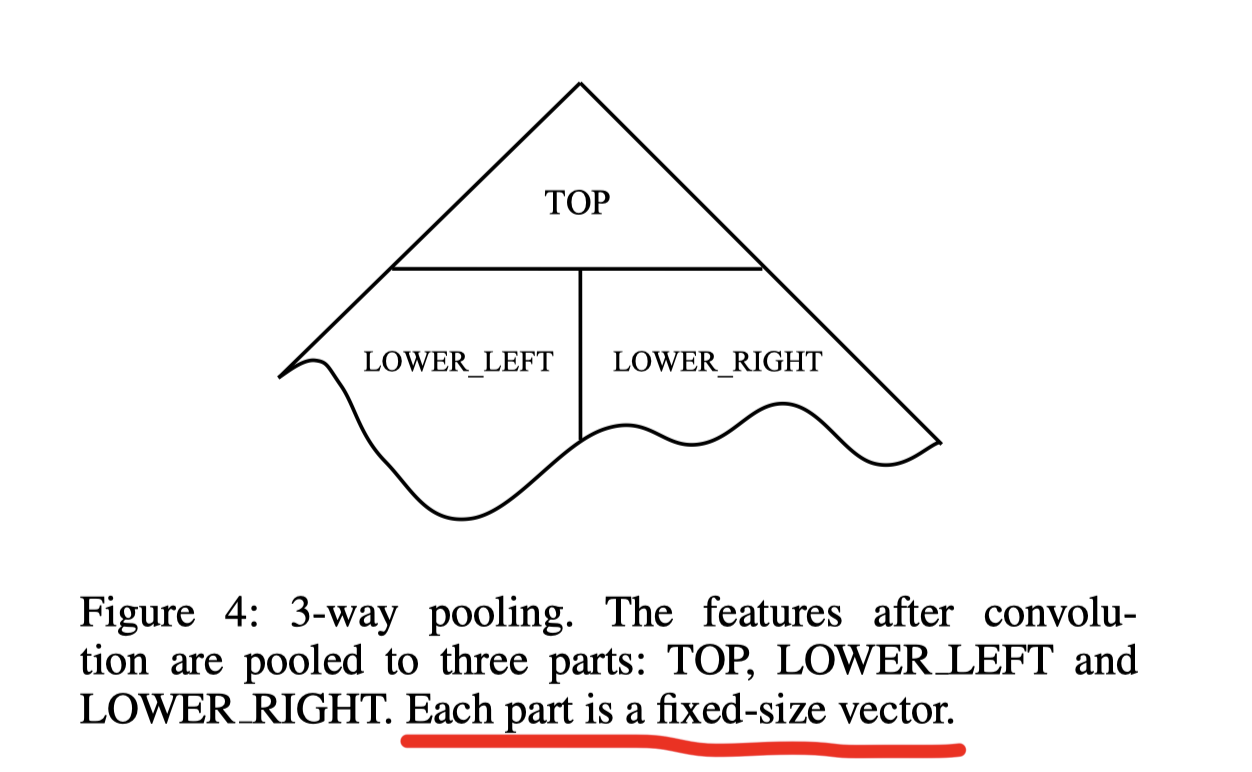
    • Three-way pooling

      ?

      卷积层之后会得到一个形状和大小不变的新树, 因此不能直接接到hidden layer和output layer

      用三路池化讲特征池化成三个部分

    • SGDM 优化器算法

      • 向后传播算法

    • Hiden layer and output layer — softmax

      归一化 $softma{x}_i=\frac{e^i}{{\sum }_j{e}^j}$

    ?

    • 实验和实验结果
      • 向量表示成功地捕获了AST节点的有意义特征
      • 神经编程语言处理, 对程序进行分类是有效可行的