目录
?3、NAG(Nesterov Accelerated Gradient,NAG)
为什么需要优化算法
????????对于几乎所有的机器学习算法,最后一般都可以归结为最优化问题,也就是归结为求一个目标函数的极值问题,因此对于一个确定的损失函数,就需要寻找一个最佳的映射函数
,使得
对输入
映射出的输出
值与真实值
的损失最小,而使得损失最小的那一组参数
就是我们需要的模型参数。
? ? ? ? 不管是机器学习还是深度学习的模型,通常映射函数会非常复杂,甚至包含上千亿参数量,因此,在高维空间中,
的局部极值肯定不止一个,但是全局最小值一定是存在的,局部极值我们称之为局部最优点,全局最小值我们称之为全局最优点,因此我们就希望有一个算法能够帮助我们最大可能的搜索到
的全局最优点(通常这是不可能的),这样的一个算法就称之为优化算法。
梯度下降法
????????梯度下降法沿着梯度的反方向进行搜索,利用了函数的一阶导数信息。梯度下降法的迭代公式为:
![]()
? ? ? ? 梯度的方向为当前函数值上升最快的方向,因此在负梯度方向就是函数值下降最快的方向,把学习率设置为比较小的正数,那么每一次对参数
的更新迭代都会使得函数值变小,在有限次的迭代下,就可以搜寻到局部最优或全局最优。
1、SGD、BGD、MBGD
????????随机梯度下降(Stochastic Gradient Descent, SGD)每次从训练样本随机抽取一个样本计算loss和梯度并对参数进行更新,由于每次只是对某一个样本计算loss,所以每次迭代速度快。但是这种优化算法比较弱,因为每次随机选择的样本并不能代表所有的样本,往往容易走偏,反而会增加很多次的迭代。随机梯度下降法有时可以用于在线学习(Online Learning)系统,可使系统快速学习到新的变化。
????????批量梯度下降(Batch Gradient Descent,BGD),每次使用整个训练集合所有样本计算loss和梯度,这样计算的梯度比较稳定,因为所有样本当然能代表所有样本,相比随机梯度下降法不那么容易振荡,但是因为每次都需要更新整个数据集,所以批量梯度下降法非常慢,而且无法放在内存中计算,更无法应用于在线学习系统,(注意BGD和SGD虽然每次迭代选取的样本数量不同,但是在反向传播梯度时都是传播一次,慢的只是计算loss的时间不同)。
????????小批量随机梯度下降法(Mini-Batch Gradient Descent)是对批量梯度下降以及随机梯度下降的一个折中办法,其思想是:每次迭代随机抽取batch_size个样本来计算loss和梯度,这里折中的也就是计算loss的时间。
? ? ? ? 随机梯度下降法伪代码为下,可以看到SGD、BGD、MBGD的区别就是m的数量的区别。

2、Momentum-SGD
????????Momentum-SGD就是在随机梯度下降的基础上,加上了上一步的梯度,可以加快梯度下降法的收敛速度,减少震荡。
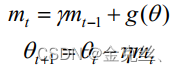
其中就是动量项,它累积了之前迭代时的梯度值,
是动量参数,位于0到1之间。相比于随机梯度下降,如果当前时刻求得的梯度方向和上一时刻的梯度方向相同,那么动量就会使相同方向的梯度不断累加,如果当前时刻求得的梯度方向和上一时刻的梯度方向不相同,那么不同方向的梯度则相互抵消,因而可以一定程度上克服“Z”字形的振荡迭代,更快到达最优点,Momentum-SGD伪代码为下:? ? ? ?

?3、NAG(Nesterov Accelerated Gradient,NAG)
????????NAG是在SGD、Momentum-SGD的基础上的进一步改进。我们知道在时刻t的主要下降方向是由累积动量决定的,因为动量系数通常为0.9以上,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果先跟着累积动量走了一步,那个时候再怎么走。因此,NAG先不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向。然后用下一个点的梯度方向,与历史累积动量相结合,再计算当前时刻的累积动量。
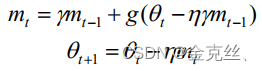
其中就是先跟着上一步累积的动量走一步,再去计算当前时刻的累积动量,然后再走一步。
4、Adagrad
?????????Adagrad是一种自适应的梯度下降法,它能够针对参数更新的频率调整它们的更新幅度——对于更新频繁且更新量大的参数,适当减小他们的步长;对于更新不频繁的参数,适当增大它们的步长。这种方法的思想很适合一些数据分布不均匀的任务。
未完待续。