[人工智能]【图像分割】2021-SegFormer NeurIPS

【图像分割】2021-SegFormer NeurIPS

论文题目: SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers

论文地址:https://arxiv.org/abs/2105.15203v3

代码地址: https://github.com/NVlabs/SegFormer

论文团队：香港大学, 南京大学, NVIDIA, Caltech

SegFormer论文详解，2021CVPR收录，将Transformer与语义分割相结合的作品，

1. 简介

1.1 简介

• 2021可以说是分割算法爆发的一年，首先ViT通过引入transform将ADE20K mIOU精度第一次刷到50%，超过了之前HRnet+OCR效果，
• 然后再是Swin屠榜各大视觉任务，在分类，语义分割和实例分割都做到了SOTA，斩获ICCV2021的bset paper，
• 然后Segformer有凭借对transform再次深层次优化，在拿到更高精度的基础之上还大大提升了模型的实时性。

动机来源有：SETR中使用VIT作为backbone提取的特征较为单一，PE限制预测的多样性，传统CNN的Decoder来恢复特征过程较为复杂。主要提出多层次的Transformer-Encoder和MLP-Decoder，性能达到SOTA。

1.2 解决的问题

SegFormer是一个将transformer与轻量级多层感知器(MLP)解码器统一起来的语义分割框架。SegFormer的优势在于：

1. SegFormer设计了一个新颖的分级结构transformer编码器，输出多尺度特征。它不需要位置编码，从而避免了位置编码的插值（当测试分辨率与训练分辨率不同时，会导致性能下降）。
2. SegFormer避免了复杂的解码器。提出的MLP解码器从不同的层聚合信息，从而结合局部关注和全局关注来呈现强大的表示。作者展示了这种简单和轻量级的设计是有效分割transformer的关键。

2. 网络

2.1 架构

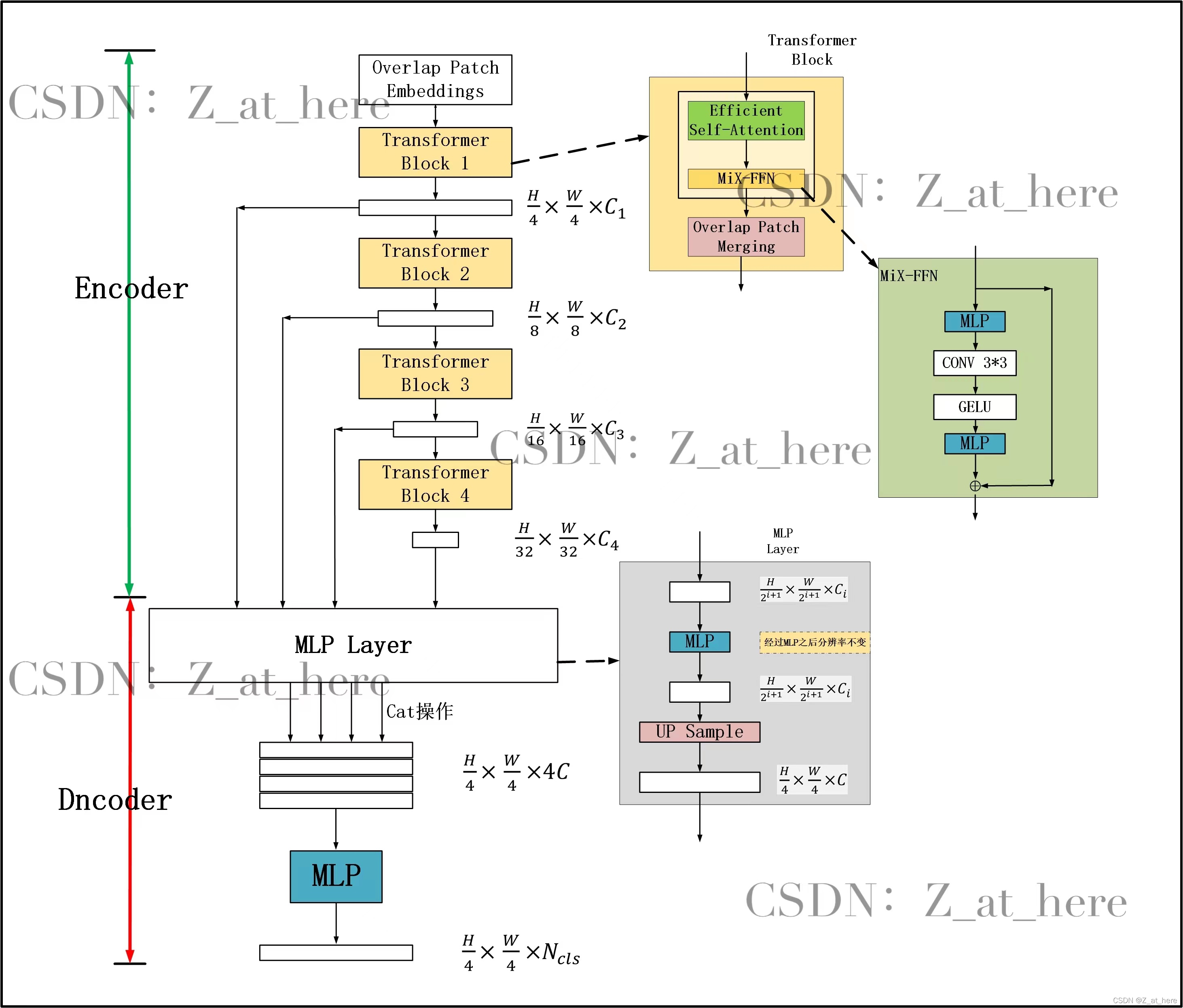
1) 总体结构

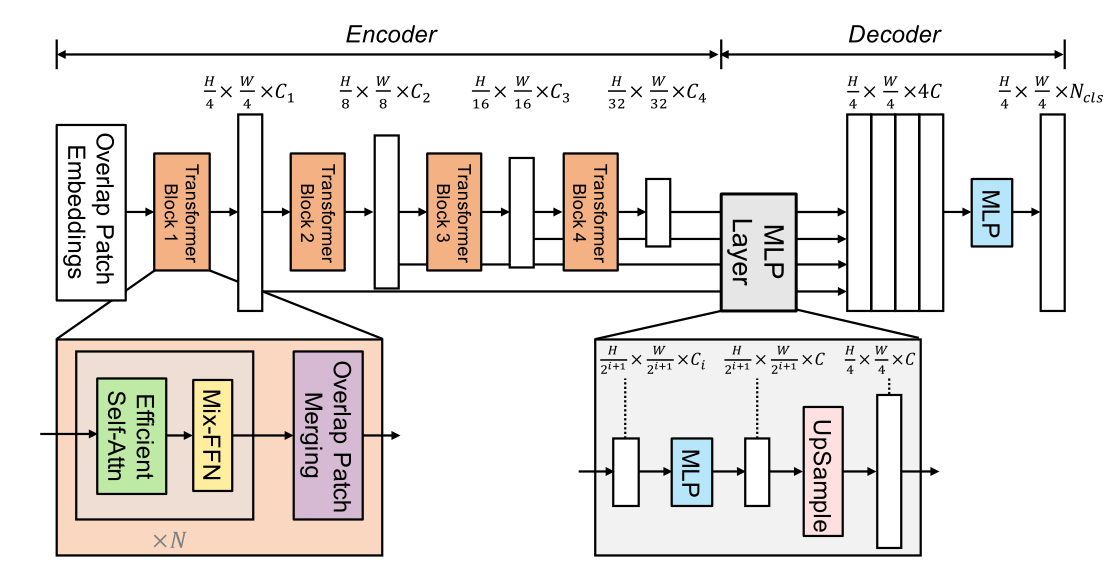
这种架构类似于ResNet,Swin-Transformer。经过一个阶段，

• 编码器：一个分层的Transformer编码器，用于生成高分辨率的粗特征和低分辨率的细特征

  由Transformer blocks*N 组成一个单独的阶段(stage)。

  一个Transformer block 由3个部分组成

  • Overlap Patch Merging
  • Mix-FFN
  • Effcient Self-Atten

• 解码器：一个轻量级的All-MLP解码器，融合这些多级特征，产生最终的语义分割掩码。

2) 编码器配置

下面是SegFormer的编码器的具体配置

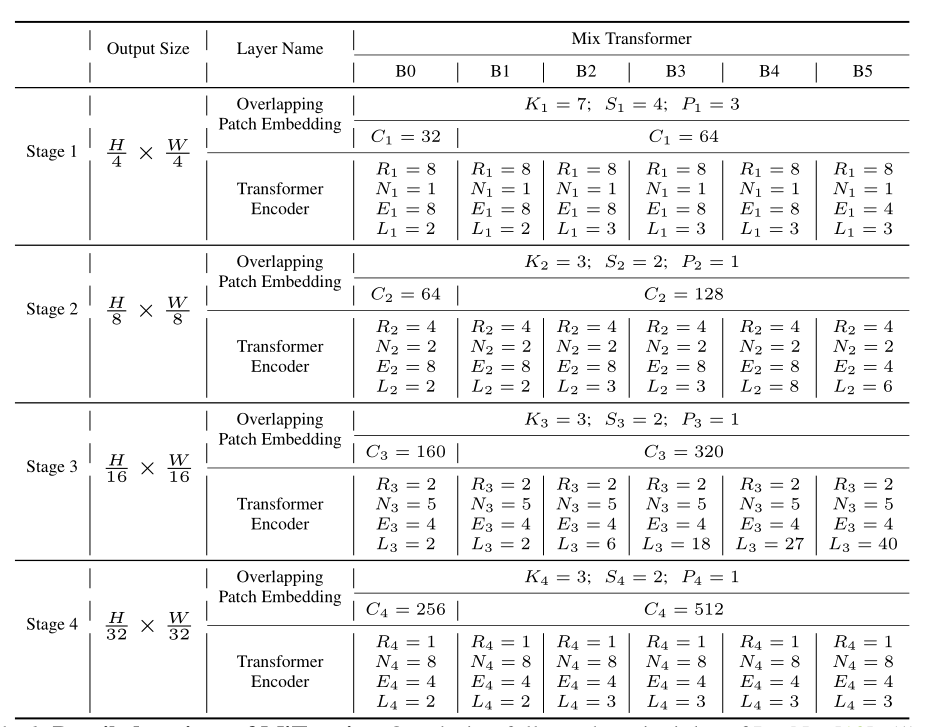
3) 分层结构

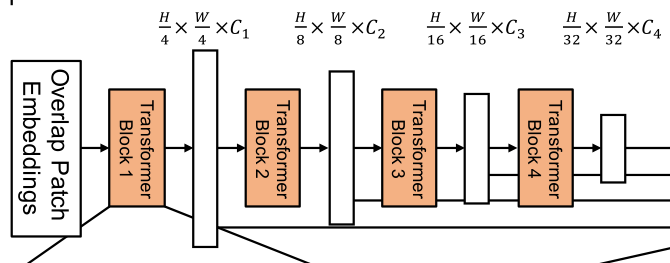
与只能生成单分辨率特征图的ViT不同，该模块的目标是对给定输入图像生成类似cnn的多级特征。这些特征提供了高分辨率的粗特征和低分辨率的细粒度特征，通常可以提高语义分割的性能。

更准确地说，给定一个分辨率为$H\times W\times 3$。我们进行patch合并，得到一个分辨率为$(\frac{H}{2^{i+1}}\times \frac{W}{2^{i+1}}\times C)$的层次特征图$F_i$,其中 i ∈ { 1 , 2 , 3 , 4 } i\in\{1,2,3,4\} i∈{1,2,3,4}。

举个例子，经过一个阶段$F_1=(\frac{H}{4}\times \frac{W}{4}\times C)\to F_2=(\frac{H}{8}\times \frac{W}{8}\times C)$

2.2 分层的Transformer解码器

编码器由3个部分组成，首先讲一下，下采样模块

1) Overlap Patch Merging

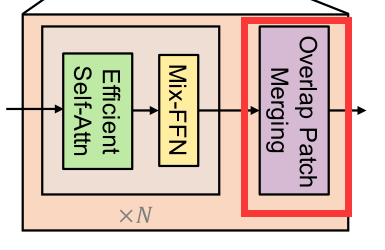
对于一个映像patch，ViT中使用的patch合并过程将一个$N\times N\times 3$的图像统一成$1\times 1\times C$向量。这可以很容易地扩展到将一个$2\times 2\times C_i$特征路径统一到一个$1\times 1\times C_{i+1}$向量中，以获得分层特征映射。

使用此方法，可以将层次结构特性从$F_1=(\frac{H}{4}\times \frac{W}{4}\times C)\to F_2=(\frac{H}{8}\times \frac{W}{8}\times C)$。然后迭代层次结构中的任何其他特性映射。这个过程最初的设计是为了结合不重叠的图像或特征块。因此，它不能保持这些斑块周围的局部连续性。相反，我们使用重叠补丁合并过程。因此，论文作者分别通过设置K，S，P为（7，4，3）（3，2，1）的卷积来进行重叠的Patch merging。其中，K为kernel，S为Stride，P为padding。

说的这么花里胡哨的，其实作用就是和MaxPooling一样，起到下采样的效果。使得特征图变成原来的$\frac{1}{2}$

2) Efficient Self-Attention

编码器的主要计算瓶颈是自注意层。在原来的多头自注意过程中，每个头$K,Q,V$都有相同的维数$N\times C$,其中$N=H\times W$为序列的长度，估计自注意为：
$$Attention(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{d_{head}}})V$$
这个过程的计算复杂度是$O(N^2)$,这对于大分辨率的图像来说是巨大的。

论文作者认为，网络的计算量主要体现在自注意力机制层上。为了降低网路整体的计算复杂度，论文作者在自注意力机制的基础上，添加的缩放因子$R$，来降低每一个自注意力机制模块的计算复杂度。
$$\begin{array}{rl}\hat{K}& =Reshape(\frac{N}{R},C?R)(K)\\ K& =Linear(C?R,C)(\hat{K})\end{array}$$
其中第一步将$K$的形状由$N\times C$转变为$\frac{N}{R}\times (C?R)$，

第二步又将$K$的形状由$\frac{N}{R}\times (C?R)$转变为$\frac{N}{R}\times C$。因此，计算复杂度就由$O(N^2)$降至$O(\frac{N^2}{R})$。在作者给出的参数中，阶段1到阶段4的$R$分别为$[64,16,4,1]$

3) Mix-FFN

VIT使用位置编码PE（Position Encoder）来插入位置信息，但是插入的PE的分辨率是固定的，这就导致如果训练图像和测试图像分辨率不同的话，需要对PE进行插值操作，这会导致精度下降。

为了解决这个问题CPVT（Conditional positional encodings for vision transformers. arXiv, 2021）使用了3X3的卷积和PE一起实现了data-driver PE。

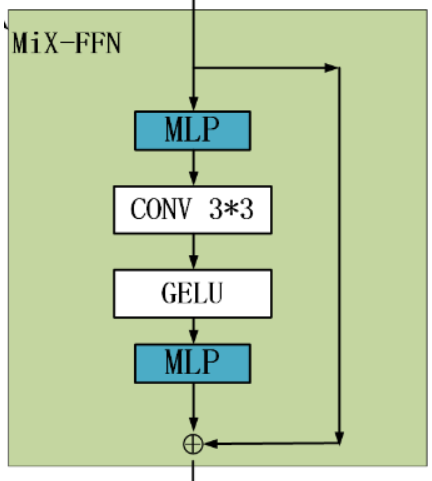
引入了一个 Mix-FFN，考虑了padding对位置信息的影响，直接在 FFN （feed-forward network）中使用 一个3x3 的卷积，MiX-FFN可以表示如下：
$$X_{out}=MLP(GELU(Con{v}_{3\times 3}(MLP(X_{in}))))+X_{in}$$
其中$X_{in}$是从self-attention中输出的feature。Mix-FFN混合了一个$3?3$的卷积和MLP在每一个FFN中。即根据上式可以知道MiX-FFN的顺序为：输入经过MLP，再使用$Con{v}_{3\times 3}$操作，正在经过一个GELU激活函数，再通过MLP操作，最后将输出和原始输入值进行叠加操作，作为MiX-FFN的总输出。

在实验中作者展示了$3?3$的卷积可以为transformer提供PE。作者还是用了深度可以分离卷积提高效率，减少参数。

2.3 轻量级MLP解码器

SegFormer集成了一个轻量级解码器，只包含MLP层。实现这种简单解码器的关键是，SegFormer的分级Transformer编码器比传统CNN编码器具有更大的有效接受域(ERF)。

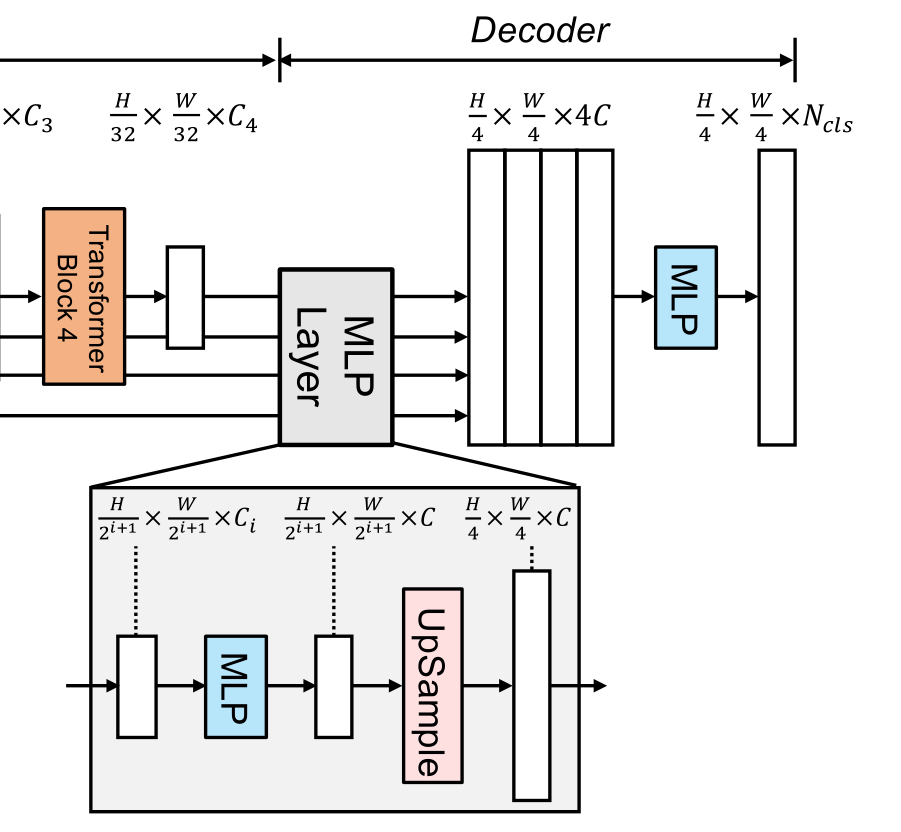
SegFormer所提出的全mlp译码器由四个主要步骤组成。

1. 来自MiT编码器的多级特性通过MLP层来统一通道维度。
2. 特征被上采样到1/4并连接在一起。
3. 采用MLP层融合级联特征$F$
4. 另一个MLP层采用融合的$\frac{H}{4}\times \frac{W}{4}\times N_{cls}$分辨率特征来预测分割掩码$M$,其中表示类别数目

解码器可以表述为：

$$\begin{array}{rl}{\hat{F}}_i& =Linear(C_i,C)(F_i),?i\\ {\hat{F}}_i& =Upsample(\frac{W}{4}\times \frac{W}{4})({\hat{F}}_i),?i\\ F& =Linear(4C,C)(Concat({\hat{F}}_i)),?i\\ M& =Linear(C,N_{cls})(F)\end{array}$$

2.4 有效接受视野(ERF)

这个部分是 用来证明 解码器是非常有效的

对于语义分割，保持较大的接受域以包含上下文信息一直是一个中心问题。SegFormer使用有效接受域(ERF)作为一个工具包来可视化和解释为什么All-MLP译码器设计在TransFormer上如此有效。在下图中可视化了DeepLabv3+和SegFormer的四个编码器阶段和解码器头的ERF：

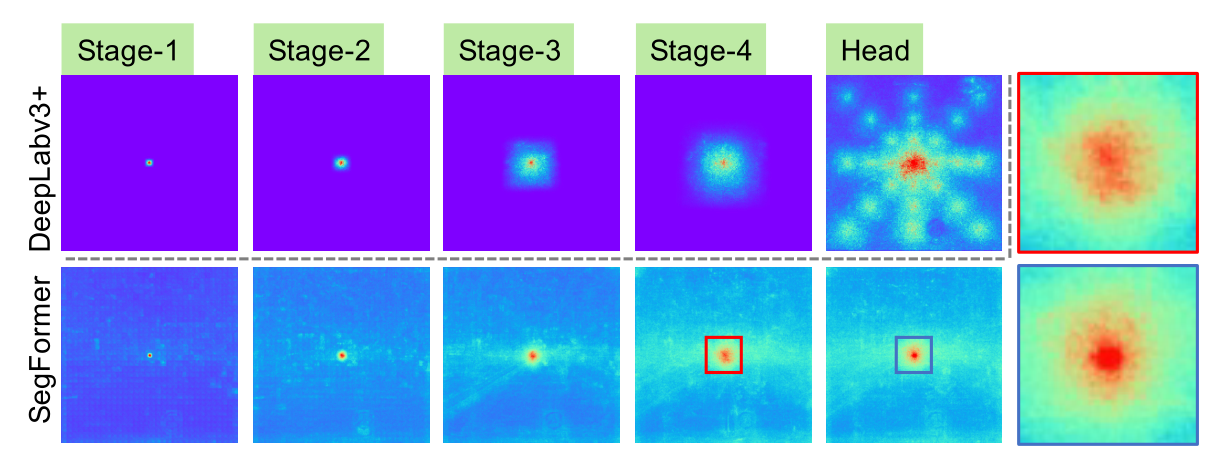
从上图中可以观察到：

1. DeepLabv3+的ERF即使在最深层的Stage4也相对较小。
2. SegFormer编码器自然产生局部注意，类似于较低阶段的卷积，同时能够输出高度非局部注意，有效捕获Stage4的上下文。
3. 如放大Patch所示，MLP头部的ERF(蓝框)与Stage4(红框)不同，其非局部注意力和局部注意力显著增强。

CNN的接受域有限，需要借助语境模块扩大接受域，但不可避免地使网络变复杂。All-MLP译码器设计得益于transformer中的非局部注意力，并在不复杂的情况下导致更大的接受域。然而，同样的译码器设计在CNN主干上并不能很好地工作，因为整体的接受域是在Stage4的有限域的上限。

更重要的是，All-MLP译码器设计本质上利用了Transformer诱导的特性，同时产生高度局部和非局部关注。通过统一它们，All-MLP译码器通过添加一些参数来呈现互补和强大的表示。这是推动我们设计的另一个关键原因。

3. 代码

下面展示的SegFormer 的Bo版本。其他版本，可以自己调整

from math import sqrt
from functools import partial
import torch
from torch import nn, einsum
import torch.nn.functional as F

from einops import rearrange, reduce
from einops.layers.torch import Rearrange


# helpers

def exists(val):
    return val is not None


def cast_tuple(val, depth):
    return val if isinstance(val, tuple) else (val,) * depth


# classes

class DsConv2d(nn.Module):
    def __init__(self, dim_in, dim_out, kernel_size, padding, stride=1, bias=True):
        super().__init__()
        self.net = nn.Sequential(
            nn.Conv2d(dim_in, dim_in, kernel_size=kernel_size, padding=padding, groups=dim_in, stride=stride,
                      bias=bias),
            nn.Conv2d(dim_in, dim_out, kernel_size=1, bias=bias)
        )

    def forward(self, x):
        return self.net(x)


class LayerNorm(nn.Module):
    def __init__(self, dim, eps=1e-5):
        super().__init__()
        self.eps = eps
        self.g = nn.Parameter(torch.ones(1, dim, 1, 1))
        self.b = nn.Parameter(torch.zeros(1, dim, 1, 1))

    def forward(self, x):
        std = torch.var(x, dim=1, unbiased=False, keepdim=True).sqrt()
        mean = torch.mean(x, dim=1, keepdim=True)
        return (x - mean) / (std + self.eps) * self.g + self.b


class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.fn = fn
        self.norm = LayerNorm(dim)

    def forward(self, x):
        return self.fn(self.norm(x))


class EfficientSelfAttention(nn.Module):
    def __init__(
            self,
            *,
            dim,
            heads,
            reduction_ratio
    ):
        """
        自注意力层
        Args:
            dim: 输入维度
            heads: 注意力头数
            reduction_ratio: 缩放因子
        """
        super().__init__()
        self.scale = (dim // heads) ** -0.5
        self.heads = heads

        self.to_q = nn.Conv2d(dim, dim, 1, bias=False)
        self.to_kv = nn.Conv2d(dim, dim * 2, reduction_ratio, stride=reduction_ratio, bias=False)
        self.to_out = nn.Conv2d(dim, dim, 1, bias=False)

    def forward(self, x):
        h, w = x.shape[-2:]
        heads = self.heads

        q, k, v = (self.to_q(x), *self.to_kv(x).chunk(2, dim=1))
        q, k, v = map(lambda t: rearrange(t, 'b (h c) x y -> (b h) (x y) c', h=heads), (q, k, v))

        sim = einsum('b i d, b j d -> b i j', q, k) * self.scale
        attn = sim.softmax(dim=-1)

        out = einsum('b i j, b j d -> b i d', attn, v)
        out = rearrange(out, '(b h) (x y) c -> b (h c) x y', h=heads, x=h, y=w)
        return self.to_out(out)


class MixFeedForward(nn.Module):
    def __init__(
            self,
            *,
            dim,
            expansion_factor
    ):
        super().__init__()
        hidden_dim = dim * expansion_factor
        self.net = nn.Sequential(
            nn.Conv2d(dim, hidden_dim, 1),
            DsConv2d(hidden_dim, hidden_dim, 3, padding=1),
            nn.GELU(),
            nn.Conv2d(hidden_dim, dim, 1)
        )

    def forward(self, x):
        return self.net(x)


class MiT(nn.Module):

    def __init__(
            self,
            *,
            channels,
            dims,
            heads,
            ff_expansion,
            reduction_ratio,
            num_layers
    ):
        """
        Mix Transformer Encoder
        Args:
            channels:
            dims:
            heads:
            ff_expansion:
            reduction_ratio:
            num_layers:
        """
        super().__init__()
        stage_kernel_stride_pad = ((7, 4, 3), (3, 2, 1), (3, 2, 1), (3, 2, 1))

        dims = (channels, *dims)
        dim_pairs = list(zip(dims[:-1], dims[1:]))

        self.stages = nn.ModuleList([])

        for (dim_in, dim_out), (kernel, stride, padding), num_layers, ff_expansion, heads, reduction_ratio in \
                zip(dim_pairs, stage_kernel_stride_pad, num_layers, ff_expansion, heads, reduction_ratio):

            get_overlap_patches = nn.Unfold(kernel, stride=stride, padding=padding)
            overlap_patch_embed = nn.Conv2d(dim_in * kernel ** 2, dim_out, 1)

            layers = nn.ModuleList([])

            for _ in range(num_layers):
                layers.append(nn.ModuleList([
                    PreNorm(dim_out, EfficientSelfAttention(dim=dim_out,
                                                            heads=heads,
                                                            reduction_ratio=reduction_ratio)),
                    PreNorm(dim_out, MixFeedForward(dim=dim_out, expansion_factor=ff_expansion)),
                ]))

            self.stages.append(nn.ModuleList([
                get_overlap_patches,
                overlap_patch_embed,
                layers
            ]))

    def forward(self, x, return_layer_outputs=False):
        # 宽，高
        h, w = x.shape[-2:]

        layer_outputs = []
        for (get_overlap_patches, overlap_embed, layers) in self.stages:

            x = get_overlap_patches(x)

            num_patches = x.shape[-1]
            ratio = int(sqrt((h * w) / num_patches))
            x = rearrange(x, 'b c (h w) -> b c h w', h=h // ratio)
            x = overlap_embed(x)

            # 开始计算
            for (attn, ff) in layers:
                x = attn(x) + x
                x = ff(x) + x

            layer_outputs.append(x)

        ret = x if not return_layer_outputs else layer_outputs
        return ret


class Segformer(nn.Module):
    def __init__(
            self,
            *,
            dims=(32, 64, 160, 256),
            heads=(1, 2, 5, 8),
            ff_expansion=(8, 8, 4, 4),
            reduction_ratio=(8, 4, 2, 1),
            num_layers=2,
            channels=3,
            decoder_dim=256,
            num_classes=19
    ):
        """
        Args:
            dims: 4个阶段，出来的通道数
            heads: 每个阶段，使用的注意力头数目
            ff_expansion: mix-ffn 中 3*3卷积的扩张倍率
            reduction_ratio: 自注意力层缩放因子
            num_layers: 每个transformer blocks块重复的次数
            channels: 输入通道数，一般为3
            decoder_dim: 解码器维度 。 作用: 编码器的特征图统一 上采样--> decoder_dim 维度
            num_classes: 分类数目
        """
        super().__init__()
        # 该函数作用就是，如果是数字，就复制4分，变成tuple。比如 2-->(2,2,2,2)
        dims, heads, ff_expansion, reduction_ratio, num_layers = map(partial(cast_tuple, depth=4),
                                                                     (dims, heads, ff_expansion, reduction_ratio,
                                                                      num_layers))
        assert all([*map(lambda t: len(t) == 4, (dims, heads, ff_expansion, reduction_ratio,
                                                 num_layers))]), 'only four stages are allowed, all keyword arguments must be either a single value or a tuple of 4 values'

        self.mit = MiT(
            channels=channels,
            dims=dims,
            heads=heads,
            ff_expansion=ff_expansion,
            reduction_ratio=reduction_ratio,
            num_layers=num_layers
        )

        self.to_fused = nn.ModuleList([nn.Sequential(
            nn.Conv2d(dim, decoder_dim, 1),
            nn.Upsample(scale_factor=2 ** (i))
        ) for i, dim in enumerate(dims)])

        self.to_segmentation = nn.Sequential(
            nn.Conv2d(4 * decoder_dim, decoder_dim, 1),
            nn.Conv2d(decoder_dim, num_classes, 1),
        )

    def forward(self, x):
        # 返回的4个特征值，分别的1/4 ,1/8, 1/16, 1/32
        layer_outputs = self.mit(x, return_layer_outputs=True)
        """
        torch.Size([1, 32, 56, 56])
        torch.Size([1, 64, 28, 28])
        torch.Size([1, 160, 14, 14])
        torch.Size([1, 256, 7, 7])
        """
        # 这里进行上采样的
        fused = [to_fused(output) for output, to_fused in zip(layer_outputs, self.to_fused)]

        # print(len(fused))
        # print(fused[0].shape)
        fused = torch.cat(fused, dim=1)
        fused = self.to_segmentation(fused)

        # 直接而对1/4 的特征图。进行上采样
        return F.interpolate(fused, size=x.shape[2:], mode='bilinear', align_corners=False)


if __name__ == '__main__':
    x = torch.randn(size=(1, 3, 224, 224))
    model = Segformer()
    print(model)
    from thop import profile

    input = torch.randn(1, 3, 224, 224)
    flops, params = profile(model, inputs=(input,))
    print("flops:{:.3f}G".format(flops / 1e9))
    print("params:{:.3f}M".format(params / 1e6))
    # y = model(x)
    # print(y.shape)

参考资料

https://blog.csdn.net/weixin_43610114/article/details/125000614

https://blog.csdn.net/weixin_44579633/article/details/121081763

https://blog.csdn.net/qq_39333636/article/details/124334384

语义分割之SegFormer分享_xuzz_498100208的博客-CSDN博客

论文笔记——Segformer: 一种基于Transformer的语义分割方法 - 知乎 (zhihu.com)

手把手教你使用Segformer训练自己的数据_中科哥哥的博客-CSDN博客