论文地址:Going deeper with convolutions
随着在AI方面新的论文的发表,可以看出神经网络的发展,越来越往人脑结构的方向在研究,从最开始的感知器到全连接层结构(稠密结构),再到卷积神经网络(稀疏结构),尤其是随着网络越来越深和复杂,将更加凸显稀疏结构的优势,为什么呢,因为人脑的神经元之间的连接就是一种稀疏的结构,类似于赫布理论。其中“neurons that fire together, wire together”神经元一起激活(放电),一起连接,这个很有意思,也就是说,大脑的神经元是依靠放电来传递信号,如果不同神经元经常性同时放电,那么它们之间的连接就会越紧密。
论文中模型的设计遵循了实践直觉,即视觉信息应该在不同的尺度上处理然后聚合,为的是下一阶段可以从不同尺度同时抽象特征。结论也指出了通过易获得的密集构造块来近似期望的最优稀疏结果是改善计算机视觉神经网络的一种可行方法,也就是GoogLeNet“含并行连结的网络”模型的意义,因为这样的一种全新思想打破了以往的串联加深层的做法,往更稀疏的方向发展,我觉得这才是这篇paper最重要的价值。
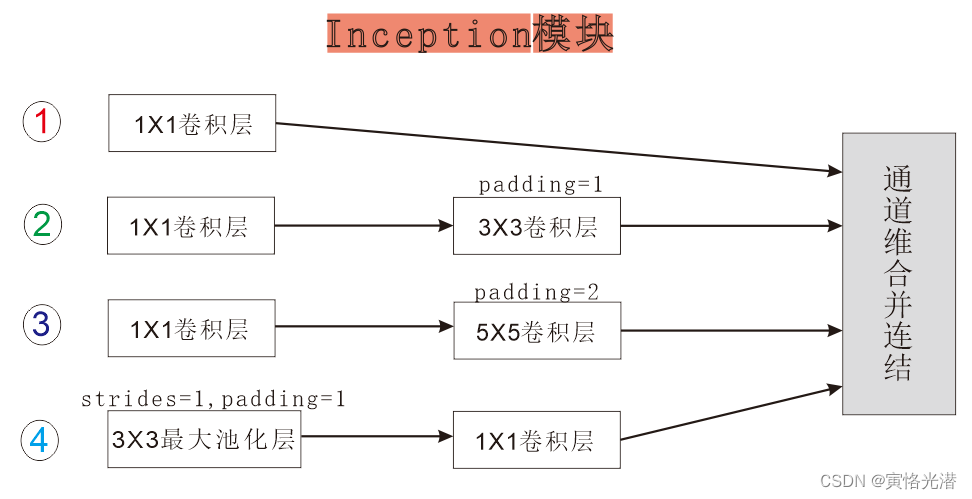
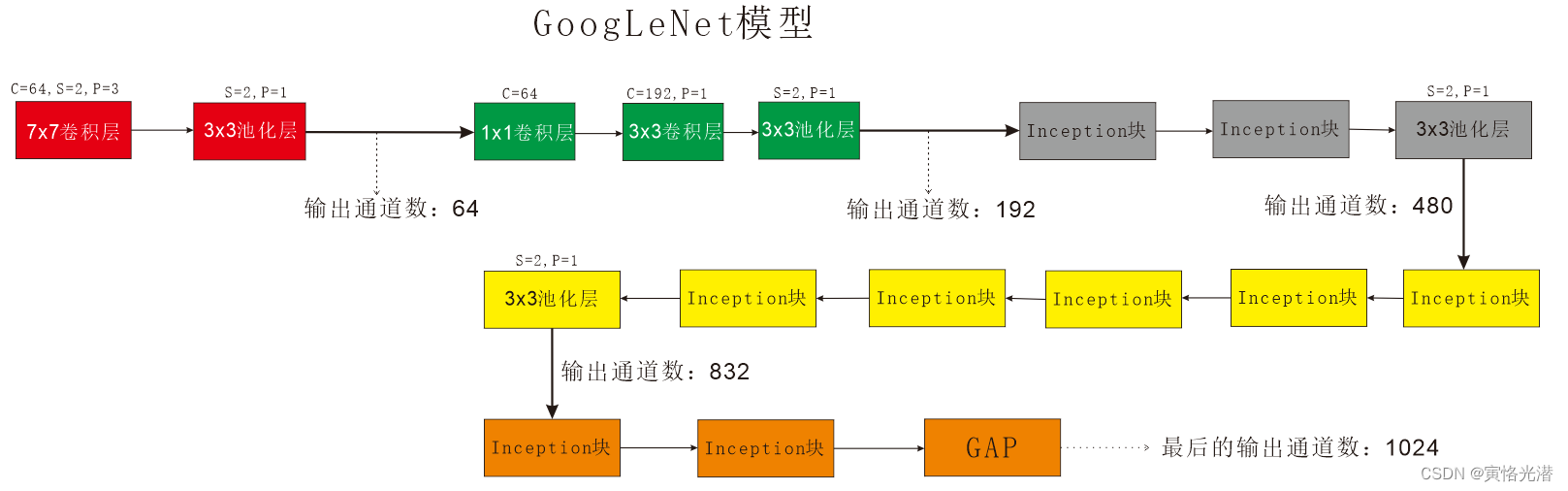
我们先来看两张图片,直观感受下,一张Inception模块,另一张就是GoogLeNet模型,由于GoogLeNet模型的层数比较深,避免图片尺寸太大,注意看我画箭头指向的方向以及使用颜色区分的模块。
?
Inception模块
上面图片可以看出,核心部分就是Inception模块,里面有4组并行的线路组成,代码实现如下:
import d2lzh as d2l
from mxnet import gluon,init,nd
from mxnet.gluon import nn
#四条并行的线路,然后在通道维进行连结
class Inception(nn.Block):
def __init__(self,c1,c2,c3,c4,**kwargs):
super(Inception,self).__init__(**kwargs)
#线路1
self.p1=nn.Conv2D(c1,kernel_size=1,activation='relu')
#线路2
self.p2_1=nn.Conv2D(c2[0],kernel_size=1,activation='relu')
self.p2_2=nn.Conv2D(c2[1],kernel_size=3,padding=1,activation='relu')
#线路3
self.p3_1=nn.Conv2D(c3[0],kernel_size=1,activation='relu')
self.p3_2=nn.Conv2D(c3[1],kernel_size=5,padding=2,activation='relu')
#线路4
self.p4_1=nn.MaxPool2D(pool_size=3,strides=1,padding=1)
self.p4_2=nn.Conv2D(c4,kernel_size=1,activation='relu')
def forward(self,x):
p1=self.p1(x)
p2=self.p2_2(self.p2_1(x))
p3=self.p3_2(self.p3_1(x))
p4=self.p4_2(self.p4_1(x))
return nd.concat(p1,p2,p3,p4,dim=1)#通道维进行连结构建GoogLeNet整个模型
#五大模块
B1=nn.Sequential()
B1.add(nn.Conv2D(64,kernel_size=7,strides=2,padding=3,activation='relu'),
nn.MaxPool2D(pool_size=3,strides=2,padding=1))
B2=nn.Sequential()
B2.add(nn.Conv2D(64,kernel_size=1,activation='relu'),
nn.Conv2D(192,kernel_size=3,padding=1,activation='relu'),
nn.MaxPool2D(pool_size=3,strides=2,padding=1))
B3=nn.Sequential()
B3.add(Inception(64,(96,128),(16,32),32),
Inception(128,(128,192),(32,96),64),#输出通道数128+192+96+64=480
nn.MaxPool2D(pool_size=3,strides=2,padding=1))
B4=nn.Sequential()
B4.add(Inception(192,(96,208),(16,48),64),
Inception(160,(112,224),(24,64),64),
Inception(128,(128,256),(24,64),64),
Inception(112,(144,288),(32,64),64),
Inception(256,(160,320),(32,128),128),
nn.MaxPool2D(pool_size=3,strides=2,padding=1))
B5=nn.Sequential()
B5.add(Inception(256,(160,320),(32,128),(128)),
Inception(384,(192,384),(48,128),128),
nn.GlobalAvgPool2D())
net=nn.Sequential()
net.add(B1,B2,B3,B4,B5,nn.Dense(10))
#查看各层输出形状
X=nd.random.uniform(shape=(1,1,96,96))
net.initialize()
for layer in net:
X=layer(X)
print(layer.name,'输出形状:',X.shape)
'''
sequential0 输出形状: (1, 64, 24, 24)
sequential1 输出形状: (1, 192, 12, 12)
sequential2 输出形状: (1, 480, 6, 6)
sequential3 输出形状: (1, 832, 3, 3)
sequential4 输出形状: (1, 1024, 1, 1)
dense0 输出形状: (1, 10)
'''训练模型
受限于GPU,还是以Fashion-MNIST数据集为例,注意的是关注这个网络模型的新特性才是学习的重点。
lr,num_epochs,batch_size,ctx=0.1,5,128,d2l.try_gpu()
net.initialize(force_reinit=True,ctx=ctx,init=init.Xavier())
trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':lr})
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size,resize=96)
d2l.train_ch5(net,train_iter,test_iter,batch_size,trainer,ctx,num_epochs)
'''
epoch 1, loss 2.1157, train acc 0.210, test acc 0.511, time 154.6 sec
epoch 2, loss 0.8424, train acc 0.666, test acc 0.782, time 143.6 sec
epoch 3, loss 0.5345, train acc 0.802, test acc 0.847, time 143.9 sec
epoch 4, loss 0.4107, train acc 0.846, test acc 0.870, time 144.0 sec
epoch 5, loss 0.3557, train acc 0.865, test acc 0.875, time 142.4 sec
'''