[人工智能]动手学深度学习---从全连接层到卷积层篇

卷积神经网络

1.从全连接层到卷积层

前言：MLP适合处理表格数据，行对应样本，列对应特征。但对于高维感知数据，就会变得不实用

（数据量过于庞大，需要大量GPU和耐心）

采用卷积神经网路(convolutional neural networks,CNN)时机器学习利用自然图像中一些已知结构的创造性方法

• 不变性

不变性意味着即使目标的外观发生了某种变化，但是你依然可以把它识别出来。这对图像分类来说是一种很好的特性，因为我们希望图像中目标无论是被平移，被旋转，还是被缩放，甚至是不同的光照条件、视角，都可以被成功地识别出来。

所以上面的描述就对应着各种不变性：

• 平移不变性：Translation Invariance
• 旋转/视角不变性：Ratation/Viewpoint Invariance
• 尺度不变性：Size Invariance
• 光照不变性：Illumination Invariance

①平移不变性

比如对图像分类任务来说，图像中的目标不管被移动到图片的哪个位置，得到的结果（标签）应该是相同的，这就是卷积神经网络中的平移不变性。

②局部性

神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终聚合这些局部特征，以在整个图像级别进行预测。

• 多层感知机的限制

这里的数学运算我存在问题，后续补充

2.图像卷积

前言：上一节我们解析了卷积层的数学原理，现在我们来看看它的实际应用

• 互相换运算

#####################################

严格来说卷积只是一种称谓，他所表达的运算实际是互相关运算(cross-correlation)。

#####################################

#这句话可能有错

所谓cross-correlation 实际是输入tensor与核tensor通过互相关运算产生输出张量，下面我们通过图解来解释cross-correlation

我们暂时忽略channel(第三维)情况，看看如何处理二维图像数据和隐藏表示(即经过cross-correlation得到的输出)

在二维的 cross-correlation中，卷积窗口从输入tensor的左上角开始，从左到右、从上到下。每当卷积窗口到达新位置时，在窗口内的tensor与卷积核tensor进行按元素相乘再相加得到隐藏表示的单一标量像素值。如上述例子，互相关运算如下：

注意， 卷积核只与图像中每个大小完全适合的位置进行互相关运算，不满足则继续滑动直到满足位置 输出tensor窗口大小公式如下：(n 为输入的tensor，k为卷积核)

接下来，我们在corr2d函数中用代码实现上述卷积操作：

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X,K):
    """计算二维互相关运算"""
    h,w=K.shape   #得到卷积核(kernel)的行长、宽长
    #创建一个与隐藏表示同样形状的全为0的tensor
    Y=torch.zeros((X.shape[0]-K.shape[0]+1,X.shape[1]-K.shape[1]+1))
    
    for i in range(Y.shape[0]):
    	for j in range(Y.shape[1]):
            #按元素重新一个个填充
            Y[i,j]=(X[i:i+h,j:j+w]*K).sum() #得到进行互相关运算后的隐藏表示，步长为1
    return Y
        	

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)

result：

tensor([[19., 25.],
        [37., 43.]])

• 卷积层

卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。 所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。 就像我们之前随机初始化全连接层一样，在训练基于卷积层的模型时，我们也随机初始化卷积核权重。

基于上面定义的corr2d函数实现二维卷积层。在__init__构造函数中，将weight和bias声明为两个模型参数。前向传播函数调用corr2d函数并添加偏置。

class Conv2D(nn.module):
    def __init__(self,kernel_size):#kernel_size为卷积核的shape
        super().__init__()
        
        #weight为Conv2D的属性，self.weight是Paramter类的实例
        self.weight=nn.Parameter(torch.rand(kernel_size))#初始化卷积核权重
        self.bias=nn.Parameter(torch.zeros(1))
        
    def forword(self,X):
        return corr2d(X,self.weight)+self.bias #广播机制

高度和宽度分别为h和w的卷积核可以被称为h×w卷积或h×w卷积核。 我们也将带有h×w卷积核的卷积层称为h×w卷积层。

• 图像中目标的边缘检测

如下是卷积层的一个简单应用：通过找到像素变化的位置，来检测图像中不同颜色的边缘。 首先，我们构造一个6×8像素的黑白图像。中间四列为黑色（0），其余像素为白色（1）。

X=torch.ones((6,8))
X[:,2:6]=0
X

result:
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])

接下来，我们构造h=1，w=2的卷积核K。

当进行互相关运算时，如果水平相邻的两元素相同，则输出为零，否则输出为非零。

K = torch.tensor([[1.0, -1.0]])

现在，我们对参数X（输入）和K（卷积核）执行互相关运算。 如下所示，输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘，其他情况的输出为0。

Y = corr2d(X, K)
Y

result：
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

现在我们将输入的二维图像转置，再进行如上的互相关运算。 其输出如下，之前检测到的垂直边缘消失了。 不出所料，这个卷积核K只可以检测垂直边缘，无法检测水平边缘。

corr2d(X.t(), K)

result：
tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])

• 学习卷积核

当有更复杂的情况时，我们不可能手动设计滤波器，那么我们是否可以学习由X生成Y的卷积核呢？

下面，我们首先构造一个卷积层(具有卷积核weight，bias，forword函数等)，并将卷积核初始化为随机tensor。接下来我，在每个epoch中，我们比较Y与卷积层的输出的平方误差，然后据此计算gradient来更新卷积核。为简单起见，我们直接采取内置的二维卷积层，并忽略bias

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
#最前面的1,1为in_channels,out_channels
# 这个二维卷积层使用四维输入和输出格式（输出通道、输入通道、高度、宽度），
# 其中批量大小和通道数都为1
conv2d=nn.Conv2d(1,1,kernel_size=(1,2),bias=False) 
X=X.reshape((1,1,6,8))
Y=Y.reshape((1,1,6,7))
lr=3e-2 #学习率

for i in range(10):#训练的基本不走
    y_hat=conv2d(X)
    l=(Y-y_hat)**2
    con2d.zero_grad()
    l,sum().backward()#损失函数求导，得到loss关于卷积核的导数
    #迭代卷积核，即卷积核(权重)更新
    conv2d.weight.data[:]-=lr*conv2d.weight.grad
    
    if (i+1)%2==0:
         print(f'epoch {i+1}, loss {l.sum():.3f}')

• 互相关与卷积

？？？因为前一小节未充分理解，所以难以阐述两者关系

• 特征映射和感受野

在卷积神经网络中，对于某一层的任意元素x，其感受野（receptive field）是指在前向传播期间可能影响x计算的所有元素（来自所有先前层）。

例： 让我们用互相关运算中的图为例来解释感受野： 给定2×2卷积核，阴影输出元素值19的感受野是输入阴影部分的四个元素。 假设之前输出为Y，其大小为2×2，现在我们在其后附加一个卷积层，该卷积层以Y为输入，输出单个元素z。 在这种情况下，Y上的z的感受野包括Y的所有四个元素，而输入的感受野包括最初所有九个输入元素。 因此，当一个特征图中的任意元素需要检测更广区域的输入特征时，我们可以构建一个更深的网络 （特征图不是卷积核，而是经过卷积操作得到的输出）

3.填充（paddle）和步幅 （stride）

卷积的输出形状取决于输入形状和卷积核的形状

那还有什么因素影响输出的shape呢？

①填充 padding

当应用了连续的卷积后，我们得到的输出远小于输入的shape，如此一来原始图像的边界丢失了许多有用信息，而padding是解决此问题最有效的方法。

在输入图像的边界填充元素(通常为0)，填充操作如下图所示：

通常，如果我们填充P_h行，则顶部与底部各填充 1/2 P_h行，填充 P_w列同理

填充后，输出公式如下：

这意味着输出的高度和宽度分别增加 P_h行和p_w列

通常，若要保持输入的shape与经过卷积后的输出的shape一致，则需设置p_h=K_h-1和p_w=K_w-1。

1. 若K_h为奇数，则在顶部与底部各填充 1/2 p_h行，k_w同理
2. 若K_h为偶数，则在顶部或者底部填充 1/2 p_h行，只需要填充一侧，k_w同理

卷积神经网络的卷积核(kernel)的高度和宽度通常为奇数。

好处：

1. 保持空间维度同时，可以同时在上下，左右填充相同数量的行(这里的相同数量指上下填充的行数相同，列数同理)
2. 提供书写便利

代码示例：

? 我们创建一个 高度和宽度为3的二维卷积层，并在所有侧边填充1个像素。给定高度和宽度为8的输入，则输出的高度和宽度也是8。 即k_h=h_w=3,p_h=p_w=2,p_h=k_h-1,p_w同理，所以输出shape不变

import torch 
from torch import nn




def comp_conv2d(conv2d,X):
    # 为了方便起见，我们定义了一个计算卷积层的函数。
	# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
    #此处为元组相加，X.shape=(8,8)
    #(1,1)+(8,8)=(1,1,8,8)
    # 这里的（1，1）表示批量大小和通道数都是1
    X=X.reshape((1,1)+X.shape)
    
	Y=conv2d(X)#得到经过卷积的Y
    return Y.reshape(Y.shape[2:])#将Y重新整合为2维矩阵并返回Y(因为这里的通道数，批量数为1，所以不影响)

# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d=nn.Conv2d(1,1,kernel_size=3,padding=1)
#conv2d的输入shape为(1,1,8,8),输出shape同样为(1,1,8,8)
X=torch.rand(size=(8,8))
cop_conv2d(conv2d,X).shape

result：
torch.Size([8, 8]) #表明输出的高宽为[8,8]

当kernel的高度与宽度不等时，可以填充不同的高度和宽度，使输出和输入具有相同的高度和宽度。 在如下示例中，我们使用高度为5，宽度为3的卷积核，高度和宽度两边的填充分别为2和1。

#padding为(2,1)，即高度和宽度两边的填充行数列数分别为2和1，即4，2
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))

comp_conv2d(conv2d, X).shape

result：
torch.Size([8, 8])

②步幅 stride （向下取整）

计算互相关时，卷积窗口默认从左上角开始，向下、向右滑动。 卷积层默认每次滑动一个元素。

卷积窗口也可以跳过中间位置，每次滑动多个元素。每次滑动元素的数量称为 步幅（stride）。

下图为指定步幅的输出形状公式：

下面为输出形状简化：

①如果设置 p_h=k_h-1 和 p_w=k_w-1.则输出形状简化为 [(n_h+s_h?1)/s_h]×[(n_w+s_w?1)/s_w]。

②更进一步，如果 输入的高度和宽度可以被垂直和水平步幅整除，则输出形状为状将为(n_h/s_h)×(n_w/s_w) (因为向下取整， （s_w-1）<1，则视为0)

下面，我们将高度和宽度的步幅设置为2，从而将输入的高度和宽度减半

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape

result:
torch.Size([4, 4])

接下来，看一个稍微复杂的例子

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape

result:
torch.Size([2, 2])

输入高度和宽度两侧的填充数量分别为p_h和p_w时，我们称之为填充(p_h,p_w)。当p_h=p_w=p时，填充是p。同理，步幅为**(s_h,s_w)。当步幅为s_h=s_w=s时，步幅为s**。默认情况下，填充为0，步幅为1。在实践中，我们很少使用不一致的步幅或填充，也就是说，我们通常有p_h=p_w和s_h=s_w。

小结: stride 和padding可用于有效调整数据的维度 (w,h)

• 多输入多输出通道

前言：在前面我们的例子中，进行互相关运算的始终是二维的数据与卷积核。而大多数图片数据通常为 3维tensor(具有 R G B 3通道)，shape为（3 X h X w）,我们将这个大小为3的轴称为 通道(channel) 维度

本节我们将深入研究具有多输入 和多输出的kernel

• 多输入通道

当输入包含多个channel时，需要构造 相同channel 数的 kernel，便与进行互相关运算。

多输入通道数据**(3维tensor)** 与 多输入通道 kernel (3维tensor) 是如何进行互相关运算的？

首先 我们在每个输入通道 进行 kernel(2维tensor） 与 输入 tensor (2维tensor) 进行互相关运算，最后将 每个输入通道上的结果进行求和 得到 最终的 2维 tensor。这就是多通道输入与多输入通道 kernel 之间进行二维互相关运算的结果

下图，我们进行 运算演示：

为加深理解，我们进行代码复现。

在此之前，我们回顾一下 zip()函数

#zip()函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个tuple，然后返回由这些tuple构成的list。如果各个迭代器的元素个数不一致，则返回的list长度与最短的list长度相同。同时，使用zip(*)号，可以将tuple解压为list

a='1111'
b='22222'
print(zip(a,b))
print(list(zip(a,b))
za,zb=zip(*zip(a,b))
print('za is {za},zb is {zb}'.format(za=za,zb=zb))

result:
    <zip object at 0x000001F9CFEC6E80>
    [('1','2'),('1','2'),('1','2'),('1','2')]#该结果证明了zip构成了元素为tuple的list
    za is ('1','1','1','1'), zb is('2','2','2','2')
    

多输入通道互相关运算 简而言之就是对每个输入通道执行2维的互相关操作，然后将结果相加

import torch
from d2l import torch as d2l

def corr2d_multi_in(X,K):
    # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
    #此处X，K为三维tensor  x,y 为具有高宽的2维tensor(x,y)为list中的tuple
    #sum 使得每个输入通道上的结果进行对应元素相加
    return sum(d2l.corr2d(x,k) for x,k in zip(X,K))

我们可以构造与 图6.4.1 中的值相对应的输入张量X和核张量K，以验证互相关运算的输出。

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

result：
tensor([[ 56.,  72.],
        [104., 120.]])

• 多输出通道

到目前为止，我们的kernel只有一个输出通道，即输出为单通道的2维tensor。用 c_i和c_o表示 输入和输出通道的数目，k_h和k_w为kernel的w和h。为获得多个channel的三维tensor ，我们在每个输出channel 创建一个形状为 c_i X k_h X k_w 的三维kernel tensor ，相当于 卷积核的shape 为 c_o X c_i X k_h X k_w（四维）。

在互相关运算中，每个输出通道先获取所有输入通道，再以对应该输出通道的三维 kernel 进行 多输入通道的计算，最后将多个2维tensor 进行某维度的连结形成新的3维tensor

def corr2d_multi_in_out(X,K):
    #此时K为四维tensor，第0维为输出通道
    return torch.stack([corr2d_multi_in(X,k) for k in K],0)
#解析：
#在每个输出通道上取出三维tensor-kernel然后进行 多输入通道计算,即在每个输入通道进行2维kernel与2维输入tensor进行互相关运算，最后用torch.stack(……,0)在第0维上进行2维tensor连接，得到新的多输入通道tensor（三维）

通过将核张量K与K+1（K中每个元素加1）和K+2连接起来，构造了一个具有3个输出通道的卷积核。

K = torch.stack((K, K + 1, K + 2), 0)
K.shape

result：
torch.Size([3, 2, 2, 2])

下面，我们对输入张量X与卷积核张量K执行互相关运算。现在的输出包含3个通道，第一个通道的结果与先前输入张量X和多输入单输出通道的结果一致。

corr2d_multi_in_out(X, K)

result：
tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
         [192., 224.]]])

• 1 X 1 卷积层

前言：1 x 1 卷积层失去了卷积的特性：有效提取相邻像素间的相关特征。而1 X 1 卷积 的唯一计算发生在channel上

下图所示，1X1 卷积核 与多输入多输出通道的互相关计算的输出中的每个元素，实质是输入图像中同一位置的元素的线性组合(2维)，最后连接维三维

如下图所示：

下面，我们使用全连接实现 1X 1 卷积。(因为 1X1 卷积操作 可以 化简为 全连接层 的操作)

def corr2d_multi_in_out_1x1(X,K):
    c_i,h,w=X.shape
    c_o=K.shape[0]
    X=X.reshape((c_i,h*w)) #整合为2维tensor
    K=K.reshape((c_o,c_i)) #整合为2维tensor
    #下面是用的是全连接层的矩阵乘法
    Y=torch.matmul(K,X) #全连接层的计算相当于 1X1的多输入输出通道的卷积层运算  1x1卷积核实质上不存在
    return Y.reshape((c_o,h,w)) 

当执行1×1卷积运算时，上述函数相当于先前实现的互相关函数corr2d_multi_in_out。让我们用一些样本数据来验证这一点。

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6

5.汇聚层

前言：

①处理图像时，我们希望逐渐降低隐藏表示的空间分辨率(即 w,h) 同时 汇聚信息。

②我们学习任务通常与全局图像问题有关(例：图像是否包含一只猫)，所以最后一层应该对最初的整个输入具有全局敏感性。通过逐步聚合信息，生成越发粗糙的映射，最终实现学习全局表示的目标，同时将卷积涂层的又是保留在中间层。

③当检测较底层特征时，我们希望**这些特征保持某种程度上的平移不变性。**若因为像素的短距离移动导致新图像的输出大不相同，则模型的稳定性过于差劲。所以我们采取汇聚层( pooling)

? 优点：1. 可以降低卷积层对位置的敏感性

? 2.可以降低对空间降采样表示的敏感性

• 最大汇聚层(maximum pooling)和平均汇聚层(average pooling)

与 卷积窗口类似，pooling同样存在汇聚窗口。汇聚窗口的移动与kernel 一样，但**操作区别是：**汇聚窗口计算每个窗口中tensor最大的元素值或者平均值，将该值作为新元素。

操作如下图所示：

汇聚窗口形状为p×q的汇聚层称为p×q汇聚层，汇聚操作称为p×q汇聚。

可以看出，即使输入数据在高度或宽度上移动一个元素，卷积层仍能识别到模式。

在下面的pool2d的函数中，我们实现pooling的前向传播。

注意：pooling不具有卷积核，汇聚窗口是虚拟，用于表达的媒介

import torch
from torch import nn
from d2l ipmort torch as d2l

def pool2d(X,pool_size,mode='max'):
    p_h,p_w=pool_size
    Y=torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
     Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

我们可以构建 上图中的输入张量X，验证二维最大汇聚层的输出。

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))

result：
tensor([[4., 5.],
        [7., 8.]])

此外，我们还可以验证平均汇聚层。

pool2d(X, (2, 2), 'avg')

result：
tensor([[2., 3.],
        [5., 6.]])

• 填充(padding)与 步幅 (stride)

前言：

与卷积层一样，pooling 也可以改变输出形状(是 h,w 不是通道) 。两者操作与卷积层操作一样，不再做阐述 (向下取整)

我们直接看下面例子：

们首先构造了一个输入张量X，它有四个维度，其中样本数和通道数都是1。

X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X

result：
tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])

默认情况下，深度学习框架中的步幅与汇聚窗口的大小相同。 因此，如果我们使用形状为(3, 3)的汇聚窗口，那么默认情况下，我们得到的步幅形状为(3, 3)。

是 nn.Maxpool2d() or nn.avePool2d() 的stride=kernel的size，而不是 nn.Conv2d()

pool2d = nn.MaxPool2d(3) # 3代表汇聚窗口大小为3，同样stride=3
pool2d(X)

result：
tensor([[[[10.]]]])

填充和步幅可以手动设定。

pool2d = nn.MaxPool2d(3, padding=1, stride=2) #汇聚窗口为3，填充为2，步长为2
pool2d(X)

result：
tensor([[[[ 5.,  7.],
          [13., 15.]]]])

当然，我们可以设定一个任意大小的矩形汇聚窗口，并分别设定填充和步幅的高度和宽度。

pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)

result：
tensor([[[[ 5.,  7.],
          [13., 15.]]]])

• 多个通道

在处理多通道输入数据时，汇聚层在每个输入通道上单独运算，而不是像卷积层一样在通道上对输入进行汇总。 这意味着汇聚层的输出通道数与输入通道数相同。 下面，我们将在通道维度上连结张量X和X + 1，以构建具有2个通道的输入。

X = torch.cat((X, X + 1), 1) #在第1维上进行连结，没有扩展维度
X
#shape为  （1，2，4，4）

tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]],

         [[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.],
          [13., 14., 15., 16.]]]])

如下所示，汇聚后输出通道的数量仍然是2。

pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)

tensor([[[[ 5.,  7.],
          [13., 15.]],

         [[ 6.,  8.],
          [14., 16.]]]])

6.卷积神经网络 (LeNet)

前言：

通过前面几节，我们学习了构造一个完整卷积神经网络所需要的组件。回想一下，在MLP中进行了分类问题，我们将大小为 28 X 28 的图片reshape 为 向量，从而用 全连接层进行了处理。

现在，我们学习了卷积神经网络：

它的好处是：①可以充分利用空间结构的特性

? ②卷积层模型更简洁、所需参数更少

本节我们介绍最早发布的卷积神经网络之一：LeNet

• LeNet

总体来看，LeNet 由两部分组成：

1. 卷积编码器：有两个卷积层组成
2. 全连接层密集块：由三个全连接层组成

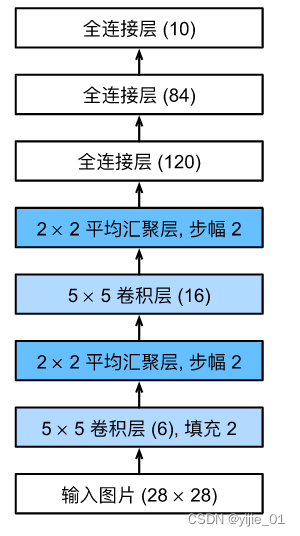
该架构如下图所示

每个卷积块基本单元是一个卷积层、一个sigmoid激活函数和 average pooling，注意，在LeNet诞生时 ReLU函数并未出现，所以这里的激活函数为 sigmoid。

注意：卷积的输出形状为四维(批量大小、通道数、高度、宽度)，为了将卷积块的输出传递给稠密块（即这里的三个全连接层），我们需要将这个四维输入reshape为 二维输入，即在小批量中展平每个样本。这里的二维输入中的第一个维度为小批量中的样本数，第二个维度为每个样本的平面向量表示。LeNet的稠密块 有三个全连接层，分别具有120、84、10个输出，因为我们在执行分类任务，所以输出层的10维对应于最后输出结果的数量。

如下图所示，我们会用代码实现该架构：

我们只需要实例化一个 Sequential 块将所需要的层来连接在一起

import torch
from torch import nn
from d2l import torch as d2l

#接下来我会详细展示后两维（h，w）的变化
#注意 kernel的四维为(in,out,h,w)  输入数据的四维为 (批量，in,h,w)
#为了讲解，我假设输入的X shape为 (1,1,28,28) 即一个批量，一个输入通道，高宽为28
net=nn.Sequential(
    # 28+2*2+1-5=28 即该卷积输出为 (1,6,28,28)
    nn.Conv2d(1,6,kernel_size=5,padding=2),nn.Sigmoid(),
    #  pooling层输出数据的输入通道=输入数据的输入通道， (28+2-2)/2=14 即 输出的 shape 为(1,6,14,14)
    nn.AvgPool2d(kernel_size=2,stride=2),
    # 14-5+1=10 即该卷积层输出数据的shape 为 (1,16,10,10)    
    nn,Conv2d(6,16,kerel_size=5),nn.Sigmoid(),
    # (10-2+2)/2=5 即 输出的shape 为  (1,16,5,5)
    nn.AvgPool2d(kernel_size=2,stride=2),
    #因为是输入从卷积块到稠密块，而全连接层只接受2维数据，所以nn.Flatten进行输入数据的展平.    第0维代表样本数，第1维代表一个样本的所有特征数
    nn.Flatten(),
    #展平后输入 shape为 (1,16*5*5),所以Linear的权重 shape为 (16*5*5,120) 
    #特征维度从16*5*5下降到120，样本数 即输出数据第0维大小不变 shape为(1,120)
    nn.Linear(16*5*5,120),nn.Sigmoid(),
    # 权重shape 为(120,84) 输出shape为 (1,84)
    nn.Linear(120,84),nn.Sigmoid(),
    # 权重shape 为(84,10) 输出shape为 (1,10),即一个样本对应十种分类
    nn.Linear(84,10))

下面，我们将一个大小为28×28的单通道（黑白）图像通过LeNet。通过在每一层打印输出的形状，我们可以检查模型，以确保其操作与我们期望的 下图一致。

X = torch.rand(size=(1, 1, 28, 28), dtype=torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape: \t',X.shape)

result：
Conv2d output shape:         torch.Size([1, 6, 28, 28])
Sigmoid output shape:        torch.Size([1, 6, 28, 28])
AvgPool2d output shape:      torch.Size([1, 6, 14, 14])
Conv2d output shape:         torch.Size([1, 16, 10, 10])
Sigmoid output shape:        torch.Size([1, 16, 10, 10])
AvgPool2d output shape:      torch.Size([1, 16, 5, 5])
Flatten output shape:        torch.Size([1, 400])
Linear output shape:         torch.Size([1, 120])
Sigmoid output shape:        torch.Size([1, 120])
Linear output shape:         torch.Size([1, 84])
Sigmoid output shape:        torch.Size([1, 84])
Linear output shape:         torch.Size([1, 10])

该结果证明了我们之前的分析！

• 模型训练

我们已经实现了LeNet，接下来我们看看Lenet在Fashion-MNIST数据集上的表现

batch_size=256
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size=batch_size)

为进行评估，我们实现如下函数（需要将数据集从内存复制到显存中） 用于测试集

def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
    """使用GPU计算模型在数据集上的精度"""
    if isinstance(net, nn.Module):
        net.eval()  # 设置为评估模式
        if not device:
            #如果未指定device 则将 模型所在的device 赋值给为None的device
            device = next(iter(net.parameters())).device
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list):
                #如果输入数据X 为list，就将X中的所有元素依次复制到 device
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X]
            else:
                #如果X不为list，则直接将X整体复制到device
                X = X.to(device)
            y = y.to(device)
            # 正确预测的数量，总预测的数量
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1] #返回该批量的准确精度

接下来，我们实现训练函数 train_ch6, 对于模型参数 我们将使用 Xavier 随机初始化方法。与全连接层一样，我们使用交叉熵损失函数和小批量随机梯度下降

def train_ch6(net,train_iter,test_iter,num_epochs,device):
    #使用GPU训练
    
    #定义模型参数的Xavier 初始化方法
    def init_weight(m):
        if type(m)==nn.Linear or type(m)==nn.Conv2d:
            nn.init.xavier_uniform_(m.weight)
    
    net.apply(init_weight)#进行模型参数初始化
    print('training on',device)
    #将模型整体（包括模型参数，计算的中间结果等）复制到device上进行计算
    net.to(device)
    #初始化优化器
    optimizer= torch.optim.SGD(net.parameters(),lr=lr)
    #指定损失函数，该损失函数进行了 softmax 操作，使得模型最终输出得到了规范化
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])
    
    timer, num_batches = d2l.Timer(), len(train_iter)#num_batches为批量样本数
    
    for epoch in range(num_epochs):
    # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train()#设为训练模式
        for i,(X,y) in enumerate(train_iter):
        #i为自然数索引，X为批量输入数据，y为批量的正确标签
        	timer.start()
            optimizer.zero.grad()#模型参数梯度清零
            X,y=X.to(device),y.to(device)
            y_hat=net(X)#得到预测标签
            l=loss(y_hat,y)
            l.backward()#损失函数关于模型参数进行求梯度(求偏导)
            optimizer.step()#权重更新，即卷积核权重
            with torch.no_grad():
                #训练损失之和，训练准确率之和，样本数
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop()
            train_l = metric[0] / metric[2]#每个epoch的损失精度
            train_acc = metric[1] / metric[2]#每个epoch的正确精度
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None))
        #得到每个epoch后模型的预测正确精度
        test_acc = evaluate_accuracy_gpu(net, test_iter)
        
        animator.add(epoch + 1, (None, None, test_acc))
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
          f'on {str(device)}')

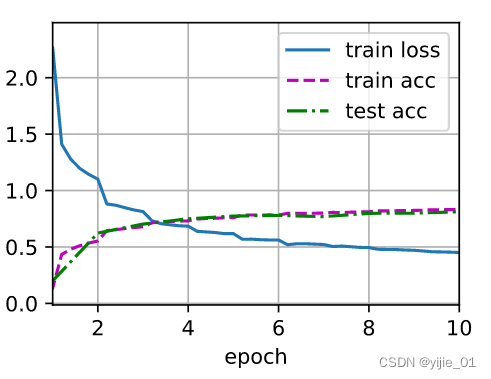
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

result：
loss 0.488, train acc 0.815, test acc 0.777
47229.5 examples/sec on cuda:0