情景(步长s为1):
一个6x6的图像,3x3的卷积核,每一行卷积的过程类似,如图
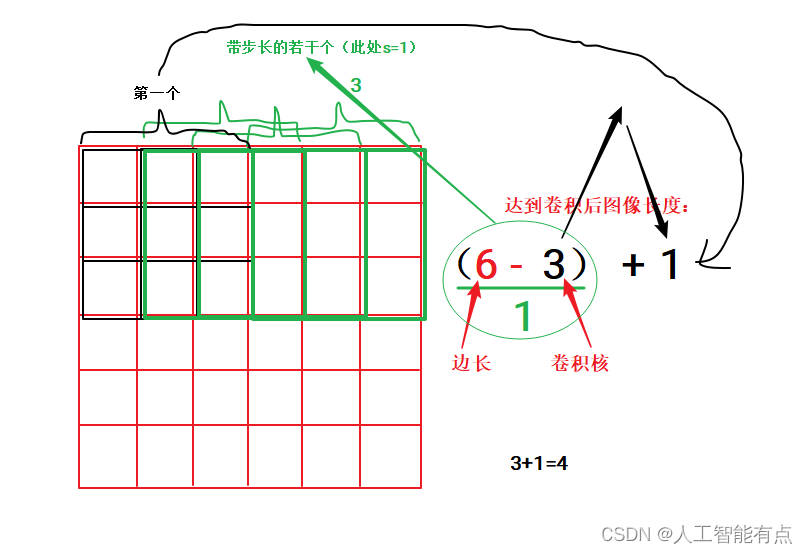
卷积核每走一步(第一个黑框到第一个绿框),输出一个像素。所以要计算卷积后图像的大小,需要知道图像大小及卷积核大小。
(6-3)+1的结果为4,所以得到的卷积图像大小为4x4。公式为(图片大小 - 卷积核大小) + 1,这里的(图片大小 - 卷积核大小)意味着卷积核移动的次数,移动3次(绿色框),输出3个像素,+1意味着第一次计算卷积,即卷积核初始位置不需要移动的那一次。
令原图像大小为nxn,卷积核大小为fxf。
所以在步长为1的情况下,则卷积后图像边长为((n-f)+1),即移动做卷积次数与第一次之和,图像大小为((n-f)+1) * ((n-f)+1)。
由此,可以暂时得到一个结论:nxn图像经过fxf卷积核得到图像大小的公式为((n-f)+1) * ((n-f)+1)
由上图能够明显看出,以上论述的情况的前提是卷积核每次移动一格,这里也是为了方便理解,上面情况是步长为1的情况,而有些时候,步长往往不为1,此时,卷积后的边长你是不是大概已经清楚了呢?
另外一种情景(步长不为1):
基于以上思考,假设当卷积核步长为3的时候,计算的过程依旧是将第一次卷积和移动次数相加得到边长,第一次卷积次数无疑就是1,只不过原来移动次数为n-f,而如今的卷积核移动得更快了,在n-f得总长度上加上由于步长变大的移动速度限制,一次移动3格。也就是说,现在的移动次数变为(n-f)/3,如图
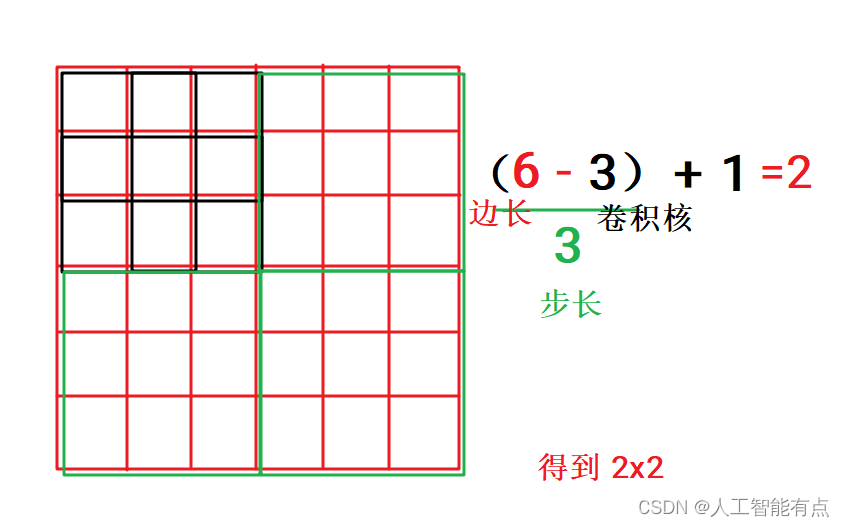
所以,可以得到公式,卷积后图像的长和宽为(n-f)/s + 1。
卷积存在问题
以上两种场景中,图像大小分别由6x6变为了4x4和2x2,原图像经过卷积操作得到的图像变小了。
缺点一:每次卷积,图像都会变小,6x6变为了4x4,6x6变为了2x2,多做几次卷积,你的输出图像会变得很小,可能变成1x1的大小,图像变小,会失去很多有用信息,因此图像变小是一个缺点。
缺点二:情景一中,图像边缘角落的像素点(边上四个角)仅被卷积计算了一次,因为它在3x3卷积核的一角,卷积核移动后,不能够再次对其计算。而区域中心被多次计算,边缘区域像素点在输出中采用较少,意味着丢失掉了边缘位置的信息。
填充
为了解决这些问题,可以在原始图像周围添加一些像素点,如果把6x6图像填充成8x8图像,那么经过3x3卷积,(8-3)+1=6,得到的就是6x6的图像。习惯上,用0填充。如果p是填充数量,在情景一中,p=1,因为我们在周围一圈填充了像素点,输出变成了((n+2p - f) + 1)*((n+2p - f) + 1),(6+2-3+1)(6+2-3+1)=6x6与输入大小相同。
通过填充,角落像素信息发挥的作用较小这一缺点就被削弱了。这里我们填充的像素p=1。实际上填充多少像素,通常有两种选择,Valid卷积和Same卷积。
Valid卷积
Valid卷积意味着不填充。当你有nxn的图像,fxf的卷积核,s=1,将会输出一个(n-f+1)(n-f+1)的图像,这类似情景一。6x6图像,通过3x3卷积核,得到一个4x4输出。
Same卷积(一般用在s=1情况)
Same卷积,见名知意,填充之后,你的输出大小和输入大小是一样的。
s=1情况
s=1,根据n-f+1,填充后n变成n+2p,输出边长为n+2p-f+1。因此如果有nxn图像用p个像素填充,输出的大小就是(n+2p - f + 1)(n+2p - f + 1)。如果你想让n+2p - f + 1=n,使输入输出大小相等,你会通过等式求解p,那么p=(f-1)/2。
另外一种理解方式可以是把卷积核中心放在图像边缘上,这样的起始条件,填充相当于去掉卷积核中心一排的一半(p=(f-1)/2),使得输出和输入相同。
s !=1 情况
根据(n-f)/s + 1,填充后n变成n+2p,输出边长为(n+2p - f)/s + 1。因此如果有nxn图像用p个像素填充,输出的大小就是((n+2p - f)/s + 1)((n+2p - f)/s + 1)。如果你想让(n+2p - f)/s + 1=n,使输入输出大小相等,你会通过等式求解p,那么p=(s(n-1)+f-n)/2。
注:一般情况下Same卷积不会有s>1情况,因为就算s=2,实际的图像比较大,移动损失的像素点很多,要填充的话,就填充很多像素,然而当填充像素很多,意义就不大了。所以Same模式一般是s=1。
所以当f是一个奇数的时候,只要选择相应的填充尺寸,你就能确保得到和输入相同尺寸的输出。这也是为什么前面的例子,当过滤器是3×3时,使得输出尺寸等于输入尺寸,所需要的填充是(3-1)/2,也就是1个像素。另一个例子,当你的过滤器是5×5,如果f=5,然后代入那个式子,你就会发现需要2层填充使得输出和输入一样大,这是过滤器5×5的情况。
习惯上,计算机视觉中,f通常是奇数,甚至可能都是这样。你很少看到一个偶数的过滤器在计算机视觉里使用,我认为有两个原因。
其中一个可能是,如果f是一个偶数,那么你只能使用一些不对称填充。只有f是奇数的情况下,Same卷积才会有自然的填充,我们可以以同样的数量填充四周,而不是左边填充多一点,右边填充少一点,这样不对称的填充。
第二个原因是当你有一个奇数维过滤器,比如3×3或者5×5的,它就有一个中心点。有时在计算机视觉里,如果有一个中心像素点会更方便,便于指出过滤器的位置。
也许这些都不是为什么f通常是奇数的充分原因,但如果你看了卷积的文献,你经常会看到3×3的过滤器,你也可能会看到一些5×5,7×7的过滤器。后面我们也会谈到1×1的过滤器,以及什么时候它是有意义的。
但是习惯上,推荐你只使用奇数的过滤器。我想如果你使用偶数f也可能会得到不错的表现,如果遵循计算机视觉的惯例,我通常使用奇数值的f。
你已经看到如何使用padding卷积,为了指定卷积操作中的padding,你可以指定p的值。也可以使用Valid卷积,也就是p=0。也可使用Same卷积填充像素,使你的输出和输入大小相同。以上就是padding,在接下来的笔记中我们讨论如何在卷积中设置步长。
参考:https://www.jianshu.com/p/4d3ec56e7d05