作者 Johannes Ballé? ? Google Scientist
论文下载? ??https://arxiv.org/abs/1611.01704
论文主页(包括源码、数据集、可视化结果等)? ? http://www.cns.nyu.edu/~lcv/iclr2017/
论文代码(训练、测试代码,其他预训练模型)? ? https://github.com/tensorflow/compres
论文评论(其他人和作者的评论等)?End-to-end Optimized Image Compression | OpenReview
作者本人在PCS2108上做的口头汇报? ?https://www.youtube.com/watch?v=x_q7cZviXkY
本文主要参考以下两篇博客整理而成,加入了其他自己的理解
2017-ICLR-END-TO-END OPTIMIZED IMAGE COMPRESSION | お前はどこまで見えている
端到端的图像压缩------《End-to-end optimized image compression》笔记_叶笙箫的博客-CSDN博客_端到端的压缩
目录
0 总述
论文提出一个基于CNN的端到端图像压缩框架,它由使用非线性分析变换(编码器)、均匀量化器(多进制四舍五入)和非线性综合变换(解码器)组成。最终RD性能和MS-SSIM都比JPEG和JPEG-2000好。这个框架是后来被大家广泛使用的超先验(Hyperprior)框架的基础。
论文提出的框架如下图,这是一种通用的非线性变换编码架构。编码过程:原图x,通过参数为Φ的分析变换y=ga(x;Φ),映射到编码空间(code space)中量化得离散值的向量q。码率R是量化后的q直接估计的,R不小于q的熵。
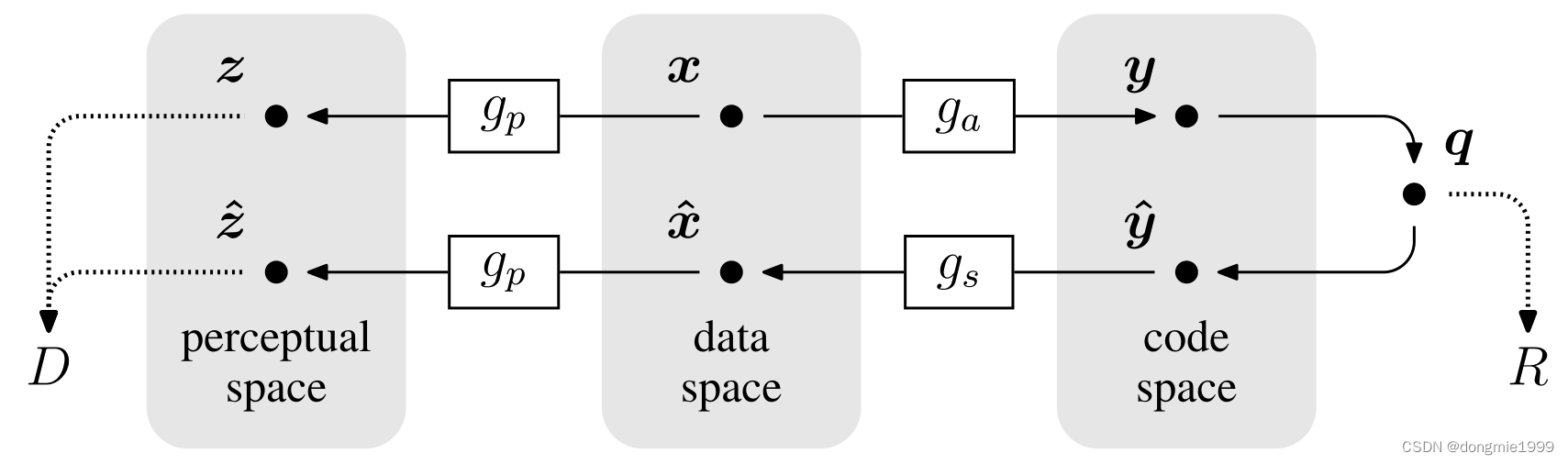
这个框架在Balle2016年ICLR的论文End-to-end optimization of nonlinear transform codes for perceptual quality就提出来了。本文中,作者对此进行了进一步介绍,给出了该框架下的一个实际模型,并给出了充足的理论分析和实验来验证该模型的有效性。在此模型中,分析变换(编码器)共3层,每层用了卷积层+下采样+GDN的结构优化MSE,如下图左;而综合变换(解码器)采用分析变换的近似逆结构,也是3层不过反着来,每层IGND+上采样+卷积,如下图右。量化使用的是均匀的标量量化。
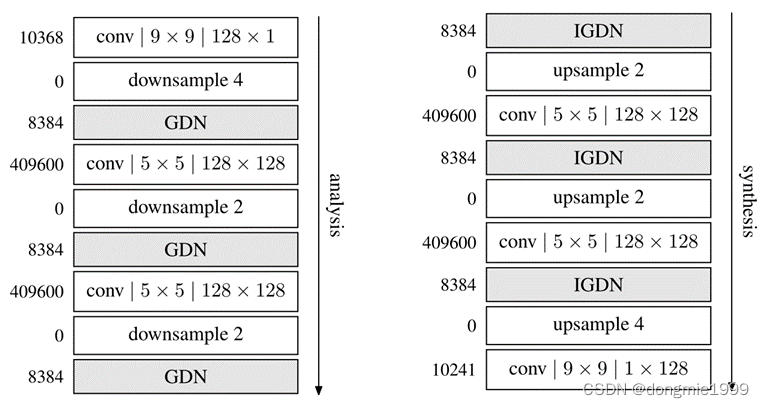 ?
?
?对于RD曲线上的每个点,都直接使用梯度下降优化方法同时联合优化分析综合变换。对于均匀标量量化模块梯度几乎处处为 000 的问题,作者给出了一种连续的近似均匀标量量化来替代原来的离散均匀量化。最后,作者对量化后的数据使用了一个熵编码得到实际的比特流,从而计算该模型实际的码率,以此来验证该模型的有效性。[1]
1?关于GDN
其中使用的GDN是作者2015年DENSITY MODELING OF IMAGES USING A GENERALIZED NORMALIZATION TRANSFORMATION提出来的(论文原文看了一眼,翻译成中文我也看不懂)。GDN可以看做是更适合图像重建的BN层。GDN在这篇文章被使用后,因为效果不错,做end-to-end图像压缩的也都跟着用。
之前大多数压缩方法都是建立在正交线性变换基础上,目的是为了降低数据间的相关性,从而简化后续的熵编码。但是线性变换输出之间的联合统计特性展现了很强的高阶依赖。这个问题可以通过使用局部增益控制操作(最早来源于生物神经元领域)来很好地解决,于是作者使用了他自己之前提出的 GDN 模型来替代线性变换(在那篇文章中作者已经验证了GDN具有很好的高斯化图像数据的能力)。[1]
???????1.1?为什么要归一化
神经网络学习过程的本质就是为了学习数据分布,如果我们没有做归一化处理,那么每一批次训练数据的分布不一样,从大的方向上看,神经网络则需要在这多个分布中找到平衡点,从小的方向上看,由于每层网络输入数据分布在不断变化,这也会导致每层网络在找平衡点,显然,神经网络就很难收敛了。当然,如果我们只是对输入的数据进行归一化处理(比如将输入的图像除以255,将其归到0到1之间),只能保证输入层数据分布是一样的,并不能保证每层网络输入数据分布是一样的,所以也需要在神经网络的中间层加入归一化处理。[2]
归一化后有什么好处呢?原因在于神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
对于深度网络的训练是一个复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。[3]
1.2 常用归一化方法举例——BN
1.2.1 BN层定义
与激活函数层、卷积层、全连接层、池化层一样, BN (Batch Normalization) 层也属于CNN中网络的一层。BN本质原理上是将数据归一化至:均值0、方差为1;BN层是可学习的,参数为γ、β的网络层[4]。BN已经成为许多先进深度学习模型的重要组成部分,特别是在计算机视觉领域。它通过批处理中计算的平均值和方差来规范化层输入,因此得名[5]。
BN是针对一个batch里的数据进行归一化和尺度操作,且一旦神经网络训练完成后,BN的尺度参数也固定了,这就是一个完全变成一个关于归一化数据的仿射变换,其数学公式描述如下:
???????1.2.2?BN层优点
BN层归一化数据接近于高斯分布,解决了训练时候中间层数据分布发生改变的问题。而且BN层允许选择更大的学习率,可以加速训练[6]。此外,BN解决了深度梯度消失和梯度爆炸的问题;BN还可以改善正则化策略:作为正则化的一种形式,轻微减少了对dropout的需求,不用管过拟合中drop out、L2正则项参数的选择问题[7]。
???????1.2.3?BN层缺点
BN层每次处理的批量的均值和标准差都不同,所以这相当于加入了噪声,增强了模型的泛化能力。但对于图像超分辨率重建、图像生成、图像去噪和图像压缩等生成模型,就不友好了,生成的图像要求尽可能清晰,不应该引入噪声[8]。

当batch size越小,BN的表现效果也越不好(好像最好batch>32),因为计算过程中所得均值和方差不能代表全局[9]。
注:后针对这个问题,何恺明团队提出了GN(group normalization),先把通道C分成G组,然后单独拿出来归一化,最后把G组归一化之后的数据合并成CHW,解决了batch很小时BN效果不好的问题[10]。
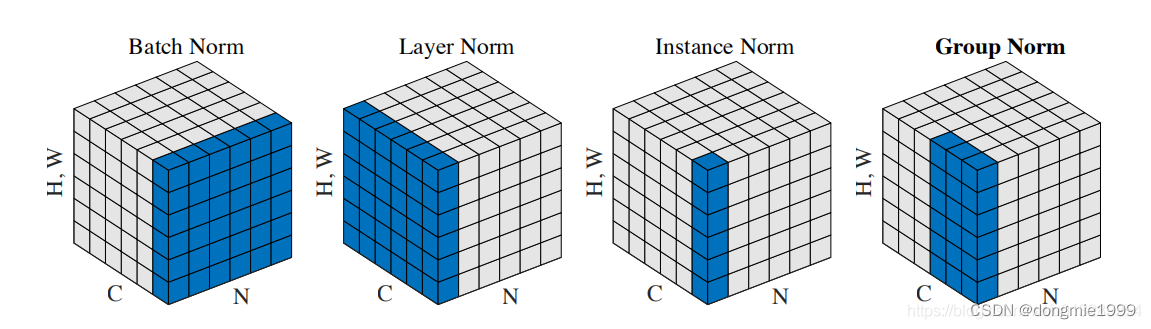 ?
?
???????1.3?GDN的定义和优点
注意,GDN本质也是一种归一化方法,但和经常在神经网络里看到的BN不是同一类型的归一化。BN是针对一个batch里的数据进行归一化和尺度操作,且网络训练完成后BN的尺度参数也固定了,这就是一个完全关于归一化数据的仿射变换,BN数学公式描述如下:
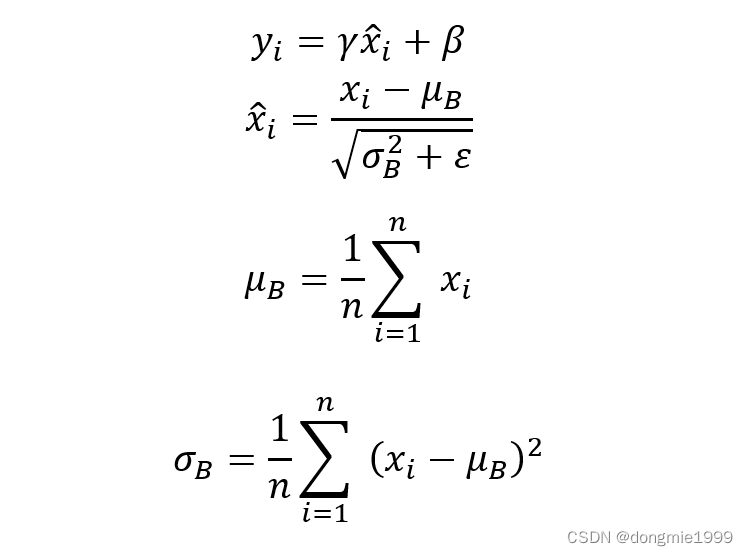
?而GDN的归一化和尺度操作对整幅图像都是一致的,相当于一种空间自适应的归一化操作,而且GDN是非线性的,其公式描述如下
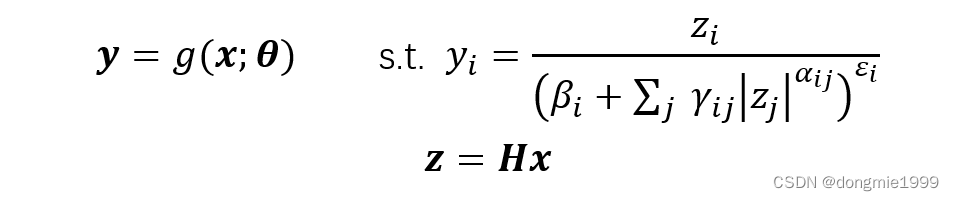
2 模型优化
再看一眼框架图,整个编码器是卷积+下采样+GDN组成的,已经知道GDN是干啥的了,再看看变换和量化(卷积的参数)是如何选择的。
?
2.1 优化目标函数
为了得到参数的最优解,我们想要对损失函数L=λD+R求关于各个模块的参数的偏导,然后梯度下降求近似最优解

?2.2?变换模块
?这篇长达27页的文章并没有详细展开说变换怎么做的,因为作者本人一直在做非线性变换,这里使用的变换在他2016年发表的文章《End-to-end optimization of nonlinear transform codes for perceptual quality》中有详细介绍。(其实下面量化模块使用的方法也是这篇文章中就提出来的,这篇文章还挺硬核充满数学公式。。。有空该看看的(真的好难看啊))
所采用的变换模块其实就是GDN作为编码器的分析变换 ![]() ,对输入x进行参数为
,对输入x进行参数为![]() 的变换后得y,GDN变换
的变换后得y,GDN变换![]() 的数学描述为
的数学描述为

平方确保在参数值接近0时梯度更小,否则优化可能变得不稳定。为获得一个明确的映射,我们在每个梯度步骤后将每个 ![]() ?投影到区间
?投影到区间 ![]() ?上。我们对
?上。我们对 ![]() ?和进行了相同的处理,并另在每一步之后用转置取
?和进行了相同的处理,并另在每一步之后用转置取![]() ?的平均值,以使其对称。GND的反变换IGDN参数处理方式相同。
?的平均值,以使其对称。GND的反变换IGDN参数处理方式相同。
为了消除每个线性变换及其后续非线性(或在综合变换中为之前的非线性)之间的尺度模糊,我们在每个梯度步骤之后对线性滤波器进行了重新规范化,将每个滤波器除以其平方和系数的平方根。对于分析变换,求和遍历空间和所有输入通道,对于综合变换,求和遍历空间和所有输出通道。其中线性滤波器利用离散余弦变换(DCT)系数进行参数化。DCT比DFT在加速收敛方面更有效。
2.3 量化模块
求导的过程中,由于量化是不可导的(如下图),这篇文章为了使用随机梯度下降优化,训练加了一个噪声然后做区间内积分来近似代替多进制四舍五入量化,而测试的时候直接四舍五入量化量化。这种近似代替解决了量化不可微的问题,使得网络可以训练,但测试是直接量化和加入均匀噪声模拟量化的方法出来差得最多好像有0.2dB。
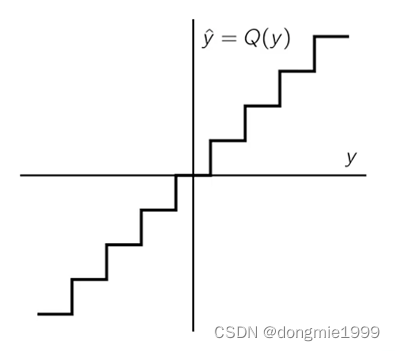
?去掉量化模块后,本应直接对图像变换后进行熵编码;但是变换后量化前系数通常也不可导,因为它的分布像是个拉普拉斯分布(中间有个奇点),如下图。为解决这个问题,加入[-0.5, 0.5]之间的随机归一化噪声,加了之后得到的看起来像下图虚线(连续且近似可微)
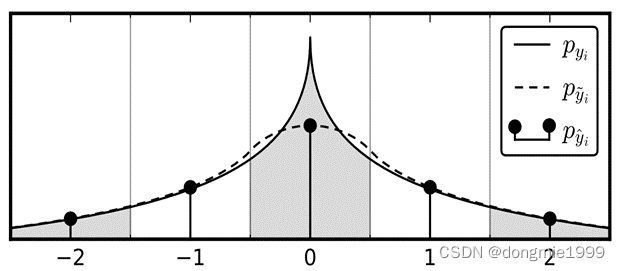
?![]() ?:变换后待量化元素
?:变换后待量化元素
![]() ?:四舍五入后的变换系数
?:四舍五入后的变换系数
![]() ?:通过添加噪声后的变换系数
?:通过添加噪声后的变换系数
上述是三者的概率密度函数(PDF),离散的 ![]() ?是概率质量函数(PMF),其中黑点的数值由实线在各自区间内取积分得到的,但是其实不一定等于虚线在区间内的积分,只能是近似关系。即可以通过这种近似关系,合理等于两者的微分熵,就是说加均匀噪声后,不影响码率估计。这样积分后相当于每个区间得到一个值,跟量化/采样是一样的,从连续区间映射到一个离散值。
?是概率质量函数(PMF),其中黑点的数值由实线在各自区间内取积分得到的,但是其实不一定等于虚线在区间内的积分,只能是近似关系。即可以通过这种近似关系,合理等于两者的微分熵,就是说加均匀噪声后,不影响码率估计。这样积分后相当于每个区间得到一个值,跟量化/采样是一样的,从连续区间映射到一个离散值。
实验结果说明,这种加噪声后积分的量化方法既不影响码率,也不影响MSE。左图为量化带来的MSE和加均匀噪声带来MSE的关系,右图为离散情况下的bpp以及可微分情况下的bpp的关系。可得,本文提出的量化模型及熵率估计模型与实际中量化引起的误差和待编码值得熵率近似一致。
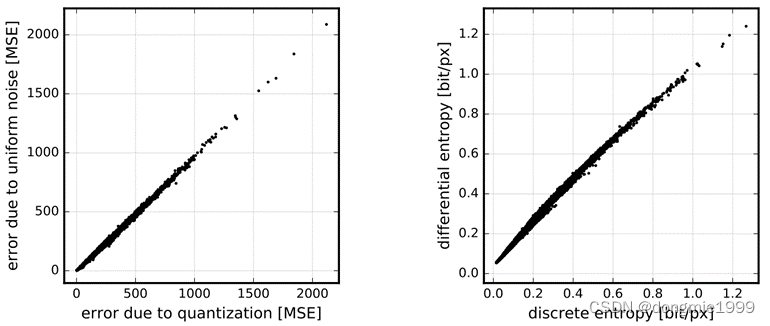
?加了噪声之后有两个好处:
首先,y=y+Δy?的密度函数是q的概率质量函数的连续松弛;
其次,独立的均匀噪声就其边际矩而言近似于量化误差,并且经常被用作量化误差的模型(Gray and Neuhoff,1998)
针对y的宽松概率模型和熵代码在code space中假设独立的边际,则通过进行参数建模以减少码率估计模型与实际模型之间的差距,具体使用精细采样的分段线性函数,这些函数与一维直方图的更新类似(请参见附录)。即通过神经网络生成编码点的概率质量函数PMF,通过PMF的积分求得每个特征点对应的可导形式的概率值,通过对概率值求自信息得到估计的码率点,在前向传播中,通过训练阶段生成的神经网络生成分位点与累积分布函数CDF,将CDF与待编码点输出range coder进行熵编码。
由于编码数值的概率密度函数被均匀噪声平滑,这部分会导致一定的误差,但是通过减小采样间隔可以使得模型误差任意小。
把离散的标量换成连续的近似标量量化后,最终目标损失函数式可写成如下形式:

?其中向量 ψ(i)?是![]() ?的分段线性逼近的参数。这是连续可微的,适合随机梯度下降优化。
?的分段线性逼近的参数。这是连续可微的,适合随机梯度下降优化。
其中各个参数与模块的对应关系如下图
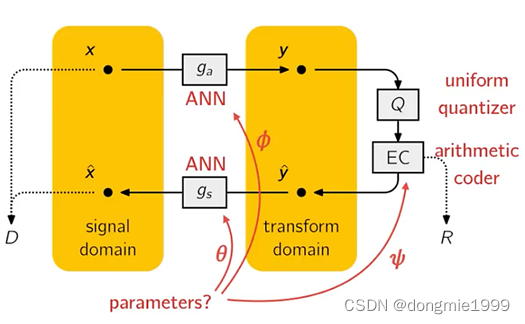
?上式的损失用MSE度量,即整体框架图中的 ![]() ?是一个固定的变换,直接计算恒等式
?是一个固定的变换,直接计算恒等式
?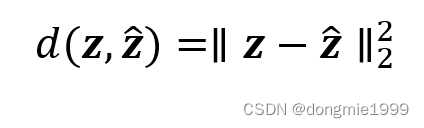
?在之前的《End-to-end optimization of nonlinear transform codes for perceptual quality》中,在感知域中用的变换 ![]() ?是作者本人二作的另一篇文章《Perceptual image quality assessment using a normalized Laplacian pyramid》中提出来的NLP (Normalized Laplacian Pyramid),而不是设置成恒等式直接算MSE。在感知域中使用NLP做变换可能性能更好(也会增加时间复杂度)。
?是作者本人二作的另一篇文章《Perceptual image quality assessment using a normalized Laplacian pyramid》中提出来的NLP (Normalized Laplacian Pyramid),而不是设置成恒等式直接算MSE。在感知域中使用NLP做变换可能性能更好(也会增加时间复杂度)。
?2.4?熵编码模块
虽然作者提出了一种离散量化的近似连续量化操作,但即用连续的量化操作,仍然不知道量化后数据所服从的分布 ![]() ?,我们只能得到量化后的数据
?,我们只能得到量化后的数据![]() ?,也无法直接计算出目标损失函数中的码率项,也就无法优化损失函数。为此,作者又提出了一种近拟计算码率的方法,即为每个量化区间中加噪声后积分得到的离散值
?,也无法直接计算出目标损失函数中的码率项,也就无法优化损失函数。为此,作者又提出了一种近拟计算码率的方法,即为每个量化区间中加噪声后积分得到的离散值 ![]() ?设定一个可学习的参数向量 ψ(i)?,其中的元素看成是从分布
?设定一个可学习的参数向量 ψ(i)?,其中的元素看成是从分布 ![]() ?中采样得到的,采样密度为每单位长度采样 10 个点。然后通过使用 SGD (就是普通随机梯度下降法,stochastic gradient descent)最大化下面的负的期望似然函数来优化参数 ψ(i)?:
?中采样得到的,采样密度为每单位长度采样 10 个点。然后通过使用 SGD (就是普通随机梯度下降法,stochastic gradient descent)最大化下面的负的期望似然函数来优化参数 ψ(i)?:
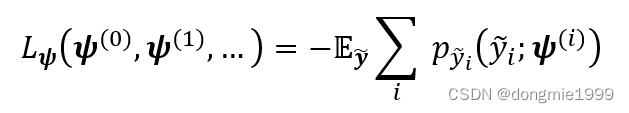
?对于变换和反变换的参数?和θ使用Adam算法来算最优值,使用的Adam算法的初始值![]() ,当R和D都不显著改变时候,把
,当R和D都不显著改变时候,把![]() 缩小10倍,一直到
缩小10倍,一直到![]() 。Adam和其他SGD变种见【https://zhuanlan.zhihu.com/p/152566066】
。Adam和其他SGD变种见【https://zhuanlan.zhihu.com/p/152566066】
在计算 ![]() ?时,将
?时,将![]() ?表达成分段线性函数,过参数向量 ψ(i)?中的那些点。然后将
?表达成分段线性函数,过参数向量 ψ(i)?中的那些点。然后将 ![]() ?代入即可计算得到
?代入即可计算得到![]() ?。整个近似过程都是可微的,故能够使用梯度下降来优化 ψ(i)?和码率。
?。整个近似过程都是可微的,故能够使用梯度下降来优化 ψ(i)?和码率。
实际熵编码过程中,作者提出了一种类似CABAC的熵模型。该熵模型主要编码信息:
- 图像的大小:两个 16比特的整数(不使用 CABAC 算法);
- 图像类型:灰度图或 RGB 图,1比特表示(不使用 CABAC 算法);
- 模型参数:使用一个16比特的整数,来表示分析综合变换的模型参数 λ 的索引(一般训练好模型参数后,会发给编解码端)
量化后图像数据q:将q在空间上光栅扫描并在通道上依次迭代处理形成一串数据流,再使用 CABAC 算法进行压缩
对量化后的q,用一个决策树来进行二进制化,对于每个 ![]() ,我们首先测试编码的值是否等于分布的模式。如果是这样,则
,我们首先测试编码的值是否等于分布的模式。如果是这样,则 ![]() ?的编码完成;如果不是,另一个二进制判定决定它是比众数大还是小。
?的编码完成;如果不是,另一个二进制判定决定它是比众数大还是小。
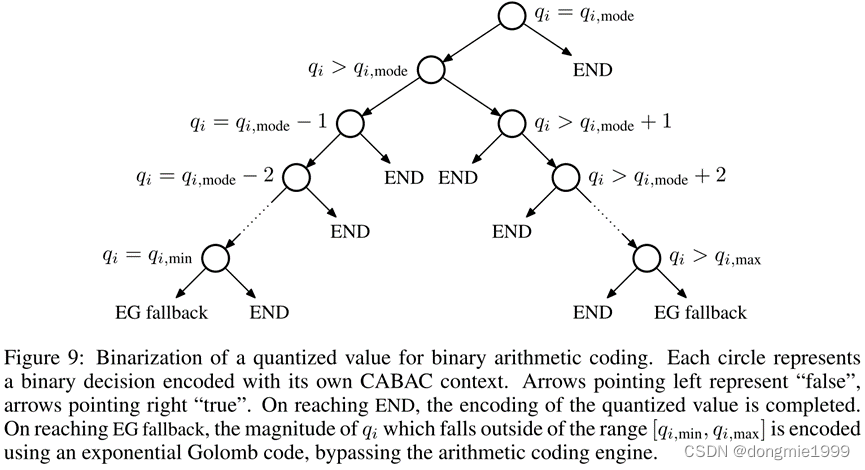
?每次往左决策,即 +0?;往右决策,即 +1?。最终得到落在区间 ![]() ?的所有
?的所有 ![]() ?值的二进制编码,再使用 CABAC 进行压缩。对于不在
?值的二进制编码,再使用 CABAC 进行压缩。对于不在 ![]() ?的
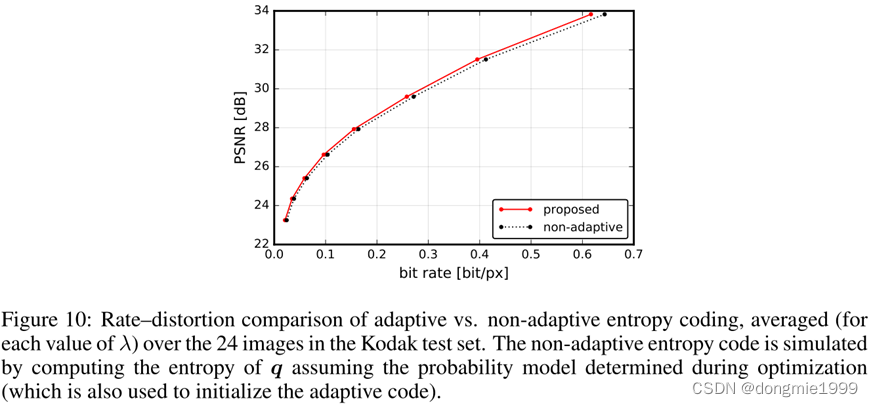
?的 ![]() ?值,使用指数哥伦布码进行压缩(也是借鉴于 H.264)。作者在 Kodak 数据集上进行实验,验证了这种基于上下文的自适应压缩算法是优于传统的确定性压缩算法的。
?值,使用指数哥伦布码进行压缩(也是借鉴于 H.264)。作者在 Kodak 数据集上进行实验,验证了这种基于上下文的自适应压缩算法是优于传统的确定性压缩算法的。
?
3 实验结果
使用随机梯度下降法在由6507张图像组成的ImageNet的一个子集上联合优化了全套参数φ, θ和所有ψ(做训练)。每一个λ训练一次。实验结果表明,在Kodak数据集上,本文提出的端到端图像压缩方案比JPEG和JPEG2000的RD性能要好。
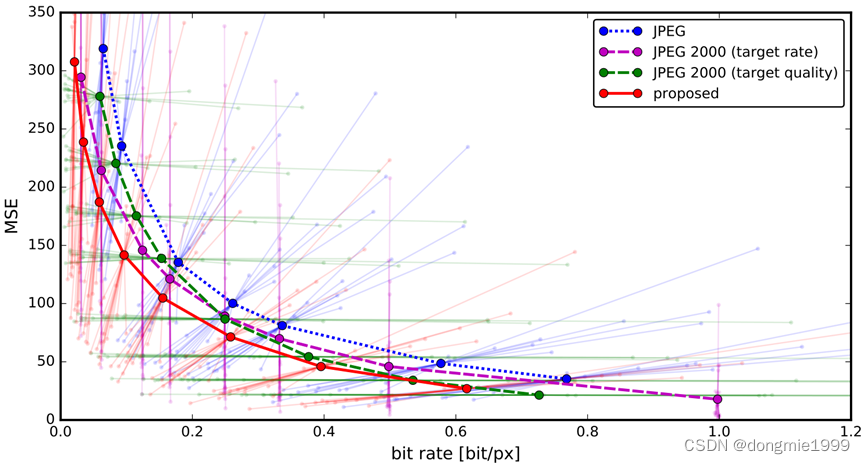
?一些可视化结果对比
