梯度
神经网络中最为核心的概念,梯度。
梯度是一个向量,
第一,梯度的长度大小表达了某种趋势,第二,梯度的方向代表着增长(大值)的方向,朝着函数越来越大的方向走。
找到极小值
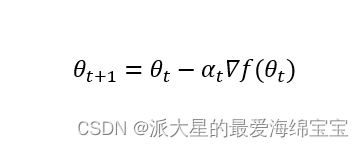

αt一般设置的比较小,可以更好地找到极小值。
除了马鞍的鞍点影响优化器,也就是搜索的过程外,还有:
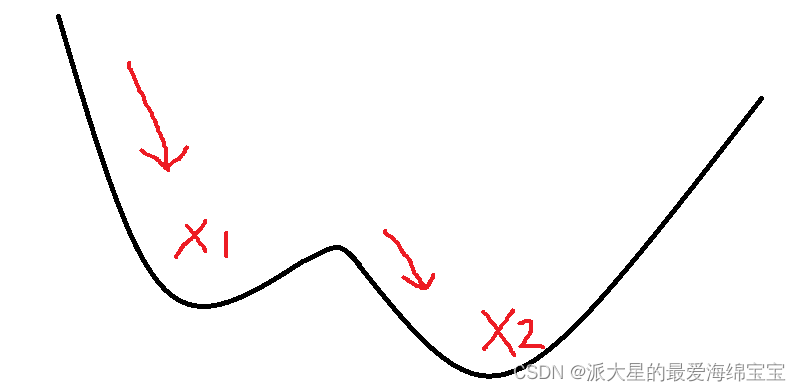
1.初始状态

如果你的初始值在A点,很有可能当你到达x1时,得到局部最小值后就停止了。
2.学习率
当我们的学习率比较大时,步长就会比较大,可能下一个点直接就跨过了最小值到另一边了,对于一些较好的函数,可能会通过左右震荡,最终会收敛到最小值点。但大部分情况都是,最后无法收敛。最开始最好把学习率设置的小一点,例如0.01,0.001,若是收敛了,则慢慢增加学习率,训练的速度会变快,如果不收敛,则继续减少学习率。学习率还会影响训练的精度,有的时候,会不断在最小值左右震动,就是无法到达最小值点,此时需要慢慢减小学习率。
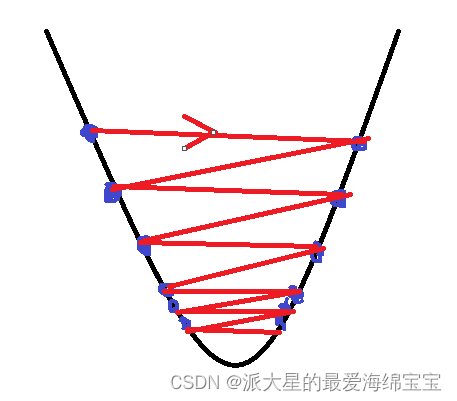
3.动量(怎么逃离局部最小值)
我们会添加一个动量,这个动量可以理解为一个惯性,帮助走出这个局部最小值。
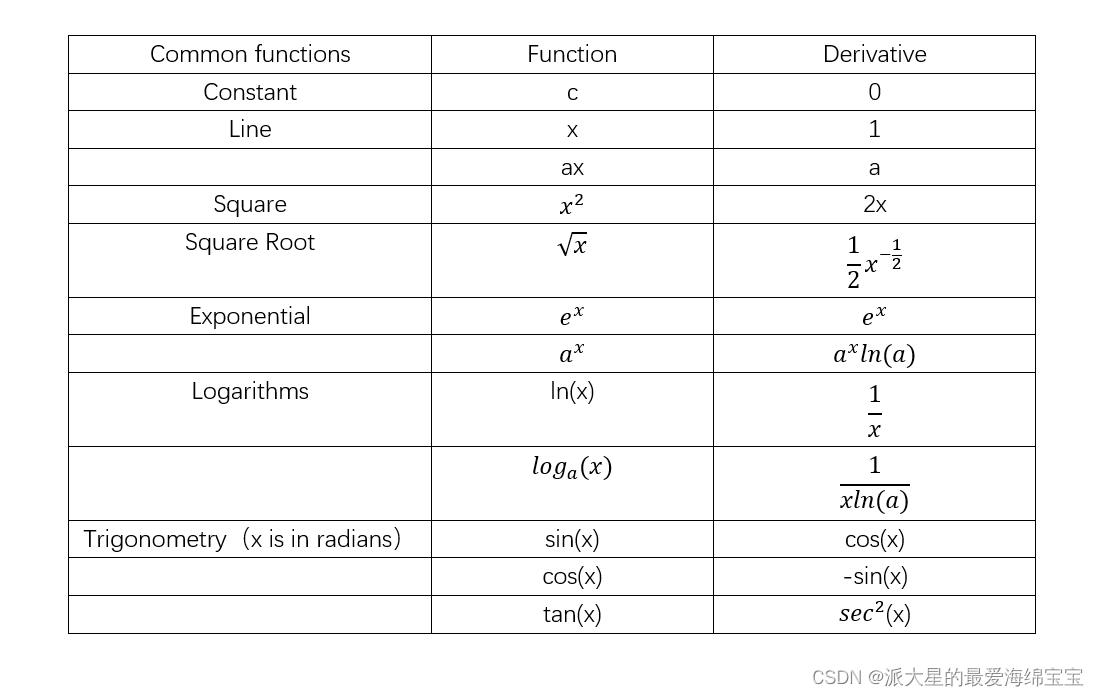
常见的函数梯度
梯度API
求梯度
1.torch.autograd.gard(loss[w1,w2,…])
loss对w求导
2.loss.backward()
直接进行w1.grad
激活函数及其梯度
激活就是指在x必须大于某个数后,才会激活,输出一个电平值。
激活函数存在一个重要概念,就是不可导。不能使用梯度下降的方法进行优化。使用启发式搜索来求解最优解。
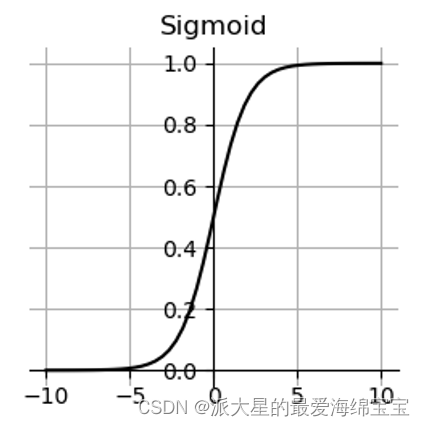
1.torch.sigmoid()
比较适合模拟生物学上神经元的机制。Sigmod是可导的,
Sigmod导数=Sigmod(1-Sigmod)
Sigmod函数是连续的光滑的,且函数值压缩在0到1之间,概率、RGB都可以使用Sigmod函数。
缺点:梯度离散现象,求最优解时,因为x趋近于无穷小时等于0,loss保持不变,使得我们的最优解一直无法更新。

import torch
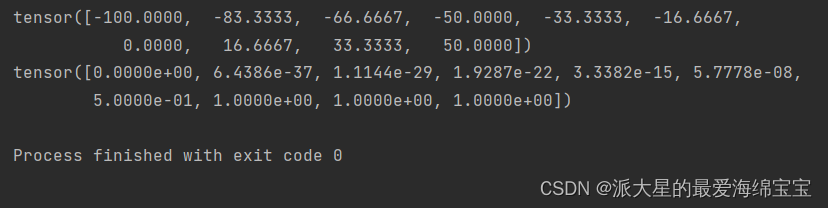
a=torch.linspace(-100,50,10)
print(a)
print(torch.sigmoid(a))
2.torch.tanh()
在RNN中常用。
tanh的导数=1-tanh**2
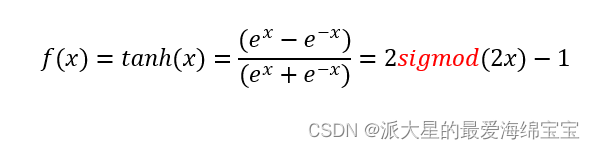
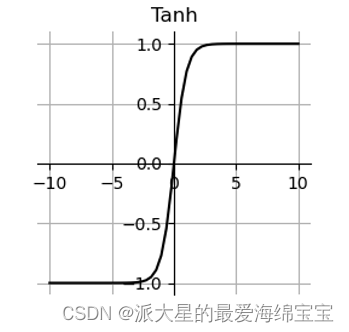
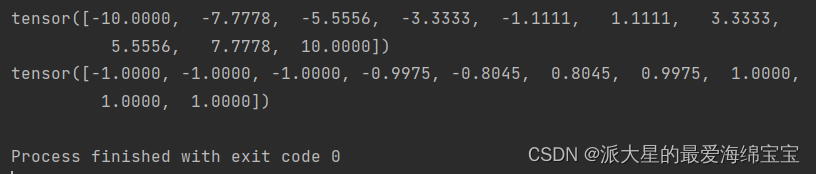
a=torch.linspace(-10,10,10)
print(a)
print(torch.tanh(a))
3.torch.relu()
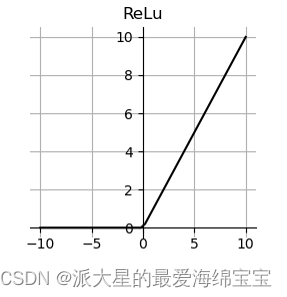
ReLU(Rectified Linear Unit)是深度学习奠基石的激活函数,使用最多的。
做research时优先选择relu。
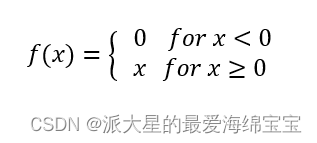
当x小于0时不激活,且梯度是0,当x大于0时,线性激活,且梯度是1。导数计算起来非常简单,且不会放大缩小。
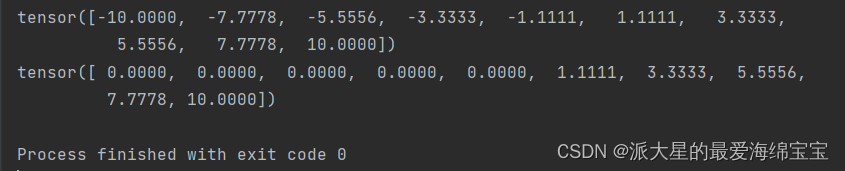
a=torch.linspace(-10,10,10)
print(a)
print(torch.relu(a))
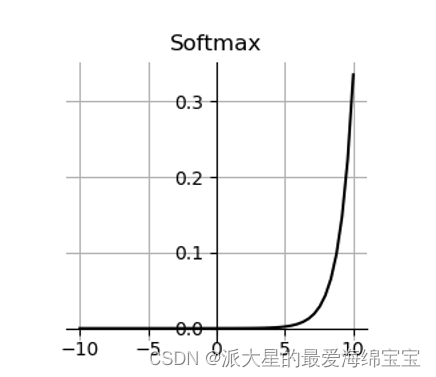
4.softmax
与Cross Entropy Loss结合的激活函数。
首先,每个区间的概率值在0到1之间,且概率之和等于1,适合多分类问题。
pi对aj求导,当i=j时,得pi(1-pj),当i≠j时,得-pipj。

刚开始2是1的2倍,俩个值的概率大于2倍,即会把大的放的更大,把小的放的更密集,使差距变得更大。
a=torch.rand(3)
p=torch.softmax(a,dim=0)
print(p)
必须写dim。
Loss
1.MSE(优先使用)
Mean Square Erro

采用torch.norm求解MSE,则torch.norm(y-pred,2)*pow(2),第一个2代表L2。
2.Cross Entropy Loss交叉熵
1.Cross Entropy Loss
熵entropy在信息学上的定义:
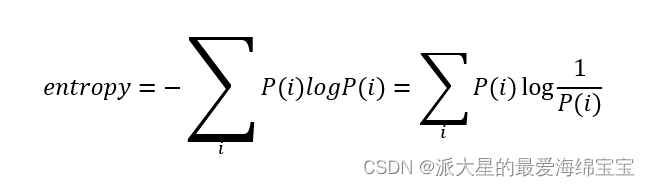
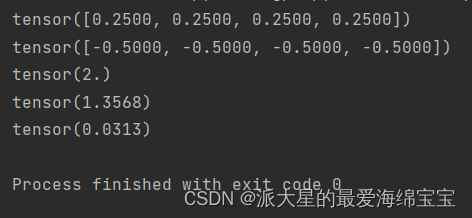
a=torch.full([4],1/4.)
print(a)
print(a*torch.log2(a))
print(-(a*torch.log2(a)).sum())
b=torch.tensor([0.1,0.1,0.1,0.7])
print(-(b*torch.log2(b)).sum())
c=torch.tensor([0.001,0.001,0.001,0.999])
print(-(c*torch.log2(c)).sum())
对于a,这四个数的增长度一样,熵较大,比较稳定。
对于b,前三个数的增长度较小,最后一个数增长都比较高,熵大概是1.3568,不稳定的。
对于c,前三个数代表发生概率极低,最后一个是极高,最后熵是0.0313,如果是这四分数中的幸运儿,则更加惊喜,因为这种情况发生概率很低。
从上到下越来越好,使我们朝着目标前进。

Dkl求散度,判断两者的重叠情况。
p=q
当p和q相等时,交叉熵就会等于某一个分布的熵
for one-hot encoding
若分布是[0,1,0,0],只有这一项的概率是1,则1log1=0,则H(p)=0。
实例
import torch
import torch.nn.functional as F
x=torch.randn(1,784)
w=torch.randn(10,784)
logits=x@w.t()
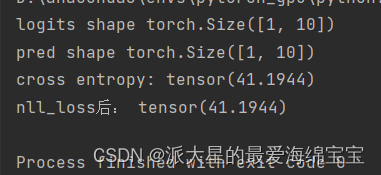
print('logits shape',logits.shape)
pred=F.softmax(logits,dim=1)
print('pred shape',pred.shape)
pred_log=torch.log(pred)
print('cross entropy:',F.cross_entropy(logits,torch.tensor([3])))
print('nll_loss后:',F.nll_loss(pred_log,torch.tensor([3])))
logits=xw+b
logits经过softmax函数后,得到pred
pred经过log函数,得到pred_log
使用cross entropy,此时必须使用logits,cross entropy把softmax和log在一起了。
cross entropy=softman+log+nll_loss,cross entropy相当于这三个操作一起。
2.binary classification
f:x->p(y=1|x)
如果p(y=1|x)>0.5(已经确定的阈值),预测为1,其他情况预测为0
求entropy
目标函数是-[ylog(p+(1-y)log(1-p))]

3.muti-class classification
f:x->p(y=y|x)
多类:p(y=0|x),p(y=1|x),…,p(y=9|x),每个的概率都是0到1,且总概率值为1。可通过softmax实现。
3.Hinge Loss
4.分类问题为什么不选择MSE
在一些前沿问题上,假如cross entropy不行时,可以选择使用MSE进行尝试
- sigmoid+MSE会很容易出现梯度离散现象
- cross entropy更大,梯度信息更大,收敛的更快。