[人工智能]神经网络和自动控制的联系

以下从两个方面讲述，正向使用即不带误差传播，在神经网络上直接是正向传播过程。误差传播过程在神经网络中被称为误差反向传播

正向使用上的差别

神经网络和自动控制的关系，类似于对偶，假设我们有一个线性系统：

y=ax+b

神经网络的侧重在于：

输入一个x得到对应的y

而自动控制的侧重在于：

输入一个y得到对应的x

误差反馈上的差别

神经网络的侧重在与得到对应的系统:

得到系统参数a，使得输入x能得到y

而自动控制的侧重在于得到对应的输入

得到输入x，使得在a参数下系统能输出y

控制的误差曲线：PID算法

我们先列公式，后面再讲解：

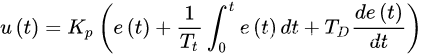
假如初始0时刻系统输入u为x，目标输出为y1，当前系统实际输出是y，还差很多才能到达y1，我们如何调整u使得输出能为y1？

或者换个说法，我们输入为y1，如何得到对应的输出u？

我们使用误差曲线来描述，输入为x时，输出的误差是多少，当误差降为0时我们就找到了对应的u。

对于线性系统，我们似乎可以很容易找到 u(x) - e(x)函数的解析式： u(x) = k * e(x) + b
我们只要令e(x)=0，就能得到目标输出为y1时，系统输入u(x)=b，但是为了保证系统变化的连续性，我们不会立马令u=b，而是缓慢的来:
$u(t_0)=x，u(t_1)=x+k，u(t_1)=x+2k,...u(t_n)=b，u(t_{n+1})=b$

这个b怎么求呢，初始0时刻u(t0)=x，t时刻u(tn)=b，我们可以用积分来求

$b=u(t_0)+\Delta u$
$\Delta u=u(t_n)?u(t_0))={\int }_{t_0}^{t_n}{u}^{{}^{\prime }}(t)dt=(t_n?t_0)?k$

在原始公式中，我们可以把$\frac{ke(t)}{T_t}$看着此处的$u^{{}^{\prime }}(t)$

对于线性系统，有上述两项也就够了，而非线性系统，也可以将其局部进行线性化，然后使用，但对于非线性系统，参数k也就不是一个定量而是变量

增量变化

之前我们说了，让u慢慢增加，即：
$u(t)=u(t_0)+(t?t_0)?u^{{}^{\prime }}(t)$

或者采用递推式：$u(t)=u(t?1)+u^{{}^{\prime }}(t)$

实际上，更为有效的做法是，误差比较大时我们用步长大点，误差小时步长小一点：
$u(t)=u(t?1)+k?e(t)$

我们试问还能更好的变化吗？

我们对$e(t)$在t处进行二阶泰勒展开：
$e(t+m)=e(t)+m?e^{{}^{\prime }}(t)+\frac{m^2}{2}?e^{{}^{\prime \prime }}(t)$
后面两项是对未来e(t)变化率的预测，我们还可以加上这两项，令du为：
$du(t+m)=k?[e(t)+m?e^{{}^{\prime }}(t)+\frac{m^2}{2}?e^{{}^{\prime \prime }}(t)]$

则有：
$u(t)=u(t?1)+du(t+m)$

$du(t+m)=k?[e(t)+m?e^{{}^{\prime }}(t)+\frac{m^2}{2}?e^{{}^{\prime \prime }}(t)]$

m决定了预测的远近，预测太远了系统会出现震荡，有的地方只使用一阶展开而不使用二阶展开。

神经网络的误差曲线

这个通常用误差反向传播来完成，也是先求目标和当前输出得到误差，然后用误差去得到w的变化量，举例来说线性网络：

y=wx+b

当前输入为x，目标输出为y1，实际输出为y，得到误差e(t)= y1 - y。根据确定的x，得到 w(t)- e(t)误差曲线，我们假设为线性系统：

w(x) = k * e(x) + b

在神经网络中，一般也不使用二阶预测，直接用

$w(t)=w(t?1)+k?e(t)$