开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> OpenCV：05滤波器 -> 正文阅读

[人工智能]OpenCV：05滤波器

滤波器的 "波"指噪声，而滤波即把噪声过滤掉，或者是把一些特征或有特点的东西过滤出来

卷积

什么是图像卷积

图像卷积就是卷积核在图像上按行滑动遍历像素时不断地相乘求和的过程
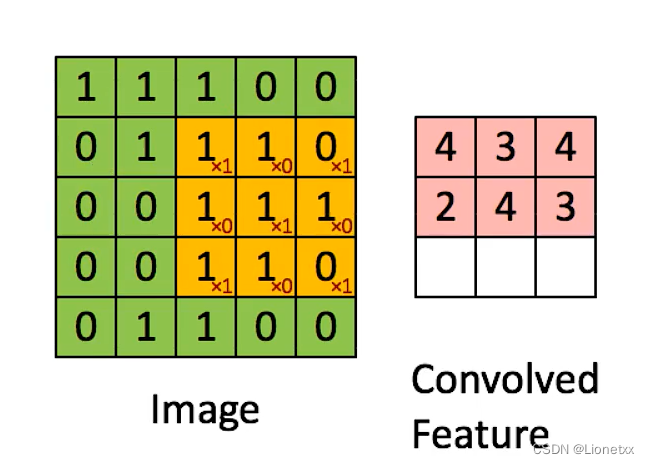
在这里插入图片描述

步长`Stride`

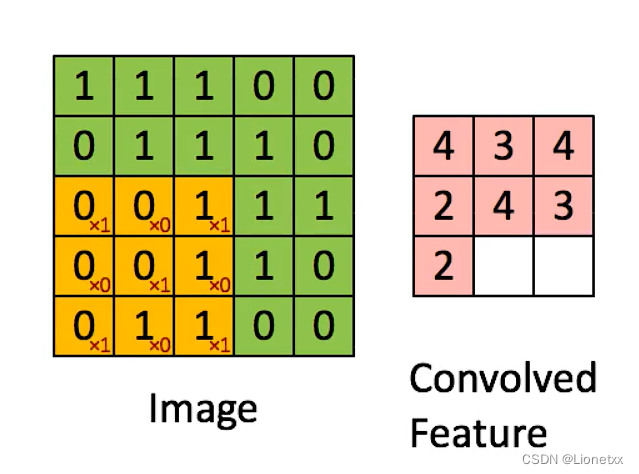
步长就是卷积核在图片上移动的步幅。上面例子中卷积核每次移动一个像素步长的结果，如果将这个步长改为2，结果会如何？

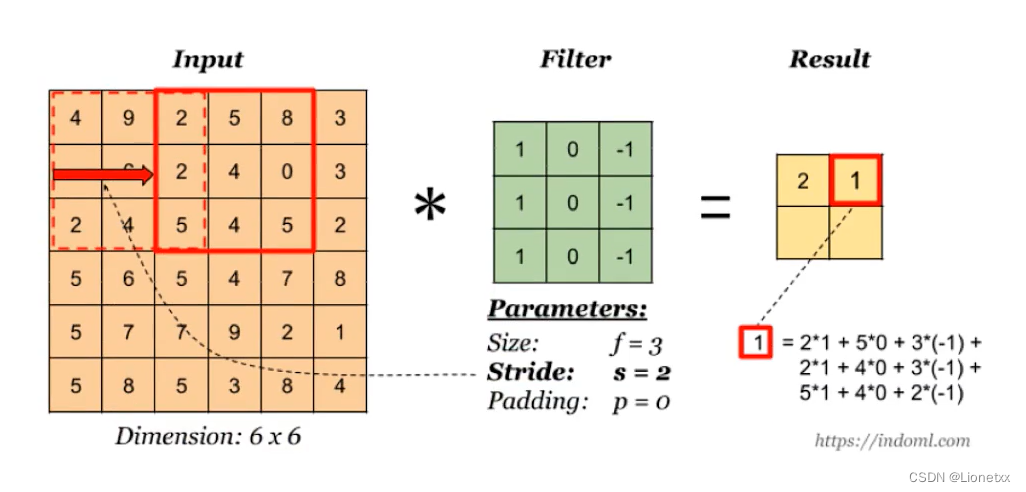
在这里插入图片描述

`Padding`补丁

从上面的例子我们可以看出：卷积操作完成后图片的长宽变小了，如果要保持图片的大小不变，我们需要在图片周围填充0 ——> padding补丁指的就是补充0的圈数

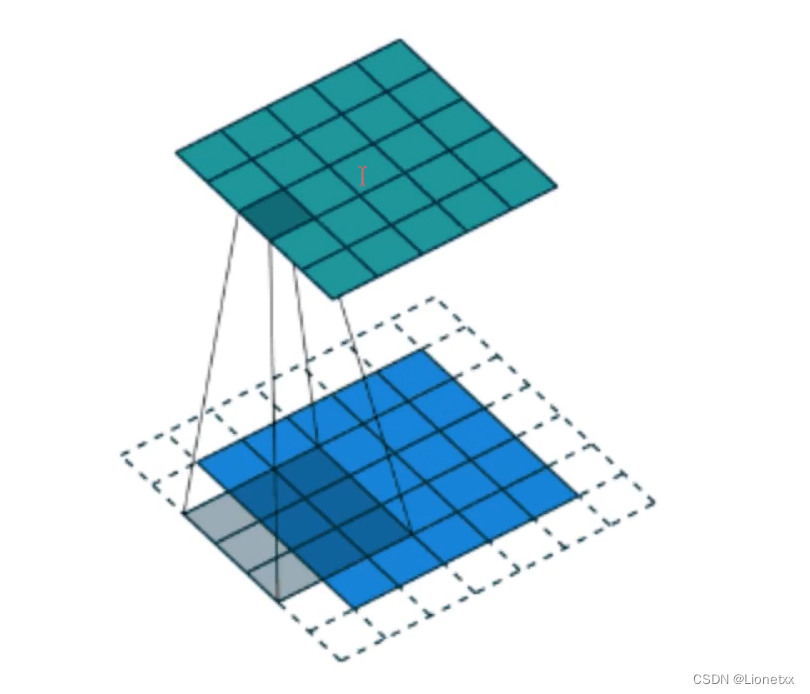
在这里插入图片描述

我们可以通过公式计算出需要补0的圈数
H：高度、W：宽度、D：通道数

输入图片体积大小：H1 * W1 * D1
四个超参数：
- 卷积核Filter的数量K
- 卷积核Filter的大小F(大小一般都是奇数：如3×3、5×5)
- 步长s
- 零填充大小P(padding)
输出图片体积大小：H2 * W2 * D2
- H2 = (H1 - F + 2P) / S + 1
- W2 = (W1 - F + 2P) / S + 1
- D2 = K

如我们有个28 × 28的图片，用 5 × 5的卷积核计算，结果图片的大小为 (此时未加补丁且步长为1) ：

H2 = (28 - 5 + 2*0 )/ 1 + 1 = 24；
W2 = (28 - 5 + 2*0 )/ 1 + 1 = 24

如果我们想加补丁，使得卷积运算前后图片大小一致，则让等式前后相等

H2 = (28 - 5 + 2*P )/ 1 + 1 = H1 = 28；
W2 = (28 - 5 + 2*P )/ 1 + 1 = W1 = 28

解出P = (F - 1 ) / 2，得P = 2

卷积核的大小

图片卷积运算中，卷积核一般为奇数，比如3×3、5×5、7×7，为什么一般是奇数呢，出于以下两个方面得考虑：

根据上方padding的计算公式，如果要保持图片大小不变，采用偶数卷积核的话，比如4*4，将会出填充1.5圈零的情况
奇数维度的卷积核(或称为“过滤器”)有中心，便于指出过滤器的位置，即opencv中卷积的锚点

卷积案例

关键API：cv2.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])
其中：

ddepth：卷积之后图片的位深，即卷积之后图片的数据类型，一般设为默认值-1，表示和原图类型一致
kernel：卷积核大小，用元组或ndarray表示，要求数据类型必须是float
dst：目标，可选参数，一般不用写(用于C++中)，我们只需要用一个变量接受函数返回值即可
anchor：锚点，即卷积核的中心点，是可选参数，默认是(-1,-1)
delta：可选参数，表示卷积运算后额外加上的一个值，相当于线性方程中的偏差，默认是0
borderType：边界类型，一般不设

# opencv中的卷积操作
import cv2
import numpy as np

# img = cv2.imread('./11.jpeg')
# img = cv2.imread('./cat.jpeg')
img = cv2.imread('./dog.jpeg')

# 设置一个全为1的卷积核(类型必须是float32) ——> 全为1相当于什么也没做，任何像素乘上1还是它本身
kernel_0 = np.ones((5,5) , np.float32)/25 # /25相当于对该5×5的卷积核做平均

# 尝试其他卷积核 ——> 突出轮廓
kernel_1 = np.array([ [-1,-1,-1],[-1,8,-1],[-1,-1,-1] ]) # 中间的8为强化强素，而-1为弱化，相当于模糊周边像素，强化突出中心

# 尝试其他卷积核 ——> 浮雕效果
kernel_2 = np.array([ [-2,1,0],[-1,1,1],[0,1,2] ]) # 中间的8为强化强素，而-1为弱化，相当于模糊周边像素，强化突出中心

# 尝试其他卷积核 ——> 锐化效果
kernel_3 = np.array([ [0,-1,0],[-1,5,-1],[0,-1,0] ]) # 中间的8为强化强素，而-1为弱化，相当于模糊周边像素，强化突出中心

# 卷积操作
# dst = cv2.filter2D(img,-1,kernel_0)   # 相当于啥也没做
# dst = cv2.filter2D(img,-1,kernel_1) # 突出轮廓
# dst = cv2.filter2D(img,-1,kernel_2) # 浮雕效果
dst = cv2.filter2D(img,-1,kernel_3) # 锐化效果

cv2.imshow('img',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
在这里插入图片描述
图片变得模糊了，因为我们这里的卷积效果相当于每一个像素点都变成了周围25个像素点(卷积核大小为5*5)的平均值

突出轮廓
在这里插入图片描述

浮雕效果
在这里插入图片描述

锐化
在这里插入图片描述

滤波

方盒滤波与均值滤波

方盒滤波

关键API：cv2.boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]]])
其中：
方盒滤波的卷积核是固定的，[ ]里全是1，外面乘上a
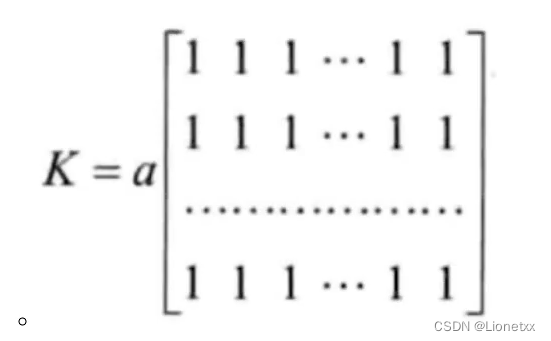
在这里插入图片描述

参数normalize：中文意思为标准化，
- 当normalize = True时，a = 1 / (W * H)滤波器的宽高，相当于加起来是1，我们刚刚写的kernel_0的效果是一样的，使得图片变模糊
- 当normalize = False时，a = 1
- 一般情况下我们都使用normalize = True的情况，这时方盒滤波等价于均值滤波
其余的参数和上面一样
不用手动创建卷积核，只需要告诉方盒滤波，卷积核的大小（长宽）是多少

# opencv中的方盒滤波
import cv2
import numpy as np

img = cv2.imread('./dog.jpeg')

# 不用手动创建卷积核，只需要告诉方盒滤波，卷积核的大小（长宽）是多少
dst = cv2.boxFilter(img,-1,(5,5),normalize = True)

cv2.imshow('img',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
在这里插入图片描述

均值滤波

关键API：cv2.blur(src, ksize[, dst[, anchor[, borderType]]])
其中：

blur的中文意思为模糊不清的事物，使看不清，因此均值滤波做的事情就是把图片模糊化
均值滤波没有位深ddepth参数

# opencv中的均值滤波
import cv2
import numpy as np

img = cv2.imread('./dog.jpeg')

# 不用手动创建卷积核，只需要告诉均值滤波，卷积核的大小（长宽）是多少
dst = cv2.blur(img,(5,5))

cv2.imshow('img',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
在这里插入图片描述

高斯滤波

注意：卷积核 = 高斯模板 = 滤波器

高斯滤波的关键就是找到一个符合高斯分布的卷积核

其实和前面几种滤波没有区别，都是靠窗口(卷积核)去扫描图片，只是高斯滤波的窗口中的数字符合高斯分布（也叫正态分布）

要理解高斯滤波首先要知道什么是高斯函数：高斯函数是在符合高斯分布（或叫正态分布）的数据中的概率密度函数（x轴是数据，y轴是该数据可能出现的概率），画出来长这样子

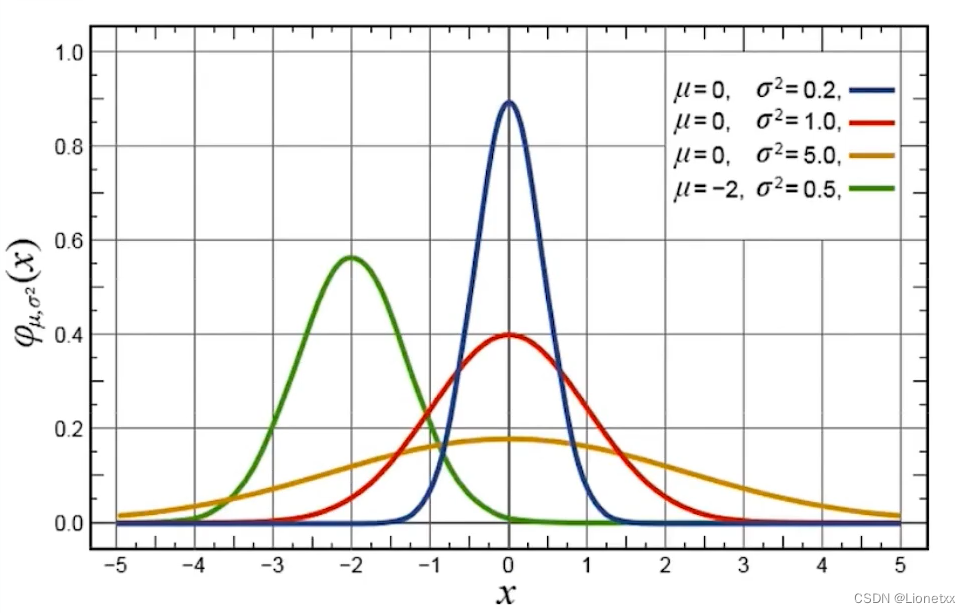
在这里插入图片描述
高斯函数的特点是以x轴某一点（这一点称为均值）为对称轴，越靠近中心数据发生的概率越高，最终形成一个两边平缓、中间陡峭的钟型（帽型）图形；

在图中可以看出：方差σ^2越大的数据越分散，图像越矮越胖；方差 σ^2越大的数据越集中，图像越高越尖；

高斯函数的一般形式：

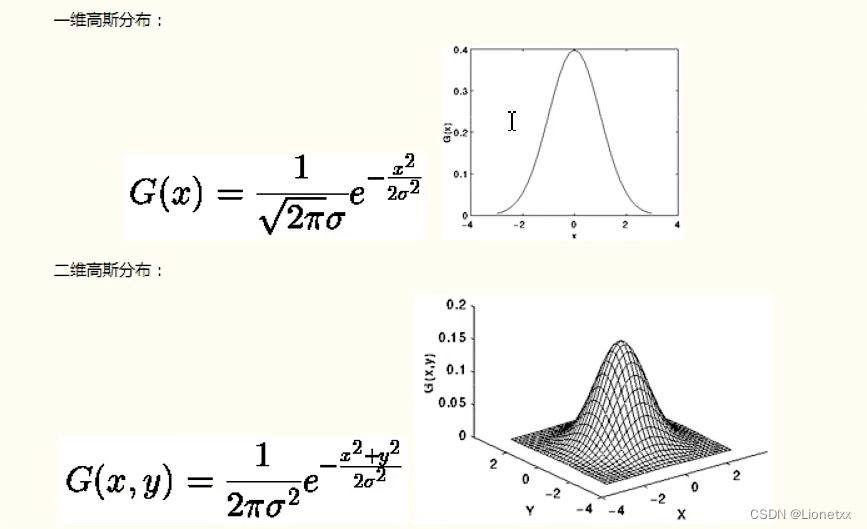
在这里插入图片描述
高斯滤波就是使用符合高斯分布的卷积核对图片进行卷积操作，所以高斯滤波的重点就是如何计算高斯分布的卷积核，即高斯模板

假定中心点的坐标为(0,0)，那么取距离它最近的8个点的坐标，为了计算，需要设置σ的值，假定σ = 1.5，则

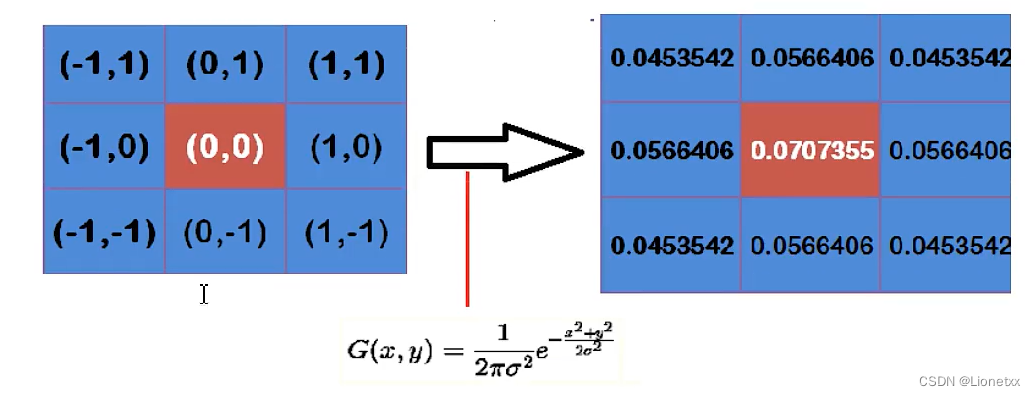
在这里插入图片描述
我们可以观察到越靠近中心，数值越大；越靠近边缘，数值越小，符合高斯分布的特点！

通过高斯函数计算出来的是概率密度函数，所以我们还要确保这九个点加起来为1，这九个点加起来的权重总和为0.4787147，因此上面的9个值还要分别除以总数0.4787147（相当于这个值出现的概率），得到最终的高斯模板

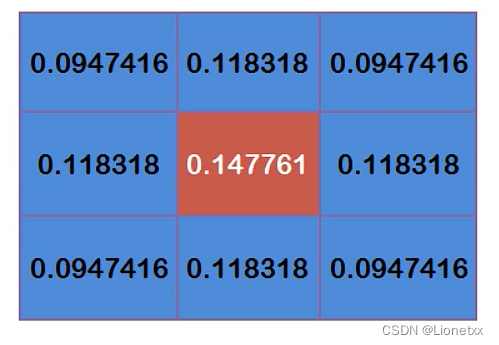
在这里插入图片描述
注意：有些高斯模板是在归一化（标准化）后的高斯模板基础上再用每个数除以左上角的值，然后向下取整

有了卷积核后，计算高斯滤波就简单了。假设现在有9个像素点，则灰度值（0-255）的高斯滤波计算如下：
在这里插入图片描述

最左边的图为原图的灰度值
中间的图片为卷积操作：对应位置相乘
最右边的图为结果

将右图的九个点加起来，就得到了中心点高斯滤波的值，对所有点重复这个过程，就得到了高斯模糊后的图像

关键API：cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])
其中：

src：原图
ksize：高斯模板（卷积核）大小 ——> 写元组！
sigmaX：X轴的标准差
sigmaY：Y轴的标准差，默认为0，此时sigmaX = sigmaY
如果没有指定sigmaX的值，则会默认从ksize的高度和宽度去计算sigma

选择不同的sigma会得到不同的平滑效果，sigma越大，平滑效果越明显
在这里插入图片描述

没有指定sigma时，ksize越大，平滑效果越明显
在这里插入图片描述

# opencv中的高斯滤波
import cv2
import numpy as np

img = cv2.imread('./fakeface.jpeg')

# 不用手动创建卷积核，只需要告诉高斯滤波，卷积核的大小（长宽）是多少
# 高斯滤波
dst = cv2.GaussianBlur(img,(5,5),sigmaX = 1000)

cv2.imshow('img',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
图像变模糊了
在这里插入图片描述

中值滤波

中值滤波的原理非常简单，假设有一个数组[1,5,5,6,7,8,9]，取其中的中间值（即中位数）作为卷积后的结果值即可。中值滤波对胡椒噪音（也叫椒盐噪音）效果明显

关键API：cv2.medianBlur(src, ksize[, dst])
注意：

此处的参数ksize要求是整形，而不是元组！

# opencv中的均值滤波
import cv2
import numpy as np

img = cv2.imread('./girl.png')

# 不用手动创建卷积核，只需要告诉中值滤波，卷积核的大小（长宽）是多少
# 中值滤波
dst = cv2.medianBlur(img,5)

# 我们对比一下高斯滤波：效果不好！
# dst = cv2.GaussianBlur(img,(5,5),sigmaX = 1)

cv2.imshow('img',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
椒盐噪声被滤掉了很多！
在这里插入图片描述
高斯滤波处理：
效果不好！

原因：中值滤波在遍历时，直接使用图片最中心的那个点，这个点很有可能是没有噪声的，因此这整一块都没有噪声

双边滤波

双边滤波既可以实现局部的降噪处理，又可以保留边缘信息

双边滤波可以实现美颜（磨皮）的效果

双边滤波对于图像的边缘信息能够更好地保存。其原理为一个与空间距离相关的高斯函数与一个与灰度距离相关的高斯函数相乘

在这里插入图片描述

双边滤波的本质是高斯滤波，双边滤波和高斯滤波的不同点在于：双倍滤波既利用了位置信息又利用了像素信息来定义滤波窗口的权重。而高斯滤波只定义了位置信息

在图片中的颜色交界处，前一个像素点是一个颜色，后一个像素点又变成了另一个颜色，图片的灰度值会出现断崖式的变化，这就是我们的双边滤波需要考虑进去的东西，我们称之为灰度距离（高斯滤波只考虑空间距离），如划线部分：

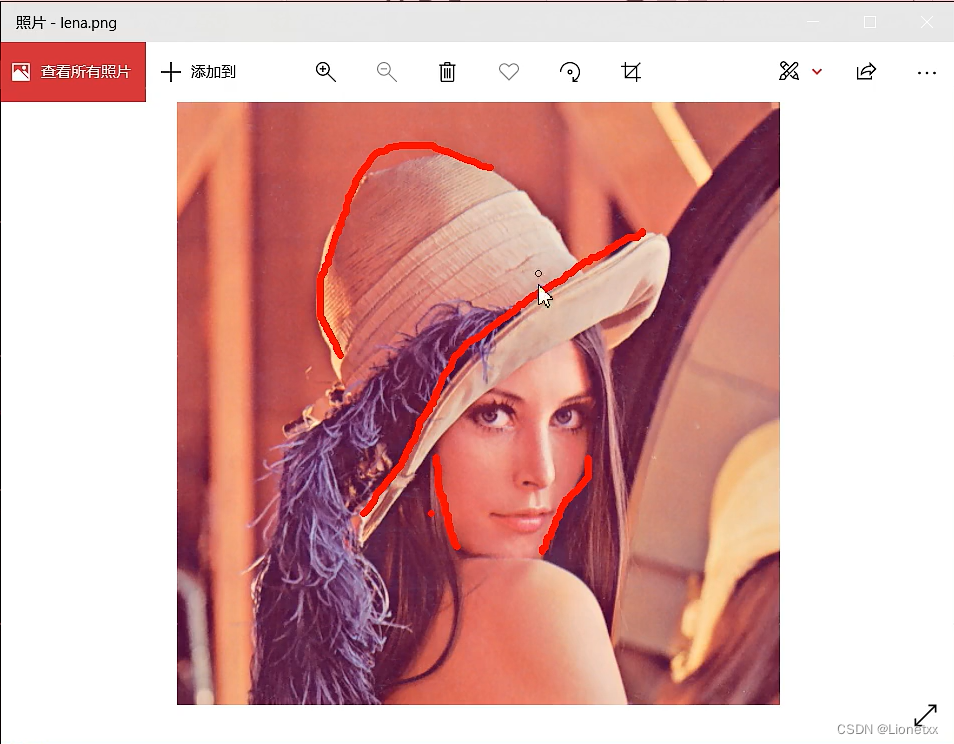
在这里插入图片描述

对于高斯滤波，仅用空间距离的权值系数核（卷积核）与图像卷积后，确定中心点的灰度值。即认为：离中心越近的点，其权重系数越大

双边滤波中加入了对灰度信息的权重，即在邻域内，灰度值越接近中心点灰度值的点，其权重更大，灰度值相差越大的点权重越小

两者权重系数相乘，即得到最终的卷积模板。由于双边滤波需要每个点的中心点邻域的灰度信息来确定其系数，所以其速度比一般的滤波慢得多

（乘积第一项为高斯滤波的函数；第二项为灰度值滤波的函数；Iq为该点的像素值）

我们可以发现灰度值变化十分明显，是垂直的下降。二者叠加后，右边还是正常地进行高斯滤波，左边；左边由于灰度值相差太大，相当于被拉低了，原来是怎么样现在还是怎么样

美颜效果的原因：双边滤波会保留边缘信息，而把非边缘的信息进行高斯滤波处理，相当于磨皮了（模糊化）

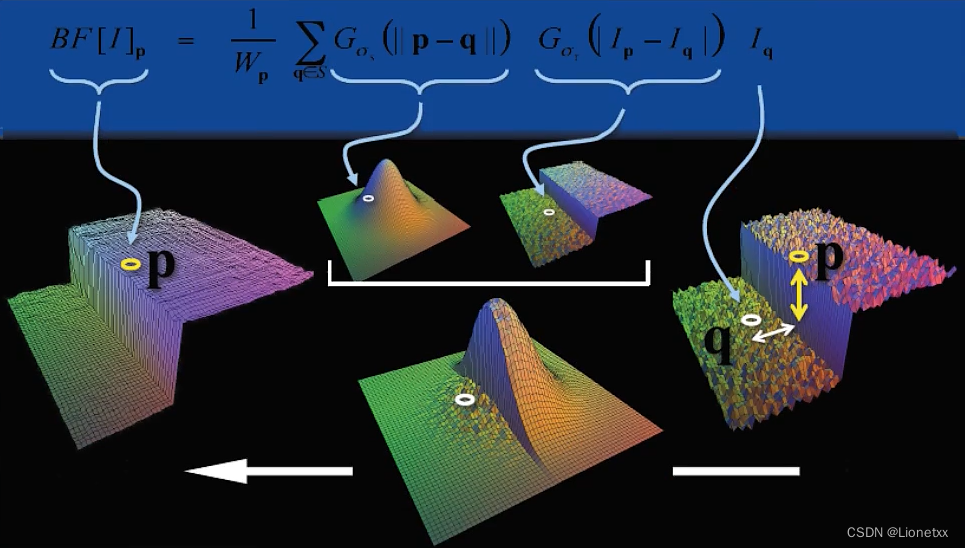
在这里插入图片描述

关键API：cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])
其中：

src：原图
d：卷积核大小，写整数即可！
sigmaColor：计算“灰度距离”时使用的σ
sigmaSpace：计算“空间距离”时使用的σ

import cv2
import numpy as np

img = cv2.imread('./lena.jpeg')

dst = cv2.bilateralFilter(img,7,sigmaColor = 20,sigmaSpace = 40)

cv2.imshow('img',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
可以发现有很明显的美颜效果

我们逐渐减小卷积核的大小d，会发现效果越来越差
在这里插入图片描述

我们试着用双边滤波来处理椒盐噪声
在这里插入图片描述
可以发现毫无作用：由于椒盐噪声的灰度值变化大，而双边滤波只对两边进行优化，不对边缘进行处理，但噪声的周围都是白色的呀，没啥好优化的，因此无效果

前面所将的滤波都是用来把噪声消除，进行降噪操作的 ——> 我们一般称为低通滤波

我们现在所讲的算子则是用来找边界的（用于识别图像的边缘） ——> 我们一般称为高通滤波

算子

注意：我们的结果都是黑白的，因为是用灰度值进行计算；且无法还原，因为我们是为了找到图像的边缘而进行的灰度值处理，在计算时就改变了颜色

索贝尔（`Sobel`）算子

Sobel：边缘检测滤波器

边缘是像素值发生跃迁的位置，是图像的显著特征之一，在图像特征提取、对象检测、模式识别等方面都有重要作用

人眼如何识别图像边缘？

比如有一幅图，图里有一条线，左边很亮，右边很暗，那么人眼就很容易以这条线为边缘，也就是像素灰度值快速变化的地方

Sobel算子对图像求一阶导数：一阶导数越大，说明像素在该方向上的变化越大，边缘信号越强

因为图像的灰度值都是离散的数字，Sobel算子采用离散差分算子计算图像像素点亮度值的近似梯度

在这里插入图片描述

离散差分算子：假如该点的灰度值为180，那么我们对灰度值=180的的这个点进行求导，如果向前求导，假如移动2个单位：k = ( f(180) - f(180 + 2) ) / 2

图像是二维的，即沿着宽度/高度两个方向，因此我们分开计算水平梯度和垂直梯度

我们使用两个卷积核对原图像进行处理

（其实整个环节是环环相扣的：边缘是像素值变化较快的地方 ——> 怎么把像素值变化快的地方找出来 ——> 对图像求导 ——> 可图像都是离散的数字，怎么求导 ——> 数学上使用离散差分算子 ——> 求f(x)的导数：给他加一点、减一点 ——> 我们就通过下方的两个卷积核模拟加一点、减一点的过程
在这里插入图片描述

这样的话，我们就得到了一个新的矩阵：分别反映每一点的像素在水平方向上的亮度变化情况和在垂直方向上的亮度变化情况

综合考虑这两个方向的变化，我们使用以下公式反映某个像素的梯度变化情况

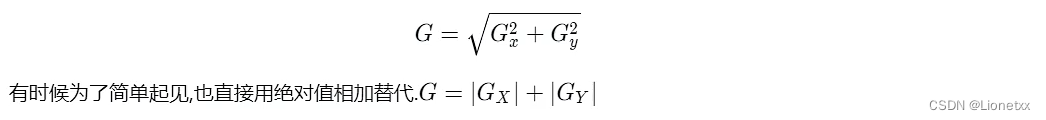
在这里插入图片描述

关键API：Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]])
其中：

src：原图
ddepth：位深，即图片的数据类型，一般我们写-1即可，也可以写opencv自己的写法（如64位float型数据cv2.CV_64F）
dx、dy：如果你指定了dx（且dy = 0），就表示要计算x轴（水平方向）的梯度；如果你指定了dy（且dx = 0），就表示要计算y轴（竖直方向）的梯度
- 注意：我们的Sobel算子要分开计算x、y轴的梯度dx、dy
dst：我们输出图片的结果，一般不用写，只需要在函数前写一个值接受即可
ksize：Sobel的卷积核大小，只能够写一个数！且为奇数！

结果：
我们先看看dx的效果
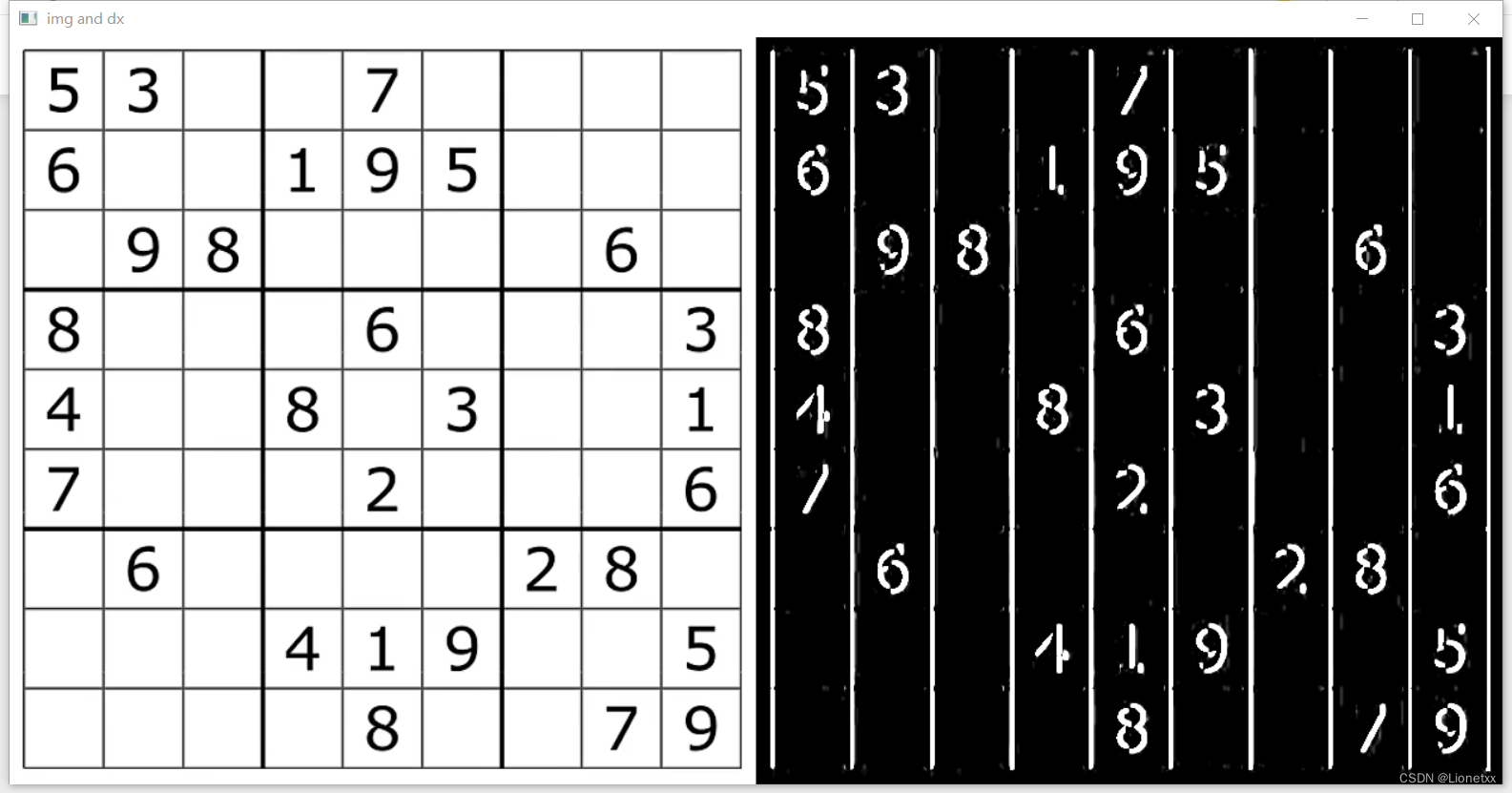
在这里插入图片描述
我们可以发现水平方向的直线都被抹掉了（我们求的是dx水平方向，结果显示出来的全是竖直方向的边缘）

因为我们计算水平方向时，使用后面的一竖列 - 前面的竖列，算出来的东西就是垂直的东西；垂直方向同理，对垂直方向计算梯度，垂直方向没了，只剩下行
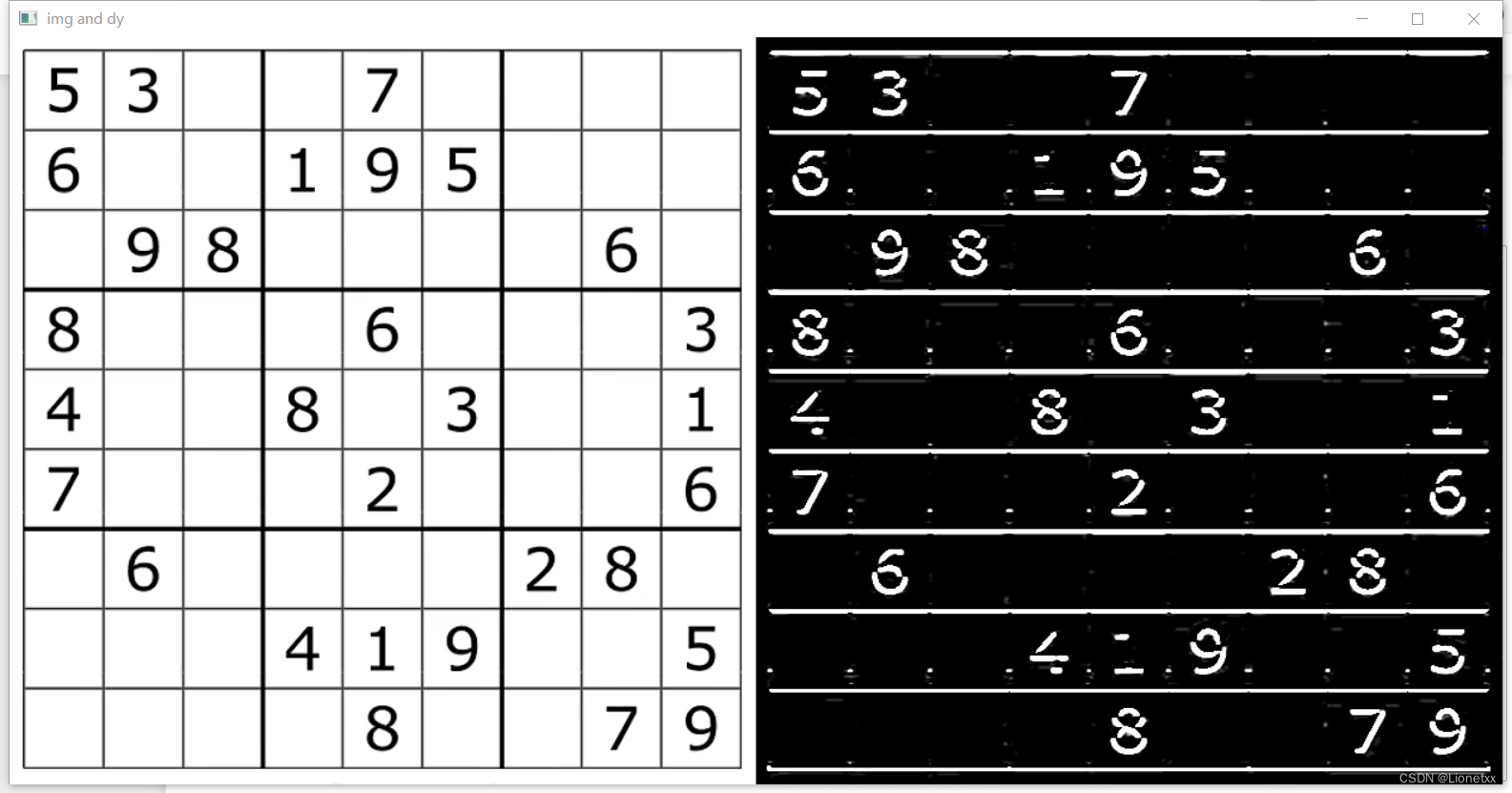
在这里插入图片描述

dy的效果：

在这里插入图片描述

我们可以发现竖直方向的直线都被抹掉了（我们求的是dy竖直方向，结果显示出来的全是竖直方向的边缘）

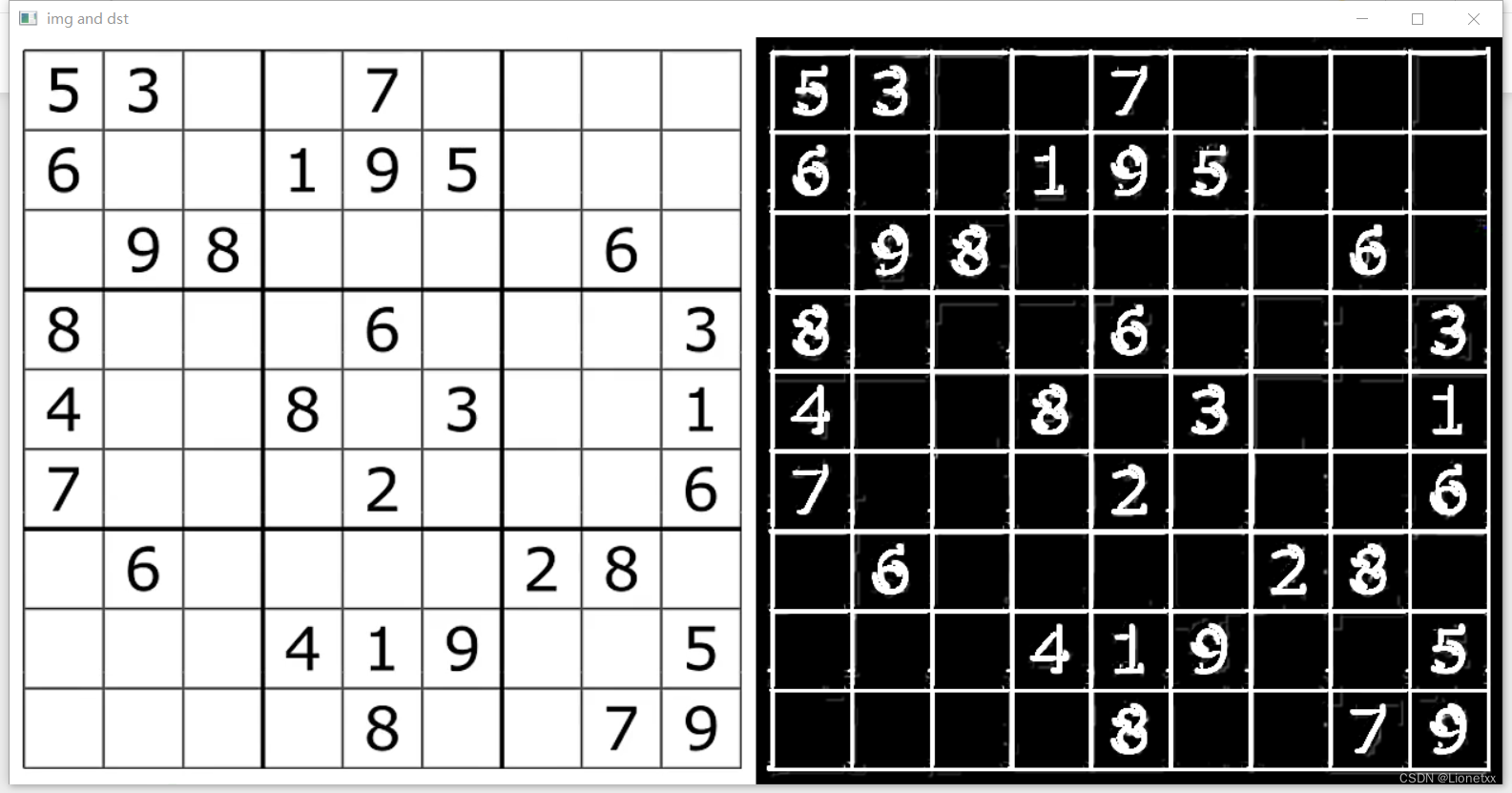
我们要得到一个完整的效果，只需要把两个图片合在一起即可！

关键API：cv2.add(dx,dy) 因为图片格式为 .png，都是正数，直接加起来即可

在这里插入图片描述

沙尔（`Scharr`）算子

沙尔算子是对索贝尔算子的提升

当卷积核大小为3时，以上Sobel内核可能产生比较明显的误差 （毕竟Sobel算子只是求取了导数的近似值），为了解决这一问题，OpenCV提供了Scharr函数，但该函数仅作用于大小为3的卷积核。该函数的运算速度与Sobel一样快，但结果却更加准确
Scharr算子和Sobel算子很类似，只不过使用了不同的卷积核kernel中的值，放大了像素变化情况

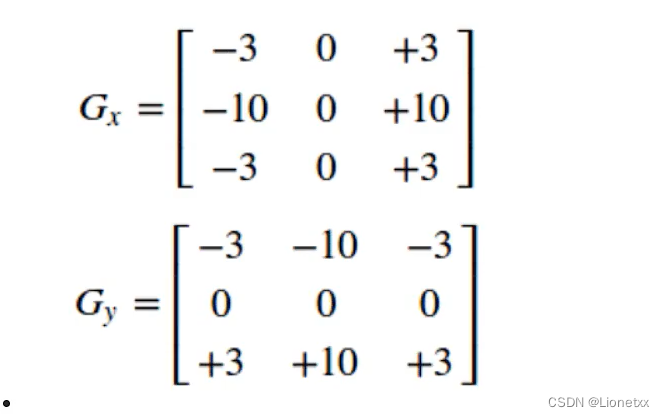
在这里插入图片描述

关键API：Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]])
其中：

Scharr算子只支持3*3的卷积核kernel，所以没有kernel参数
Scharr算子只能求x方向或y方向的边缘
Sobel算子的ksize设置成-1就是Scharr算子
Scharr算子一般适用于寻找细小的边缘，用的比较少

结果：

原图：

在这里插入图片描述

效果：

dx dy dst
dx只看得到垂直的东西
dy只看得到水平的东西

我们可以发现一些细小的边缘（头发丝、帽檐...）都能被展示出来

在这里插入图片描述

对比索贝尔Sobel算子
在这里插入图片描述
明显发现是沙尔算子（Scharr）效果好

拉普拉斯（`Laplacian`）算子

拉普拉斯（Laplacian）算子则又是在沙尔算子的基础上进化出来的

索贝尔Sobel算子是模拟一阶求导，导数越大的地方说明变换越剧烈，则越有可能是边缘

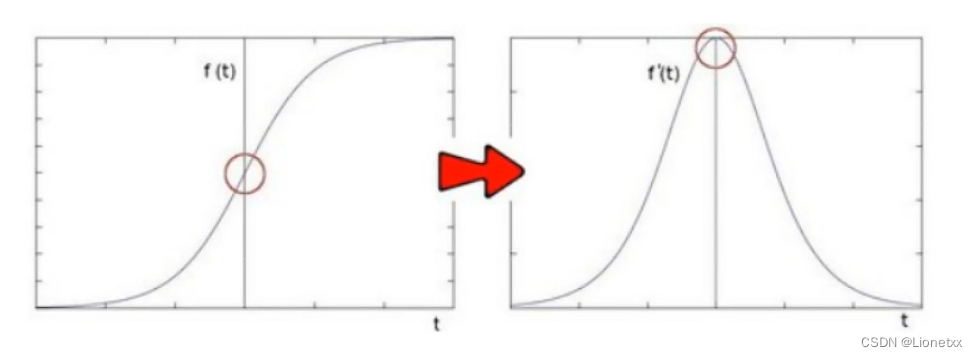
在这里插入图片描述
那如果继续对f'(x)求导呢

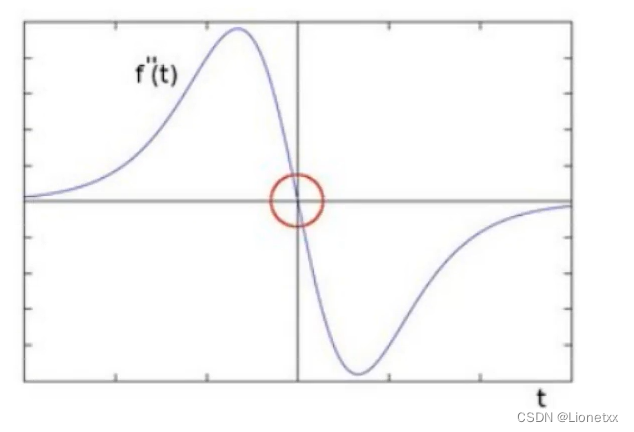
在这里插入图片描述

可以发现边缘处的二阶导数=0，我们可以利用这一特性去寻找图像的边缘，注意有一个问题：二阶求导为0的位置也可能是无意义的位置，这些位置一般都是噪声，因此如果我们用拉普拉斯（Laplacian）算子时可能需要用到高斯滤波进行降噪

拉普拉斯（Laplacian）算子的推导

两个矩阵中间的算术运算符表示两个矩阵的对应点相乘

即类比于索贝尔算子和沙尔算子，拉普拉斯（Laplacian）算子的卷积核为：
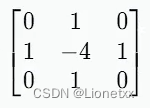
在这里插入图片描述

关键API：Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

可以同时求两个方向的边缘，即不用再像上面两种算子要把dx、dy分开来求
对噪声敏感，一般需要进行降噪后再调用拉普拉斯算子

import cv2
import numpy as np

img = cv2.imread('./chess.png')

dst = cv2.Laplacian(img,-1)

# 观察
cv2.imshow(' dx dy dst ',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
在这里插入图片描述

拉普拉斯算子处理椒盐噪声

我们试着用拉普拉斯算子来处理充满椒盐噪声的图：

import cv2
import numpy as np

# img = cv2.imread('./chess.png')
img = cv2.imread('./papper.png')


dst = cv2.Laplacian(img,-1,ksize = 5)

# 观察
cv2.imshow(' dx dy dst ',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

结果：
在这里插入图片描述
可以发现噪声反而更加吗明显了！我们可以先用中值滤波降噪，再使用拉普拉斯算子：

# 拉普拉斯算子处理椒盐噪声
# 先降噪，后进行拉普拉斯算子运算

import cv2
import numpy as np

# img = cv2.imread('./chess.png')
img = cv2.imread('./papper.png')

# 进行中值滤波——> 降噪处理
temp = cv2.medianBlur(img,7)

# 进行拉普拉斯算子运算
dst = cv2.Laplacian(temp,-1,ksize = 5)

# 观察
cv2.imshow(' dx dy dst ',np.hstack((img,dst)))

cv2.waitKey(0)
cv2.destroyAllWindows()

在这里插入图片描述

边缘检测`Canny`

Canny边缘检测是边缘检测算法中的最优算法，最优边缘检测的三个主要评价标准是：

低错误率： 标识出尽可能多的实际边缘，同时尽可能减少噪声的误报
高定位性： 标识出的边缘要与图像中的边缘尽可能接近
最小响应： 图像中的边缘只能标识一次

Canny边缘检测的一般步骤：

去噪： 边缘检测容易受到噪声影响，在进行边缘检测前一般要进行去噪，一般用高斯滤波去除噪声
计算梯度： 对平滑后的图像采用索贝尔（Sobel）算子计算梯度dx、dy和方向dy/dx（采用Sobel算子的原因是因为）

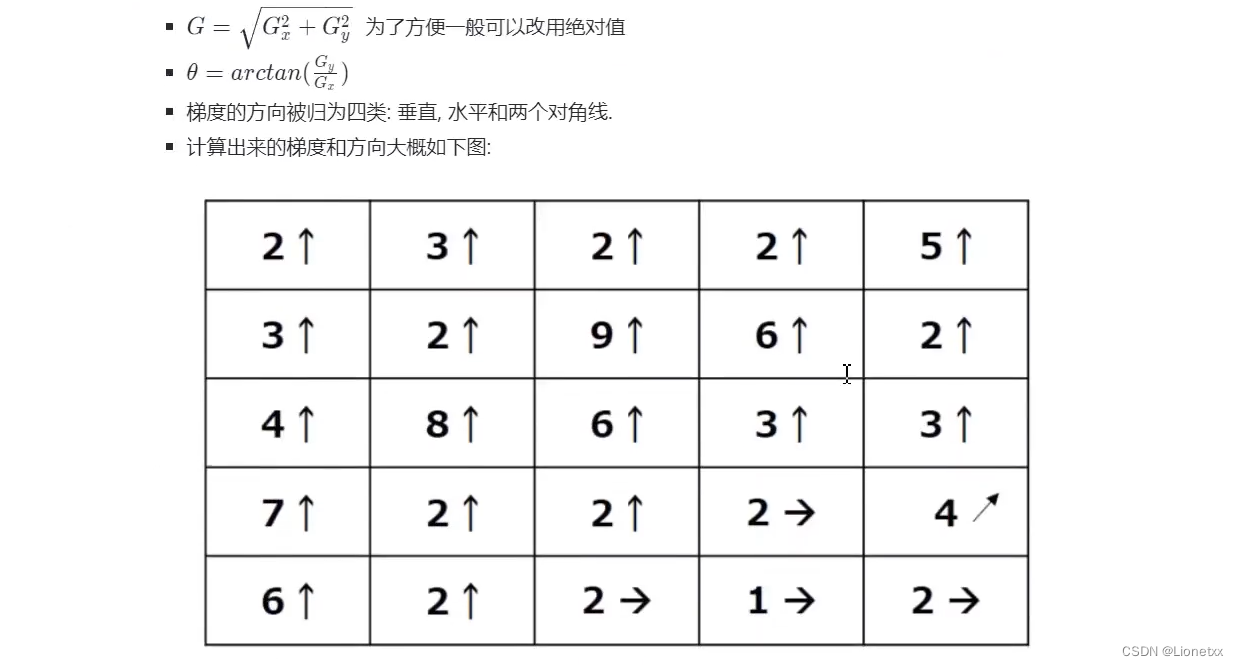
非极大值抑制（NMS算法）：

在获取了梯度和方向后，遍历图像，去除所有不是边界的点
实现方法：逐个遍历像素点，判断当前像素点是否是周围具有相同方向梯度的像素点中的“最大值”
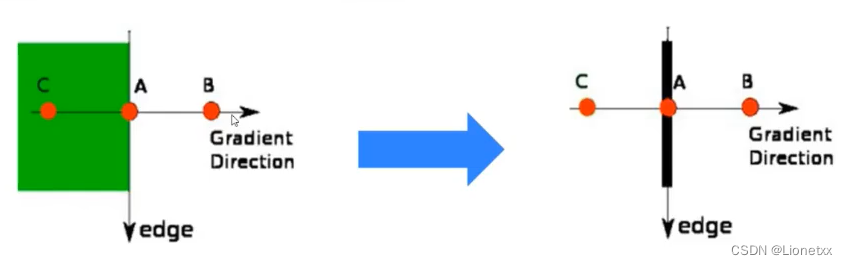
下图中：点A、B、C具有相同的方向（水平向右：Gradient Direction 梯度方向），梯度方向垂直于边缘
判断点A是否为A、B、C中的局部最大值：如果是，保留该点；否则，它被抑制（归零）
更形象的例子

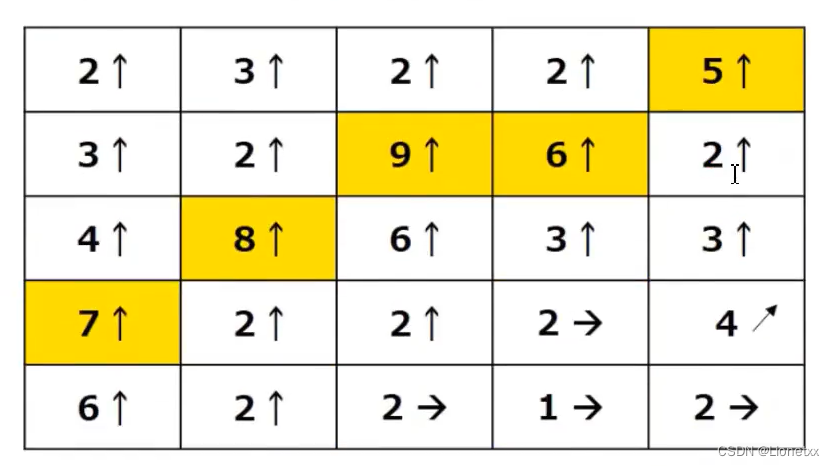
第一列：7最大，取7，其他的都归零舍去；第三列：向上的梯度方向占多数，因此不管向右的梯度方向，取最大的9，其余归零
滞后阈值：它会设定两个阈值maxVal和minVal
- 如果我们刚刚算出该点的梯度值 > maxVal，则该点一定是边缘像素点，如点A；
- 如果我们刚刚算出该点的梯度值 < maxVal，则该点一定不是边缘像素点，抛弃掉，如点D
- 如果minVal < 梯度值 < maxVal：如果该点与边界（点A）相连，则保留，如点C；如果该点与边界不相连，则抛弃，如点D

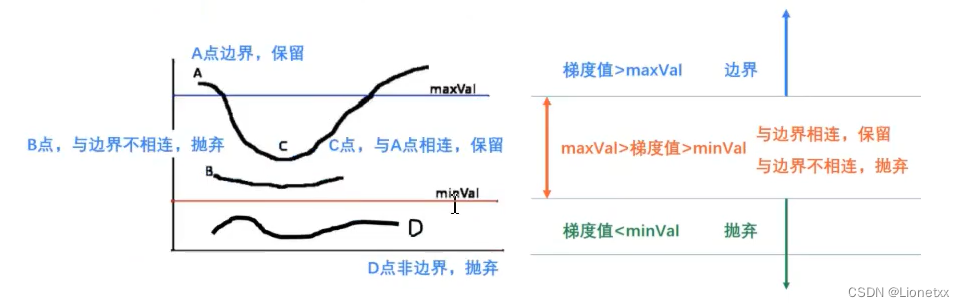
怎么判断是否相连：在上方的方格图中相邻位置的点即相连

关键API：Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]])
其中：

image：进行边缘检测的图片
threshold1：最小值
threshold2：最大值

# Canny
import cv2
import numpy as np

# 导入图片
img = cv2.imread('./lena.png')

# 利用Canny边缘算法
dst1 = cv2.Canny(img,100,200)  # 阈值给的稍大一些，绘制的边缘不够精细
dst2 = cv2.Canny(img,70,150)  # 可以通过给小一点阈值，得到较为精细的边缘



# 观察
# cv2.imshow(' img and dst ',np.hstack((img,dst)))    # 不能和原图一起展示！我们检测边缘时会把图像变成二维（灰度图），和原图格式不一样！
cv2.imshow('threshold:Left > Right ',np.hstack((dst1,dst2)))


cv2.waitKey(0)
cv2.destroyAllWindows()