lesson8 deep learnin from the foundations 从基础开始
- Jupyter notebook:
- 01_matmul.ipynb
- 02_fully_connected.ipynb
- lesson8 notes :https://github.com/HaronCHou/deeplearning-assignment/blob/master/lesson8/lesson8.md
?0. 前言
- 从基础开始:学习实现fastai和pytorch库的功能。学习构建库的一些方法。
- 重写fastai和pytorch的很多函数:矩阵惩罚、torch.nn,torch.optim,dataloader等
- 深度学习的前言其实是工程上的,而不只是论文。深度学习领域里,优秀的人更有效率,就是他们能用代码做出有用的东西。part2的目的就是让代码能够work。
- why foudations?为什么要从基础开始学习呢?
① 需要真实的实践:了解模型在干什么?训练中真正在发生一些什么?
② understand by creating it。以重构的方式来理解,以debug的方式来理解。 - modern CNN model的步骤
- ① 矩阵乘法
- ② Relu/初始化
- ③ 前向传播
- ④ 反向传播
- ⑤ train loop 训练循环
- ⑥ conv卷积层
- ⑧ 优化 Optim
- ⑨ 批归一化 batch normalization
- ?Resnet
① 矩阵乘法
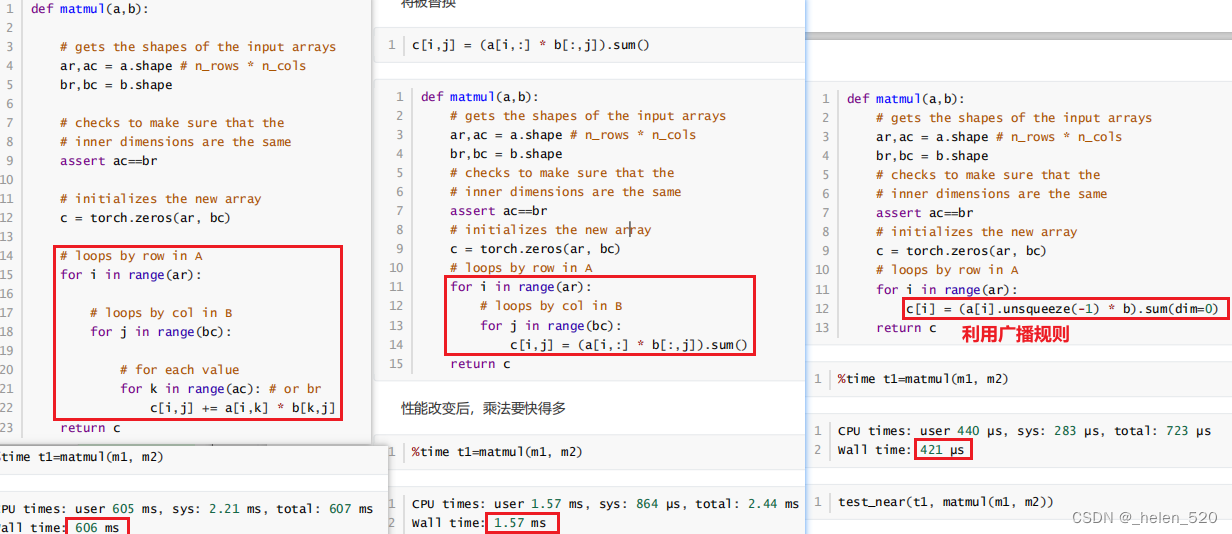
- 第二个使用了pytorch的点乘,利用了torch的点乘;大大加快了速度。
- dim(0)是沿着行;unsqueeze(-1)是沿着列广播;
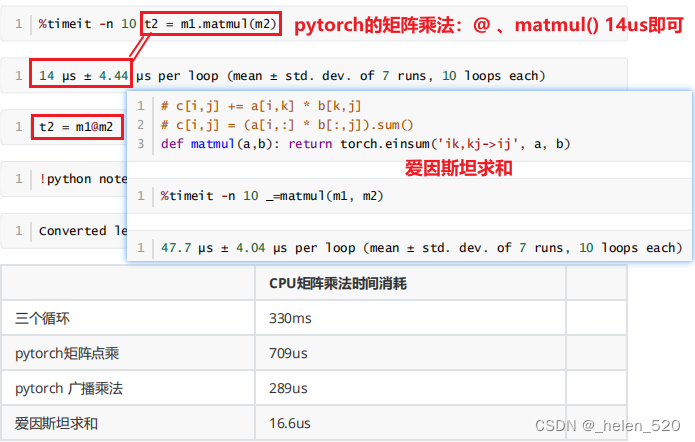
- pytorch的矩阵乘法是最快的;
m1 = x_valid[:5]
m2 = weights
m1.shape, m2.shape
# (torch.Size([5, 784]), torch.Size([784, 10]))
?
?② Relu/初始化——来源于何凯明的ImageNet比赛获奖paper,ReLU、Resnet、kaiming归一化等
第一个简单模型:y=(x*w1+b1)*w2 + b2
- 非卷积层,简单的线性层;sqrt(2/m)*uniform,ReLU(x*w1+b1)后,均值为0.5,方差0.8;
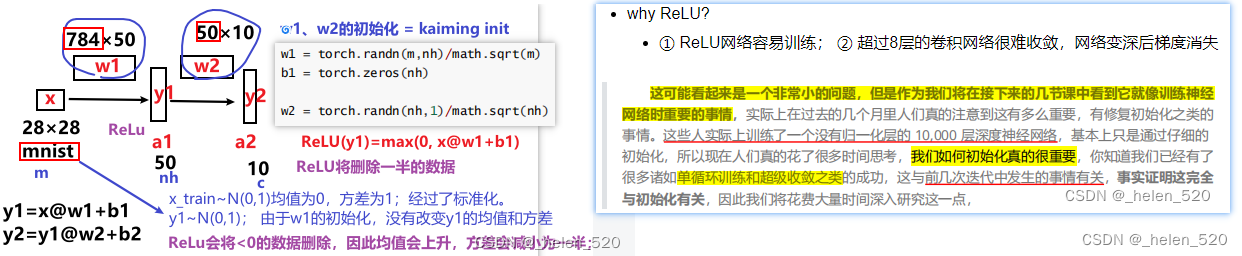
?A。why ReLU?
- ① ReLU网络容易训练; ② 超过8层的卷积网络很难收敛,网络变深后梯度消失
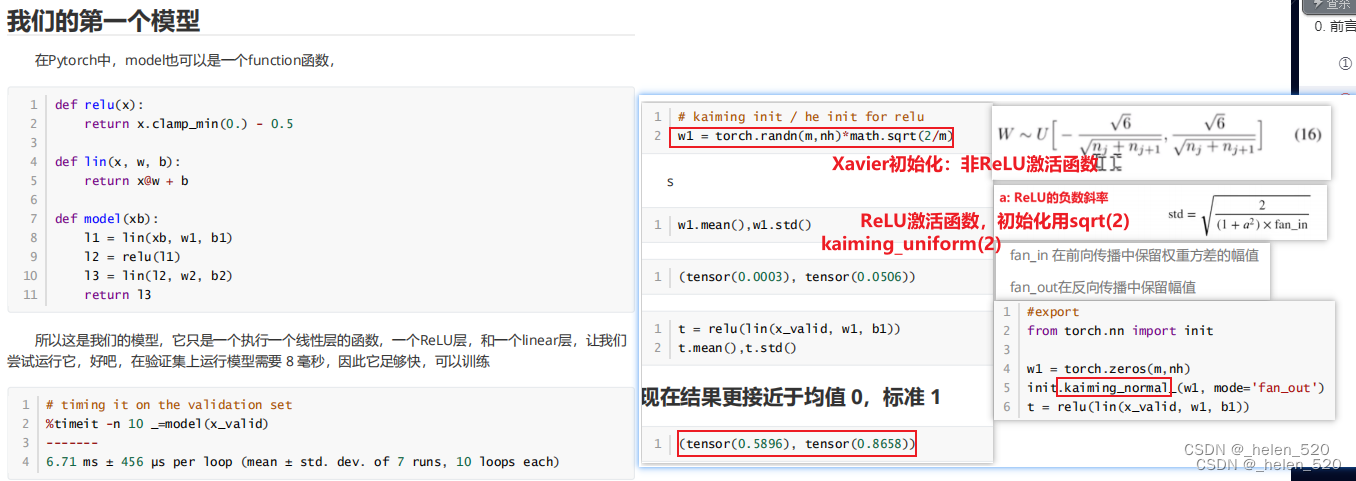
?为什么需要一个好的初始化?why a good init? lesson 9
- fastai 2019 lesson9 notes 笔记__helen_520的博客-CSDN博客
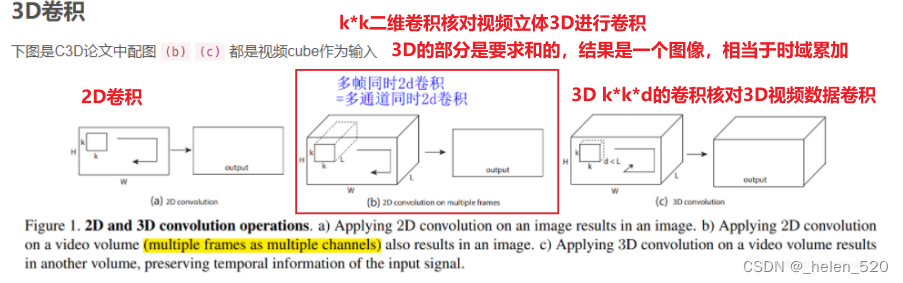
- torch.Conv2d对l1的初始化,是sqrt(5);x经过l1卷积后,均值方差变化了。
- l1.weight == torch.Size([32, 1, 5, 5]) 怎么看待这个滤波器?
- Conv2d的sqrt(5)初始化,让x没经过一次卷积层,方差都减小了;经过4层卷积层后,方差只有0.06了。梯度消失了!!!!
- 怎么样是一个好的初始化?为什么呢?
- D(X)=E(X^2) - E(X)^2。
- E((XY)^2)
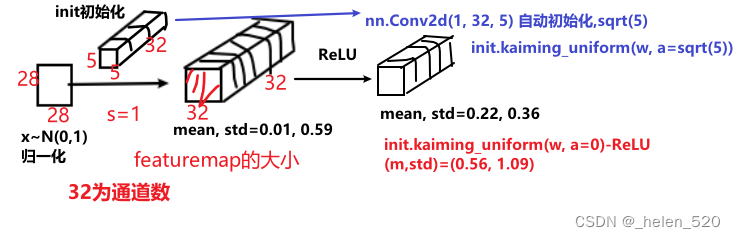
3D卷积的计算方式如下所示:
def get_data():
path = Path('/dataset_zhr/lesson5-sgd-mnist/MNIST dataset/mnist.pkl.gz')
with gzip.open(path, 'rb') as f:
((x_train, y_train),(x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
return map(tensor, (x_train, y_train, x_valid, y_valid)) # 映射为tensor格式
def normalize(x, m, x): return (x-m)/s
# 数据预处理,归一化
x_train, y_train, x_valid, y_valid = get_data() # torch.Size([50000, 784])
train_mean, train_std = x_train.mean(), x_train.std()
x_train = normalize(x_train, train_mean, train_std)
x_valid = normalize(x_valid, train_mean, train_std) # 用train训练集的均值和标准差来归一化valid验证集
x_train = x_train.view(-1, 1, 28, 28)
x_valid = x_valid.view(-1, 1, 28, 28)
x_train.shape # torch.Size([50000, 1, 28, 28])
n, *_ = x_train.shape
c = y_train.max() + 1 # torch.tensor格式,tensor有很多函数,max(), min(), len(y), y.mean等函数都可以直接调用的,具体参考torch.tensor
nh= 50 # num of hidden layers 一个隐藏层
l1 = nn.Conv2d(1, nh, 5) # Conv2d(1, 32, kernel_size=(5,5), stride=(1,1))
l1.weight.shape # torch.Size([50, 1, 5, 5])
t = l1(x) # 输入经过卷积层之后的结果
stats(t)
----------
(tensor(0.0107, grad_fn=<MeanBackward1>),
tensor(0.5978, grad_fn=<StdBackward0>))
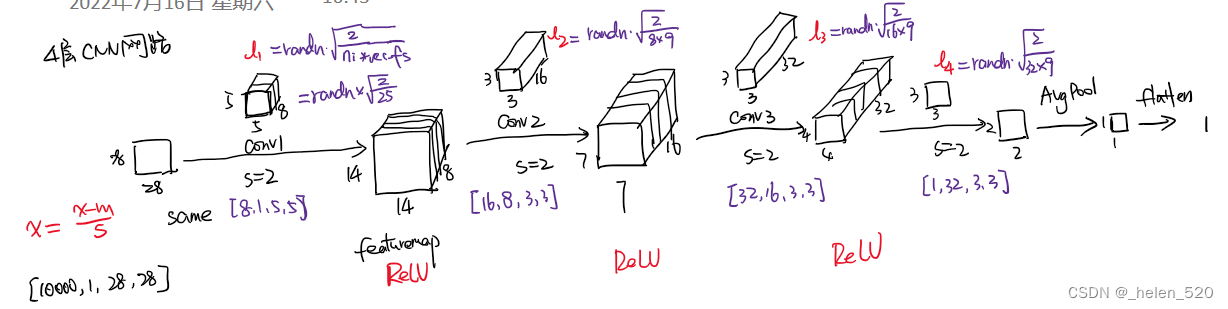
- 4层CNN网络如图所示,正向传播后,x的方差下降的很厉害;
- 误差在反向传播时,grad在m[0]处几乎为0,梯度没有什么变化,梯度消失了。?
- 为什么要sqrt(/m)?ReLU为啥是sqrt(2/m)??scaling的神奇数字。
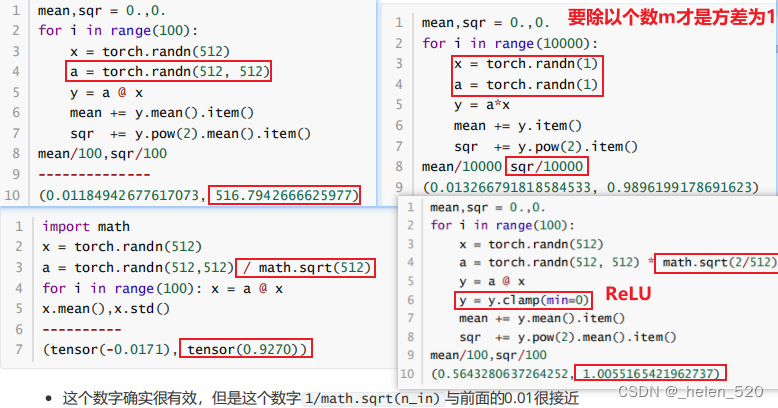
- ????从数学上证明,只要 a 中和 x 中的元素是独立的,均值是 0,std 是 1。
- a*x相乘,m个ax的乘积的和,要除以m,才能保证均值为1;
- 也就是让a在初始化的时候乘以 sqrt(1/m);
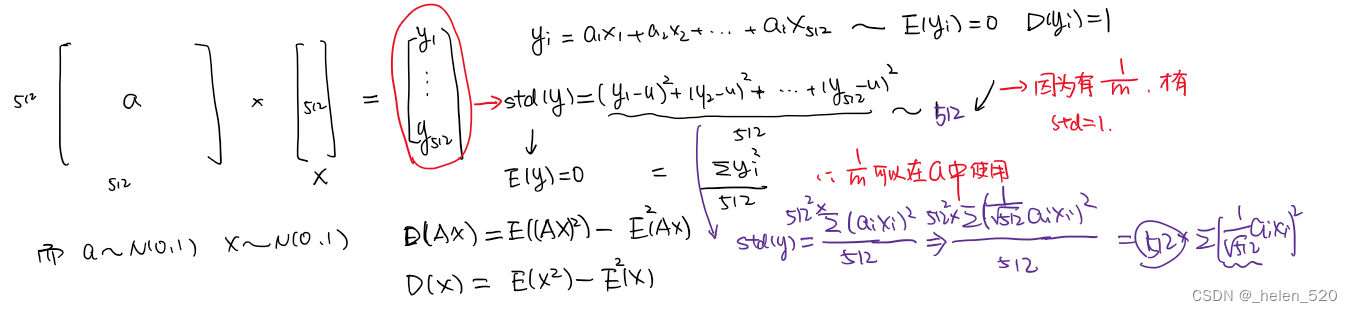
#export
from exp.nb_02 import *
def get_data():
# path = datasets.download_data(MNIST_URL, ext='.gz')
path = Path('/dataset_zhr/lesson5-sgd-mnist/MNIST dataset/mnist.pkl.gz')
with gzip.open(path, 'rb') as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding='latin-1')
return map(tensor, (x_train,y_train,x_valid,y_valid))
def normalize(x, m, s): return (x-m)/s
x_train,y_train,x_valid,y_valid = get_data() # # torch.Size([50000, 784])
train_mean,train_std = x_train.mean(),x_train.std()
x_train = normalize(x_train, train_mean, train_std)
# NB: Use training, not validation mean for validation set
x_valid = normalize(x_valid, train_mean, train_std)
n,m,*_ = x_train.shape
c = y_train.max()+1
""" 一、线性层测试:l1->Relu->l2(10) 一个线性隐藏层(非卷积层)
"""
nh = 50
w1 = torch.randn(m,nh)/math.sqrt(m) # 线性层的初始化方式:Xavier初始化
b1 = torch.zeros(nh)
w2 = torch.randn(nh,1)/math.sqrt(nh)
b2 = torch.zeros(1)
# 状态函数
def stats(x): return x.mean(), x.std()
def lin(x, w, b): return x@w + b
def relu(x): return x.clamp_min(0.)
t = lin(x_valid, w1, b1)
stats(t) # (tensor(0.0988), tensor(1.0425))
stats(relu(t)) # (tensor(0.4659), tensor(0.6480))
# ① ReLU用sqrt(2)初始化,方差保持1
w1 = torch.randn(m,nh)*math.sqrt(2/m)
stats(relu(lin(x_valid, w1, b1))) # (tensor(0.5844), tensor(0.8691))
""" 二、卷积层的初始化影响:kaiming初始化参数的影响
"""
x_train = x_train.view(-1,1,28,28)
x_valid = x_valid.view(-1,1,28,28)
from torch import nn
nh = 32
l1 = nn.Conv2d(1, nh, 5)
stats(l1.weight)
stats(l1(x_valid)) # (tensor(-0.0300, grad...ackward0>), tensor(0.6502, grad_...ackward0>))
""" l1是torch.nn.modules.conv.Conv2d,类本身有__call__函数,所以对象名+括号,l1()直接调用了__call__函数
- __call__在Module类中定义了。即在爷类中定义的call函数
"""
import torch.nn.functional as F
def f1(x, a=0):
return F.leaky_relu(l1(x), a)
# pytorch自定义初始化
stats(f1(x_valid)) # (tensor(0.2334, grad_...ackward0>), tensor(0.4282, grad_...ackward0>))
from torch.nn import init
# kaiming初始化
init.kaiming_uniform_(l1.weight, a=0, mode='fan_in')
stats(f1(x_valid)) # (tensor(0.5017, grad_...ackward0>), tensor(0.8888, grad_...ackward0>))
# receptive field size
rec_fs = l1.weight[0,0].numel() # 5*5
nf,ni,*_ = l1.weight.shape # torch.Size([32, 1, 5, 5])
fan_in = ni*rec_fs
fan_out = nf*rec_fs
def gain(a): return math.sqrt(2.0 / (1 + a**2))
def kaiming2(x,a, use_fan_out=False):
nf,ni,*_ = x.shape
rec_fs = x[0,0].shape.numel()
fan = nf*rec_fs if use_fan_out else ni*rec_fs
std = gain(a) / math.sqrt(fan)
bound = math.sqrt(3.) * std
x.data.uniform_(-bound,bound)
kaiming2(l1.weight, a=0)
stats(f1(x_valid)) # tensor(0.5790, grad_...ackward0>), tensor(1.1068, grad_...ackward0>))
"""
三、四个卷积层,初始化不当导致反向传播时梯度消失
"""
class Flatten(nn.Module):
def forward(self,x): return x.view(-1)
"""
m
Sequential(
(0): Conv2d(1, 8, kernel_size=(5, 5), stride=(2, 2), padding=(2, 2))
(1): ReLU()
(2): Conv2d(8, 16, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(3): ReLU()
(4): Conv2d(16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(5): ReLU()
(6): Conv2d(32, 1, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
(7): AdaptiveAvgPool2d(output_size=1)
(8): Flatten()
)
"""
m = nn.Sequential(
nn.Conv2d(1, 8, 5,stride=2,padding=2), nn.ReLU(), # torch.Size([100, 8, 14, 14])
nn.Conv2d(8, 16, 3,stride=2,padding=1), nn.ReLU(), # torch.Size([100, 16, 7, 7])
nn.Conv2d(16, 32, 3,stride=2,padding=1), nn.ReLU(),# torch.Size([100, 32, 4, 4])
nn.Conv2d(32, 1, 3,stride=2,padding=1), # torch.Size([100, 1, 2, 2])
nn.AdaptiveAvgPool2d(1), # torch.Size([100, 1, 1, 1])
Flatten(), # torch.Size([100])
)
t = m(x_valid)
stats(t)
zz = m[1](x_train); print(stats(zz))
# (tensor(0.3480), tensor(0.8555))
zz = m[3](x_train); print(stats(zz))
# (tensor(0.3480), tensor(0.8555))
zz = m[5](x_train); print(stats(zz))
# (tensor(0.3480), tensor(0.8555))
zz = m(x_train); print(stats(zz))
# (tensor(-0.0067, grad_fn=<MeanBackward0>), tensor(0.0132, grad_fn=<StdBackward0>))
l = mse(t, y_valid)
l.backward()
stats(m[0].weight.grad) # (tensor(0.0109), tensor(0.0375))
stats(m[6].weight.grad)
# (tensor(-0.2138), tensor(0.2431))
stats(m[4].weight.grad)
# (tensor(0.0058), tensor(0.0334))
stats(m[2].weight.grad)
# (tensor(0.0077), tensor(0.0297))
stats(m[0].weight.grad)
# (tensor(0.0109), tensor(0.0375))
-
简单线性模型的反向传播 lesson8
# ------------------------------------------------
def model(xb):
l1 = lin(xb, w1, b1)
l2 = relu(l1)
l3 = lin(l2, w2, b2)
return l3
# torch.nn.modules.conv._ConvNd.reset_parameters
"""
线性模型:一个中间层(没有卷积层的情况下)
"""
def mse(output, targ): return (output.squeeze(-1) - targ).pow(2).mean()
y_train,y_valid = y_train.float(),y_valid.float()
def mse_grad(inp, targ):
# grad of loss with respect to output of previous layer
# inp.g = 2. * (inp.squeeze() - targ).unsqueeze(-1) / inp.shape[0]
inp.g = 2. * (inp.squeeze() - targ).unsqueeze(-1) / inp.shape[0] # mse中有mean,所以需要
def relu_grad(inp, out):
# grad of relu with respect to input activations
# inp.g = (inp>0).float() * out.g
inp.g = (inp > 0).float() * out.g
def lin_grad(inp, out, w, b):
# grad of matmul with respect to input
inp.g = out.g @ w.t()
w.g = (inp.unsqueeze(-1) * out.g.unsqueeze(1)).sum(0)
b.g = out.g.sum(0)
def forward_and_backward(inp, targ):
# forward pass:
l1 = inp @ w1 + b1
l2 = relu(l1)
out = l2 @ w2 + b2
# we don't actually need the loss in backward!
loss = mse(out, targ)
# backward pass:
mse_grad(out, targ)
lin_grad(l2, out, w2, b2)
relu_grad(l1, l2)
lin_grad(inp, l1, w1, b1)
forward_and_backward(x_train, y_train)