[人工智能]深度学习（2020李宏毅）学习记录

1. Regression

1.1 Case Study

• 介绍了回归（也是机器学习）的普遍流程：

  1. 定义 模型 or 函数 集合；
  2. 定义损失函数（Loss Function）评估模型的好坏；
  3. 选择最为符合的模型 or 函数；

• 介绍了梯度下降：

  • 单个参数的梯度下降；
  • 两个参数的梯度下降；
  • 回归问题的 Loss Function 是凸函数，其一定能找到全局最优解；
  • 大部分机器学习问题中会存在多个参数，多个参数的梯度下降容易陷入局部最优解；

1.2 Base Concept

• 模型误差

  • 偏差（Bias）& 方差（Variance）
    • 简单的模型：大 bias & 小 variance；
    • 复杂的模型：小 bias& 大 variance；
  • 欠拟合（Underfitting）
    • 主要来源于 Bias ，体现为模型无法很好的拟合训练样本；
    • 解决：
      • 重新设计模型，为模型引入更多的特征，选择更为复杂的函数；
  • 过拟合（Overfitting）
    • 主要来源于 Variance ，体现为模型过度拟合了训练数据，在测试集上效果较差；
    • 解决：
      • 正则化；
      • 采用更过数据进行训练；

• 验证

  • 交叉验证
    

  • N 折交叉验证
    

1.3 Gradient Descent

• Learning Rate 存在的问题

  • 过小：可能能够达到 Loss 最小值点，但完成的时间过长，无法接受；
  • 过大：可能永远无法达到 Loss 最小值点，一直在最小值点的某个范围内振荡 or Loss 会不断增大；

• Adaptive Learning Rate

  • Adagrad
    • 将不同参数的learning rate分开考虑的一种算法；
      
  • Stochastic Gradicent Descent
    • 随机梯度下降的?法可以让训练更快速，传统的gradient descent的思路是看完所有的样本点之后再构建loss function，然后去update参数；?stochastic gradient descent的做法是，看到?个样本点就update?次，因此它的loss function不是所有样本点的error平?和，?是这个随机样本点的error平?；
      
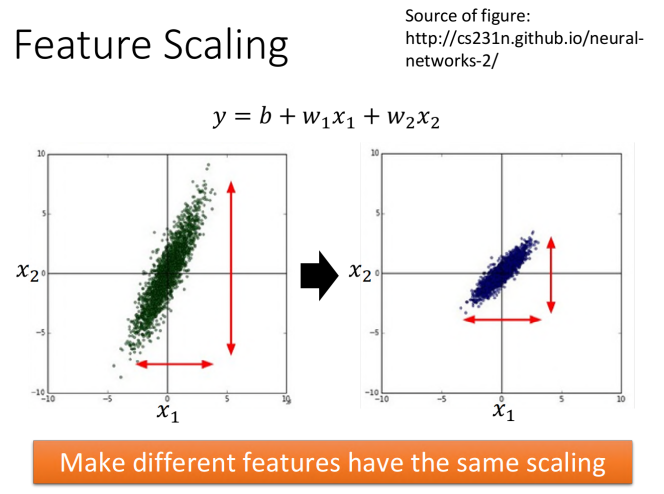
  • Feature Scaling
    • 特征缩放，当多个特征的分布范围很不?样时，最好将这些不同feature的范围缩放成?样；
    • 本质上就是将每?个参数都归?化成标准正态分布；
      

• Gradient Descent的限制

  • 在gradient即微分值接近于0的地?就会停下来，?这个地?不?定是global minima，它可能是local minima，可能是saddle point鞍点，甚?可能是?个loss很?的plateau平缓?原；