基于logistic回归的分类模型:
- 对于二分类模型,采用基础逻辑回归(logistic regression)
- 对于多分类模型,采用多分类逻辑回归
逻辑回归的要求(针对01)
假设1:因变量(结局)是二分类变量。
假设2:有至少1个自变量,自变量可以是连续变量,也可以是分类变量。
假设3:每条观测间相互独立。分类变量(包括因变量和自变量)的分类必须全面且每一个分类间互斥。
假设4:最小样本量要求为自变量数目的15倍,但一些研究者认为样本量应达到自变量数目的50倍。
假设5:连续的自变量与因变量的logit转换值之间存在线性关系。
假设6:自变量之间无多重共线性。
假设7:没有明显的离群点、杠杆点和强影响点。
ps. 如何检验假设5-7,并进行Logistics回归
参考: 二分类logistic回归,更新几个常见问题的解决方法
所要解决的问题
逻辑回归的结果一般用于估计某种事物的可能性(“可能性”,而非数学上的“概率”),不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和,而非直接相乘。
逻辑回归可以用于预测在给定的过程中,系统或产品的故障的可能性。还用于市场营销应用程序,例如预测客户购买产品或中止订购的倾向等。在经济学中它可以用来预测一个人选择进入劳动力市场的可能性,而商业应用则可以用来预测房主拖欠抵押贷款的可能性。则可以根据logistic回归模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大。最初由Boyd 等人开发的创伤和损伤严重度评分(TRISS)被广泛用于预测受伤患者的死亡率,使用逻辑回归 基于观察到的患者特征(年龄,性别,体重指数,各种血液检查的结果等)分析预测发生特定疾病(例如糖尿病,冠心病)的风险。
逻辑回归模型现在同样是很多分类算法的基础组件。
逻辑回归原理
逻辑回归一种广义线性回归模型,逻辑回归假设因变量 y 服从伯努利分布,在线性回归基础上利用Sigmoid映射函数来实现。其主要用于分类。它在线性回归的基础上加入了sigmoid函数,将线性回归的结果输入至sigmoid函数中,并且设定一个阈值,如果大于阈值为1,小于阈值为0。通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
标准线性回归:
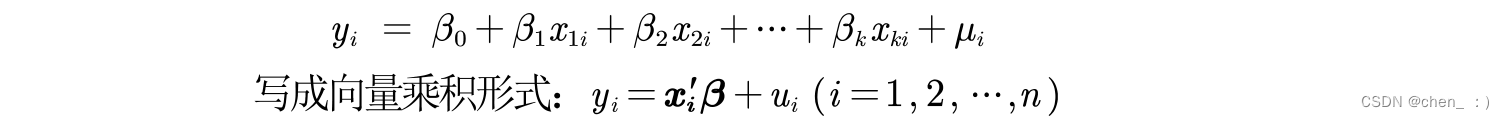
logistic回归:

 核心函数:
核心函数:
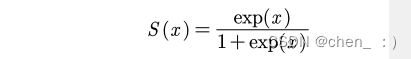
具体推导过程:
机器学习算法(二)逻辑回归的原理和实现
逻辑回归原理解释
二元逻辑回归
1. 使用场景

2. 使用方法
利用Spss软件
操作:
Analyze→Regression→Binary Logistic
具体使用方法:
SPSS操作方法:逻辑回归
输出结果分析:
logistic回归分析优点_SPSS统计分析全解析Logistic回归(逻辑回归)
多元逻辑回归
核心: Sigmoid函数 推广为 Softmax函数
Softmax回归——logistic回归模型在多分类问题上的推广
1. 使用场景
在实际应用中,可能还会碰到因变量是多个分类的情况,并且不包含排序信息
2. 使用方法
注意,这里要将几个自变量放到协变量中。
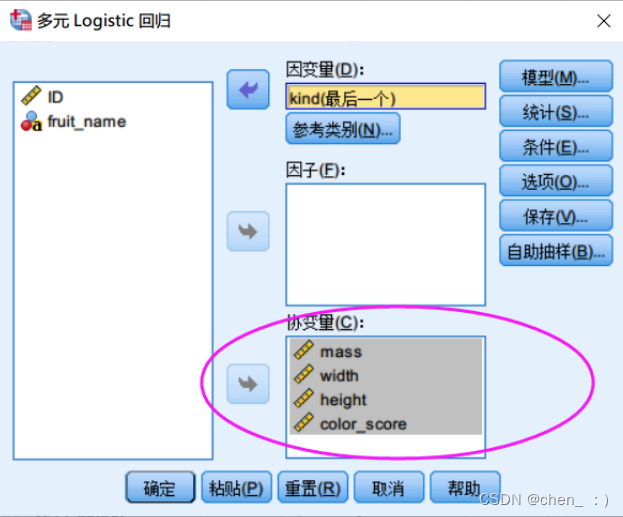
Spss中因子和协变量的区别
因子指分类型变量,例如性别、学历等
协变量指连续型变量,例如面积、重量等
多因素logistic回归分析spss步骤:打开数据,依次点击:analyse–regression–binarylogistic,打开二分回归对话框
注意事项
a. 交互项的影响
如果想要进行交互作用的分析,同时选中两个自变量,将两个变量的交互作用项选入方程来进行分析。
b.如何确定合适的模型
把数据分为训练组和测试组,用训练组的数据来估计出模
型,再用测试组的数据来进行测试。(训练组和测试组的比
例一般设置为80%和20%)
(注意:为了消除偶然性的影响,可以对上述步骤多重复几次,最
终对每个模型求一个平均的准确率,这个步骤称为交叉验证。)
可在logistic回归模型中加入平方项、交互项等。
c. 分类变量的转化
两种方法
(1)先创建虚拟变量,然后删除任意一列以排除完全多重共线性的影响;
(2)直接点击分类,然后定义分类协变量,Spss会自动帮我们生成。
(如果没有生成虚拟变量这个选项,则说明SPSS没有安装到默认位置)
d. 逐步回归的设置
向前(向后)逐步回归可选择的统计量有所区别。
进入(或者除去)自变量的显著性水平可以自己调节。
c. 连续的自变量与因变量的logit转换值之间存在线性关系
可用Box-Tidwell法检验连续的自变量与因变量的logit转换值之间是否存在线性关系,即将连续自变量与其自然对数值的交互项纳入回归方程。
e. 样本要求
- 进行logistic回归分析要求样本量最少要为自变量个数的10-15倍
- 对于自变量是定量资料的情况,模型参数的实际意义往往不够明确,最好将其按变量值分成几组再进行logistic回归分析。
f. 过拟合现象

h. 多重共线性
与线性回归一样,Logistic回归模型也需要检验自变量之间是否存在多重共线性。自变量之间的简单相关或多重相关都会产生多重共线性。
容忍度(Tolerance)或方差膨胀因子(VIF)可以用来诊断自变量之间的多重共线性。
如果容忍度(Tolerance)小于0.1或方差膨胀因子(VIF)大于10,则表示有共线性存在。本例中,容忍度均远大于0.1,方差膨胀因子均小于10,所以不存在多重共线性。如果数据存在多重共线性,则需要用复杂的方法进行处理,其中最简单的方法是剔除引起共线性的因素之一,剔除哪一个因素可以基于理论依据。
i. 检测没有明显的离群点、杠杆点和强影响点
j. 对于输出警告的解读

如果遇到了该警告,说明我们的数据中自变量之间存在多重共线性,或者样本中某些类别的观测值较少。
由于我们使用多元逻辑回归是出于分类的目的,因此我们重点因关注分类预测的准确度,这个警告可以忽略。

这个警告说明我们的数据区分度非常高,存在准完全分隔说明样本划分的比较彻底,这一般对于分类结果而言是好事情。
k. 预处理问题
在进行二分类Logistic回归(包括其它Logistic回归)分析前,如果样本不多而变量较多,建议先通过单变量分析(t检验、卡方检验等)考察所有自变量与因变量之间的关系,筛掉一些可能无意义的变量,再进行多因素分析,这样可以保证结果更加可靠。
即使样本足够大,也不建议直接把所有的变量放入方程直接分析,一定要先弄清楚各个变量之间的相互关系,确定自变量进入方程的形式,这样才能有效的进行分析。
详细见:
二分类logistic回归,更新几个常见问题的解决方法
模型的评价
1. 模型整体评价
a. 模型系数的综合检验(Omnibus Tests of Model Coefficients):
Omnibus Tests of Model Coefficients是模型系数的综合检验。其中Model一行输出了Logistic回归模型中所有参数是否均为0的似然比检验结果。P<0.05表示本次拟合的模型中,纳入的变量中,至少有一个变量的OR值有统计学意义,即模型总体有意义。
b. Hosmer and Lemeshow Test
Hosmer and Lemeshow Test是检验模型的拟合优度。当P值不小于检验水准时(即P>0.05),认为当前数据中的信息已经被充分提取,模型拟合优度较高。
c. Model Summary表格
Model Summary表格中,提供了因变量的变异能够被拟合的模型解释的比例。该表格包含Cox & Snell R Square和Nagelkerke R Square,这两种R2有时被称为伪R2,在Logistic回归中意义不大(与线性回归中的不同),可以不予关注。
2. 模型预测能力
对于每一个自变量组合,均可以得到结局事件发生的概率。
如果事件发生的概率大于或等于0.5,Logistic回归判断为事件发生;如果可能性小于0.5,则判断为事件未发生。
因此,与真实情况相比,就可以评价Logistic回归模型的预测效果。
Variables in the Equation表格:
列出了所有自变量及其参数。其中Sig.一列表示相应变量在模型中的P值,Exp (B)和95% CI for EXP (B)表示相应变量的OR值和其95%可信区间。
参考资料
机器学习算法: 逻辑回归的介绍和应用
机器学习算法(二)逻辑回归的原理和实现
逻辑回归原理解释
SPSS操作方法:逻辑回归
logistic回归分析优点_SPSS统计分析全解析Logistic回归(逻辑回归)
Softmax回归——logistic回归模型在多分类问题上的推广
多因素logistic回归分析spss步骤
二分类logistic回归,更新几个常见问题的解决方法 import